Лабораторная работа № 13. Дифференциальные уравнения первого порядка.

I. Краткие теоретические сведения.

1.1. Понятие дифференциального уравнения.

Задачи, приводящие к понятию дифференциального уравнения.

Задача 1. Пусть задана производная некоторой функции у¢=f(x). По заданной производной найти функцию у(х).

З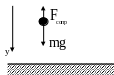 адача 2. Пусть с некоторой высоты h на землю падает тело массой m. Найти закон зависимости скорости падения тела от времени. То есть найти функцию v=v(t).

Решение.

По II закону Ньютона: . ma=mg-F_сопр.

; F_сопр=kv, где к– коэффициент сопротивления воздуха. Тогда .

Задача 3. Распад радиоактивного вещества. Экспериментальным путем была установлена формула зависимости распада радиоактивного вещества: , где m(t) – масса нераспавшегося в момент времени t вещества, a – коэффициент, зависящий от вещества, – скорость распада вещества.

Полученные в задачах 1-3 уравнения наряду переменными содержат производные некоторых функций. Такие уравнения называют дифференциальными.

Определение. Дифференциальными уравнениями (далее – ДУ) называют уравнения, в которые наряду с переменными входят неизвестные функции, а также производные этих функций.

Если неизвестная функция есть функция одной переменной, то такие ДУ называют обыкновенными ДУ; если неизвестная функция есть функция многих переменных, тогда такие ДУ называют ДУ в частных производных.

Далее будем изучать только обыкновенные ДУ и называть их дифференциальными уравнениями.

Определение. Порядок наивысшей производной, входящей в ДУ называется порядком ДУ.

В общем виде ДУ n–го порядка записывают в виде: F(x,y,y¢,…,y⁽ⁿ⁾)=0, (1) причем х,у,у¢,…,у^(n-1) могут и не входить в это уравнение.

Определение. Решением ДУ (1) называется такая функция, которая при подстановке в ДУ обращает его в тождество.

Например. Решение ДУ у¢=f(x) задачи 1 является функция .

Решение ДУ задачи 2 является функция .

Решение ДУ задачи 3 является функция m(t)=-aCe^-at.

Замечание. Решением ДУ n-го порядка может быть только n раз дифференцируемая функция.

В том случае, если уравнение (1) можно представить в виде y⁽ⁿ⁾=f(x,y,y¢,…,y^(n-1)), (2) говорят, что ДУ (1) разрешено относительно старшей производной.

В решениях задач 1-3 присутствует постоянная интегрирования С, таком образом, эти уравнения имеют бесконечно много решений.

1.2. Дифференциальные уравнения первого порядка.

Задача Коши.

Определение. Дифференциальным уравнением первого порядка будем называть ДУ вида: y¢=f(x,y), (3) где функция f(x,y) определена на некоторой области ГÍR².

В предыдущем параграфе был сделан вывод о том, что ДУ имеет бесконечное множество решений. Для того чтобы отыскать одно из решений, необходимо задать некоторые начальные условия.

Определение. Задачей Коши будем называть следующую задачу: найти решение ДУ , такое, чтобы выполнялось условие у(х₀)=у₀.

Решение задачи Коши называют частным решением ДУ.

Решение ДУ зависит не только от переменной х, но и от некоторой постоянной С. То есть решение ДУ есть функция у=j(х,С).

Определение. Общим решением ДУ называется функция у=j(х,С), такая что выполняются два условия:

1) "С у=j(х,С) – решение ДУ;

2) "(х₀,у₀)ÎГ $!С₀ j(х₀,С₀)=у₀.

Теорема. (Существование и единственность решения задачи Коши)

Пусть функция f(х,у) непрерывна по своим переменным внутри некоторой области Г и имеет в этой области непрерывную частную производную . Тогда в этой области существует и единственно решение задачи Коши.

Замечание. Решение задачи Коши в области Г может существовать, но не быть единственным. Это возможно в случае не выполнения условий теоремы.

Пример. Найти решение задачи Коши: 1) , у(0)=3; 2) , у(0)=0.

Решение. 1) найдем общее решение ДУ .

; . Так как в обеих частях уравнения стоят дифференциалы некоторых функций, проинтегрируем обе части уравнения. ; . Найдем решение задачи Коши, соответствующее условию у(0)=3. у(0)=3tg(0)+C=3; C=3. Таким образом, решением задачи Коши является функция у(х)=3tgх+3.

Ответ: у(х)=3tgх+3.

2) Найдем общее решение ДУ . ; . Так как в обеих частях уравнения стоят дифференциалы некоторых функций, проинтегрируем обе части уравнения. ; . Найдем решение задачи Коши, соответствующее условию у(0)=0. ; С=0. Таким образом, решением задачи Коши является функция .

Ответ: .