1 Поясните следующие понятия: «функция надежности», «функция ненадежности», «интенсивность отказов элемента», математическое ожидание и дисперсия времени безотказной эксплуатации элемента».

Вероятность безотказной работы элемента в зависимости от времени t называют функцией надёжности элемента.

τ-время жизни элемента. Q(t) = P(τ<t) - вероятность отказа элемента ; P(t) = 1-Q(t) = P(τ>t)

q(t)=dQ(t)/dt –плотность вероятности отказа(частота отказов)

Статистическое определение функции надёжности:

P(t) =n(t)/N; N-количество элементов в момент времени t=0; n(t)- количество элементов в момент времени t.

λ (t) ≈Δn(t)/ (Δt*n(t)) – статистическая оценка интенсивности отказов.

λ (t) ≈Δn(t)/ (Δt*n(t)) = N* Δn(t)/( Δt*n(t)*N)= q(t)/P(t)=-P`(t)/P(t).

Функция интенсивности отказов λ (t)-есть вероятность того, что элемент, проработавший безотказно в течение времени t, откажет в течение следующего, бесконечно малого интервала времени.

T₀ =M[τ]= - среднее время жизни элемента( безотказной экспл. элемента)

D τ = M[(τ-T₀ )² ]=2 ²₀ – дисперсия времени жизни элемента( безотказной работы).

2. Приведите выражения для определения функции надежности, интенсивности частоты отказов элемента на основе статистических испытаний партии, состоящей из однородных элементов.

6. Перечислите и поясните основные свойства простейшего потока отказов Пуассона.

№3 Приведите зависимость интенсивности отказов элемента от времени и поясните особенности различных этапов его эксплуатации.

Р ис.1 - Зависимость изменения интенсивности отказов от времени

В первый отрезок времени, называемый периодом приработки, выходят из строя элементы, имеющие грубые дефекты, не вскрытые контролем.

После выявления этих элементов интенсивность отказов уменьшается и далее остаётся постоянной, наступает период нормальной работы.

По мере износа элементов интенсивность отказов вновь возрастает, начинается период старения элементов.

З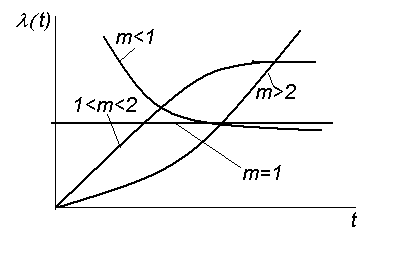 начение периода приработки при эксплуатации следует учитывать в обязательном порядке. Именно в этот отрезок времени проявляются недостатки выходного контроля качества на предприятии изготовителе, а также ошибки, допущенные при транспортировке техники. Типовое значение этого периода составляет 2-3 недели с момента ввода изделия в эксплуатацию. Отказы в период приработки подчиняются закону Вейбулла (m < 1): .

Учет периода приработки – как аппроксимация функции надежности в этот период:

, ,

- из условий и .

В период нормальной эксплуатации могут происходить внезапные отказы, которые имеют случайный характер (механические повреждения, повреждения вследствие неблагоприятных внешних условий и т.д.). Природа таких отказов обусловлена неожиданной концентрацией нагрузок внутри изделия (или извне). Закон распределения отказов в этот период экспоненциальный:

.

Период старения и износа характеризуется резким увеличением интенсивности отказов и связан с интенсивным износом и старением, необратимыми физико-химическими процессами в материалах, из которых изготовлены элементы и их части (постепенные отказы). Закон распределения отказов — либо нормальный (логарифмически-нормальный) ,

либо закон Вейбулла (m > 2), (могут быть и другие случаи).

4.При каком характере интенсивности отказов справедлив экспоненциальный закон надежности? Определите математическое ожидание и дисперсию времени безотказной эксплуатации элемент при этом законе надежности.

Экспоненциальный закон надёжности

Д ля широкого класса элементов можно принять λ(t)=const

Важным свойством экспоненциального закона надёжности является то, что вероятность отказа элемента на интервале времени (t,t+Δt) не зависит от времени предшествующей работы t, а только от ширины интервала Δt.

Экспоненциальному закону подчиняются только отказы, носящие случайный характер. Отказы, связанные с приработкой или старением элемента этому закону уже не подчиняются.