Агрегативные системы

В 1960-х годах было введено понятие класса моделей сложных систем, названных агрегативными. Основным элементом построения таких моделей был кусочно-линейный агрегат (КЛА). Эти модели обладают рядом привлекательных свойств, позволяющих использовать их в рамках общей схемы исследования сложных систем. В работах отечественной научной школы интенсивно исследовались их структурные и поведенческие свойства, создана имитационная система АИС (агрегативная имитационная система), базирующаяся на понятии агрегативной модели.

Рассмотрим определения и конструкции, приведенные ниже, в форме, приближенной к их программной реализации.

Определение кусочно-линейного агрегата (КЛА).

КЛА относится к классу объектов, которые принято изображать в виде преобразователя (рис. 4.3.1), функционирующего во времени и способного воспринимать входные сигналы х со значениями из некоторого множества X, выдавать выходные сигналы у со значениями из множества Y и находиться в каждый момент времени в некотором состоянии z из множества Z.

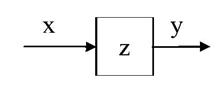
Рис.4.3.1. Общий вид преобразователя

 

Класс КЛА отличает специфика множеств X, Y, Z, допустимые формы входных и выходных сообщений (т. е. функций х (t) и у (t), ), траекторий z (t), , а также способ преобразования входного сообщения в выходное. Отметим, что динамика КЛА носит “событийный” характер.

В КЛА могут происходить события двух видов: внутренние и внешние. Внутренние заключаются в достижении траекторией КЛА некоторого подмножества состояний; внешние – в поступлении входного сигнала.

Между событиями состояние КЛА изменяется детерминированным образом. Каждому состоянию z ставится в соответствие величина, трактуемая как потенциальное время до наступления очередного внутреннего события. Состояние КЛА в момент t* – наступление события является случайным.

В момент t*, наступления внутреннего события,  выдается выходной сигнал у*, содержание которого зависит лишь от z*. В частности, выходной сигнал может быть и пустым, т. е. не выдаваться. После случайного скачка x (z) вновь определяется время до наступления внутреннего события.

Рассмотрим момент t** наступления внешнего события, связанного с поступлением входного сигнала. Тогда состояние КЛА в момент t** является случайным, зависящим лишь от х и z**. В момент t**, выдается выходной сигнал

у **, содержание которого определяется х и z**.

Условимся считать, что если моменты наступления внешнего и внутреннего событий совпадают, то изменение состояния осуществляется в соответствии с правилом наступления внешнего события, т. е. входные сигналы имеют приоритет над внутренними событиями.

Таким образом, динамику КЛА можно представить в следующем виде. Пусть в некоторый момент задано состояние КЛА. Тогда определяется время T(z), через которое совершается случайный скачок, и меняется состояние. Начиная с момента наступления события (внешнего или внутреннего), ситуация повторяется, и динамику КЛА можно описать в виде задания фазовой траектории изменения состояний z (t), определен­ной на . Процесс функционирования КЛА полностью определяется изменениями, происходящими в особые моменты времени – моменты наступления событий (внешних или внутренних). Между особыми моментами состояние КЛА меняется детерминировано.

Опишем теперь КЛА более подробно. КЛА внешне имеет вид многополюсника с m входными клеммами и n выходными клеммами (рис.4.3.2). Отметим, что в общем случае для различных КЛА .

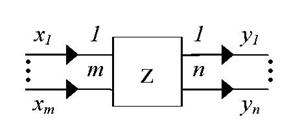
Рис.4.3.2. Кусочно-линейный агрегат

 

Предположим, что в состав множеств X_i и Y_j включены и фиктивные элементы 0, наличие которых на входе или выходе КЛА означает отсутствие сигнала на соответствующей входной или выходной клемме.

Следовательно, входной сигнал на КЛА имеет вид

а выходной:

Рассмотрим, на чем основана программная реализация агрегативных моделей. Не фиктивными входными х_i или выходными y_j сигналами, а также состояниями z КЛА являются данные. Данными считаются: элементарные данные; списки данных; массивы данных; структуры данных. Элементарными данными считаются целые числа, действительные числа, символьные переменные. Здесь термины “список”, “массив” употребляются в их обычном смысле. Понятие структуры данных соответствует дереву, на корнях которого размещены данные. Каждое данное имеет свое имя. Рассматриваемые данные хорошо отображают содержательные представления, существующие у исследователя относительно реальных объектов, и существенно облегчают процесс построения модели. Эти данные удобны как с математической, так и с программной точек зрения.

Пусть состояние z КЛА определено как некоторая структура данных. Тем самым фиксирован вид дерева, представляющего эту структуру.

Дерево базируется, в конечном счете, на элементарных данных. Обозначим через I_z элементарные данные, входящие в состояние z и имеющие тип целых чисел и символов, а через R_z , – элементарные данные, имеющие действительный тип. Предположим, что значения и состав элементарных данных могут меняться лишь в особые моменты времени, а между ними остаются постоянными. Разобьем множество R_z на два подмножества R =, где состоит из положительных величин, a – из неположительных. Будем считать, что данные из подмножества остаются неизменными между особыми моментами времени. Это отвечает обычно используемой “энергетической интерпретации” причин наступления внутренних событий в моменты, когда исчерпывается некоторый  ресурс,  заканчивается  операция  и  т.  д.  Таким  образом, внутреннее событие происходит, когда хотя бы один из положительных элементов множества обращается в нуль.

Аналогично задается реакция КЛА на входной сигнал

Введенное понятие агрегативной системы дает возможность описания самых разнообразных объектов реального мира в агрегативном виде.

Агрегативные системы служат определенным обобщением таких хорошо известных схем, как автоматы и модели массового обслуживания. Нетрудно понять, что в агрегативном виде также могут быть представлены сети Петри и практически любые численные методы решений дифференциальных уравнений (обыкновенных и в частных производных). Таким образом, агрегативные системы охватывают широкий класс различных моделей, используемых при изучении сложных систем. В агрегативном виде можно также представить модели, имеющие вид “черного ящика”. Структуры данных, описывающие состояния и сигналы агрегативных систем, помогают формализовать концептуальное представление, которое существует у пользователя относительно элементов сложной системы.

Эти описания достаточно естественны и удобны, что можно объяснить следующими причинами. Агрегативные модели соответствуют основным концепциям описания сложных систем. В основу понятия агрегативной модели положено структурное представление системы в виде взаимодействующих элементов – КЛА. Это соответствует одной из основных концепций сложных систем.

Динамика агрегативной системы полностью определяется последовательностью событий, происходящих в ней, что отвечает концепции алгоритмической модели динамической сложной системы.

В соответствии с алгоритмической моделью и понятием агрегативной системы возможны реализации разнообразных машинных моделей сложных систем. Одним из преимуществ является удобство реализации агрегативных систем на ЭВМ. Примером может являться агрегативная имитационная система.

Таким образом, можно констатировать, что агрегативная формализация удовлетворяет основным требованиям, предъявляемым к моделям сложных систем.