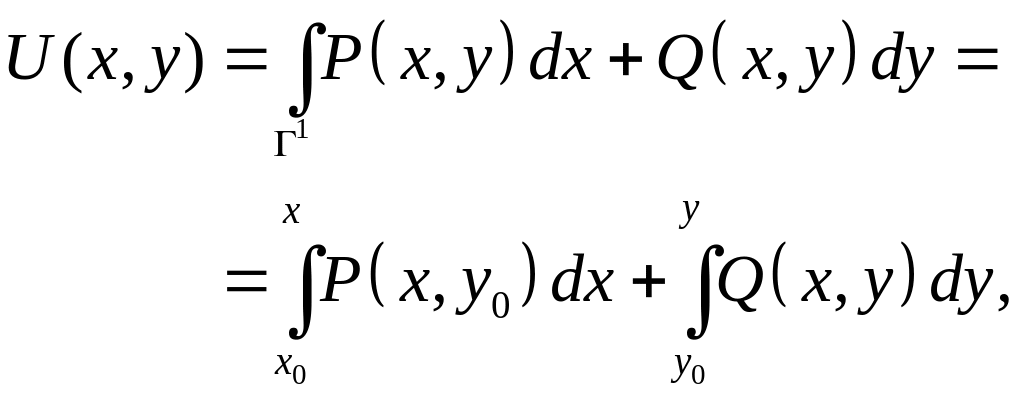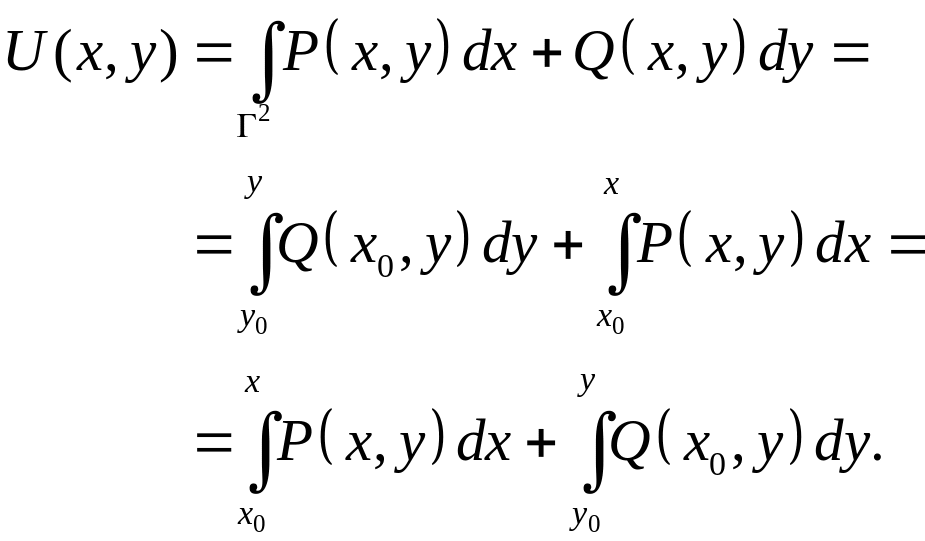§9.10. Формула Грина.

Напомним, что областью в называется открытое (состоит из внутренних точек) и связное (каждые две точки можно соединить непрерывной кривой) множество. Замкнутая область получается из области, если к области добавить её границу.

Область называется адносвязной, если для каждого простого контура область , ограниченная этим контуром, содержится в .

def. Будем говорить, что простой контур ориентирован положительно, если при обходе контура ограниченная им область остаётся слева. Противоположно ориентированный контур будем абозначать .

Теорема 1. (Формула Грина по элементарной области). Пусть область есть элементарная относительно обеих координатных осей, т.е.

где и – непрерывные и кусочно непрерывно-дифференцируемые, причём и . Если функции и непрерывны на и имеют непрерывные частные производные и , то справедлива формула Грина

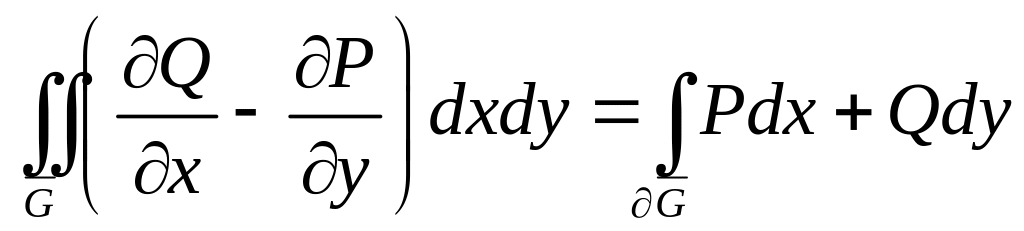, (1)

где КрИ-2 вычисляется по положительно ориентированной границе области .

Здесь – кривая , – кривая , – кривая , – кривая .

□ Пользуясь формулой приведения двойного интеграла к повторному, получим

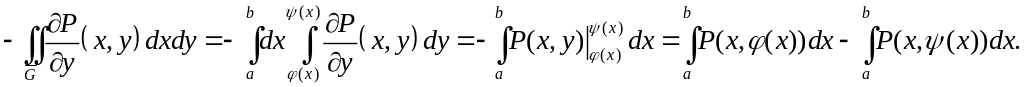Согласно формуле (6) §9.9 первый из этих определённых интегралов есть криволинейный интеграл , а второй – . Тем самым

.

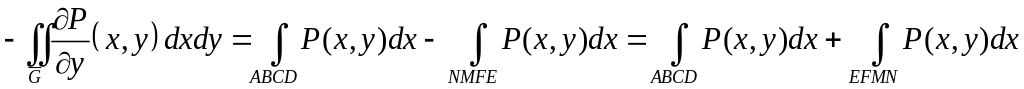Если к правой части этого равенства добавить (см. замечание 3 §9.9) и , то получим 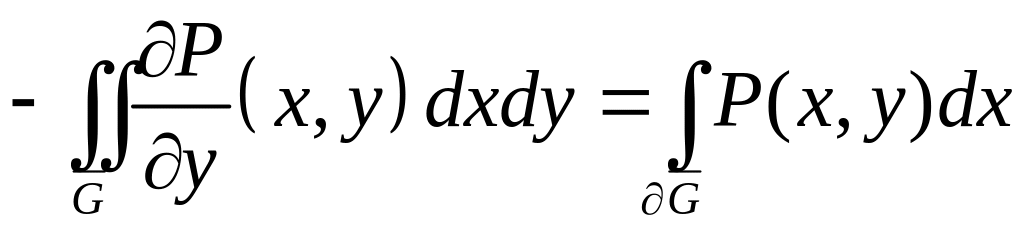. (2)

Поскольку область есть также элементарная относительно оси , то аналогично доказывается, что . (3)

Складывая равенства (2) и (3), получаем формулу Грина (1). ■

Замечание 1. Формула Грина остаётся верной и в том случае, если область неэлементарная относительно обеих координатных осей и неодносвязная, но её граница есть простой кусочно-гладкий контур.

Формула Грина даёт возможность вычислять площадь плоской фигуры при помощи КрИ-2. Действительно, если взять , то из формулы (1) получим

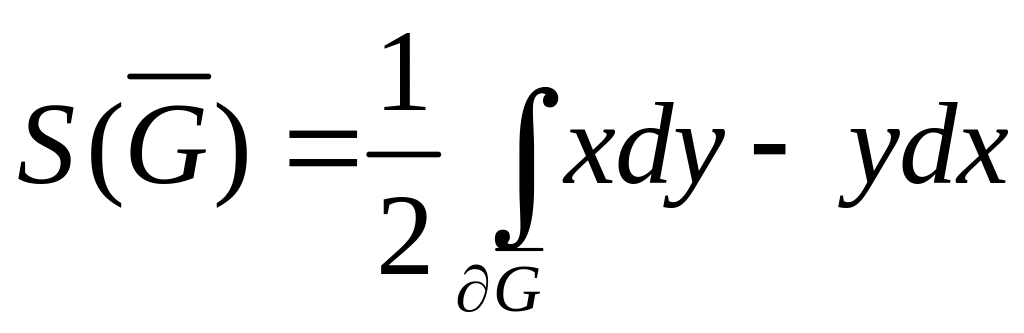, откуда . (4)

Теорема 2.(Критерий независимости КрИ-2 от кривой интегрирования.) Для того чтобы КрИ-2 от непрерывного векторного поля по кривой

(5)

не зависел от кривой , соединяющей две фиксированные точки из , необходимо и достаточно, чтобы для любого замкнутого контура выполнялось равенство . (6)

□ (Необходимость) Пусть интеграл (5) не зависит от кривой , а только от её начала и конца. Возьмём произвольный контур и зафиксируем на нём точки и . Тогда , а

= .

(Достаточность) Пусть имеет место (6). Возьмём произвольные точки и рассмотрим произвольные кривые . Пусть . Тогда

, откуда следует – КрИ-2 (5) не зависит от кривой интегрирования, соединяющей точки и . ■

def. Векторное поле называется потенциальным на области , если существует такая дифференцируемая функция , что

, (7)

т.е. . Функцию называют потенциалом векторного поля .

Теорема 3. (Критерий потенциальности непрерывного векторного поля.) Для того, чтобы непрерывное в области векторное поле было потенциальным, необходимо и достаточно, чтобы КрИ-2 из (5) не зависел от кривой , соединяющей любые две фиксированные точки из области .

□ (Необходимость) Пусть векторное поле является потенциальным и его потенциал, т.е. имею место равенства (7). Пусть кривая задаётся уравнением , причём . Согласно определению КрИ-2

Т.е. интеграл не зависит от пути интегрирования. При этом он равен разности значений протенциала поля на концах кривой интегрирования.

(Достаточность) Пусть не зависит от кривой интегрирования . Пусть – фиксированная, а – произвольная точки области , и – произвольная кусочно гладкая простая кривая, соединяющая точки и . Поскольку интеграл не зависит от кривой интегрирования, то

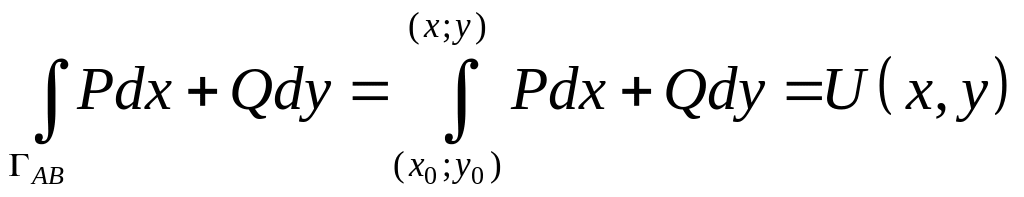– (8)

является функцией от переменной верхней границы. Покажем, что эта функция есть потенциал векторного поля .

При достаточно малом отрезок также принадлежит .

Такой выбор возможен, поскольку – открытое множество, т.е. точка входит в область вместе с окрестностью. Рассмотрим приращение функции по переменной

Таким образом,

Аналогично получается 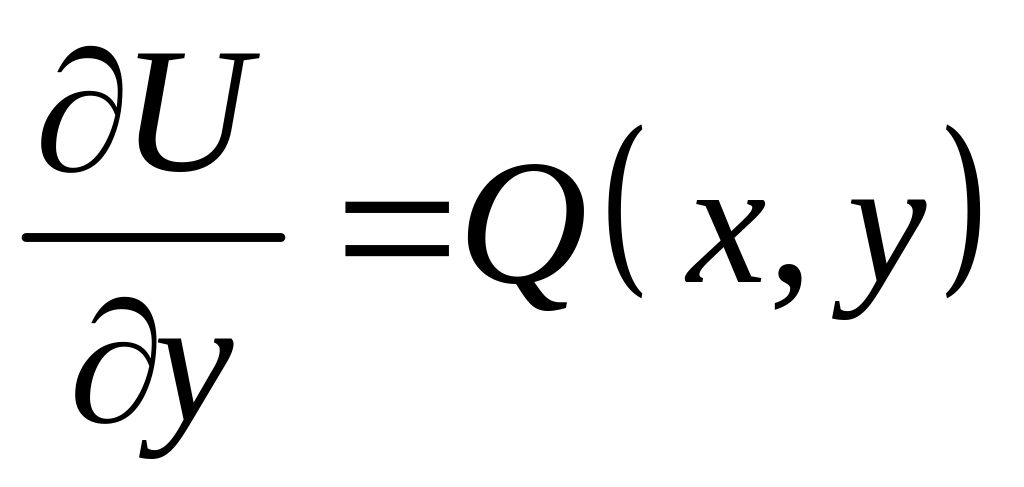, т.е. выполняются условия (7). Поскольку и непрерывные в , то – непрерывно дифференцируемая в и поэтому является потенциалом поля . ■

Следствие. Если векторное поле потенциальное в и – его потенциал, то для любой простой кривой , где и соответственно её начало и конец, имеет место .

Теорема 3 не даёт практического ответа на вопрос о потенциальности векторного поля . Для односвязной области получим критерий потенциальности, который основывается на формуле Грина.

Теорема 4. (Критерий потенциальности непрерывно дифференцируемого векторного поля) Для того чтобы непрерывно дифференцируемое в односвязной области векторное поле было потенциальным, необходимо и достаточно, чтобы в области выполнялось равенство 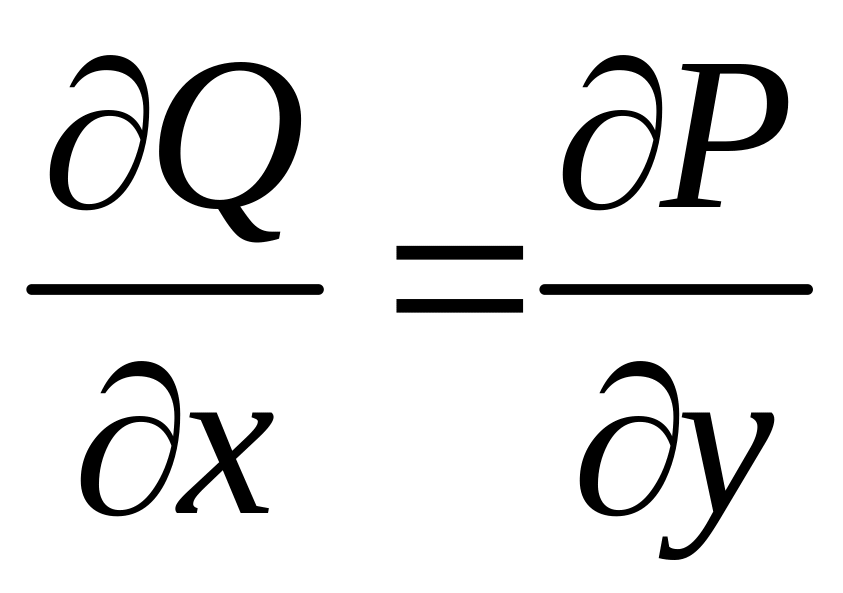. (9)

□ (Необходимость) Пусть поле есть непрерывно дифференцируемое и потенциальное, т.е. ,

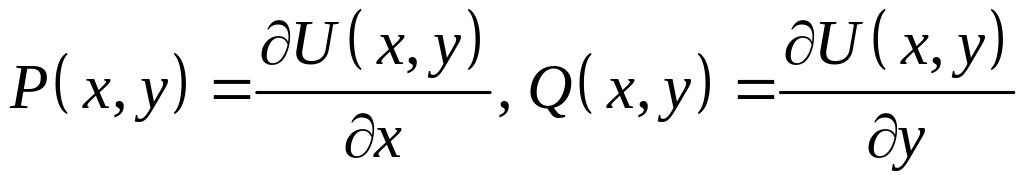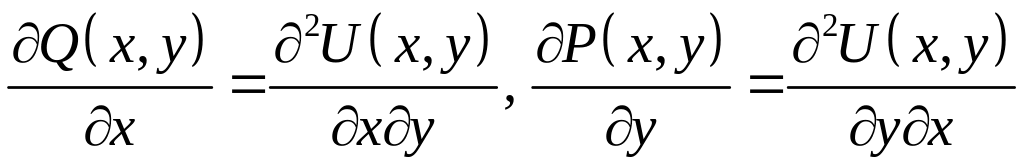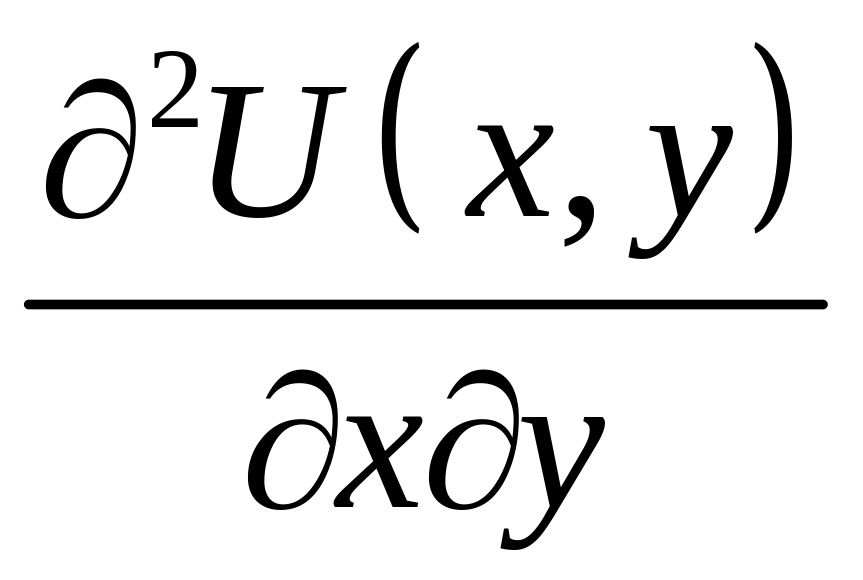откуда . Поскольку производные и непрерывные, то смешанные производные и 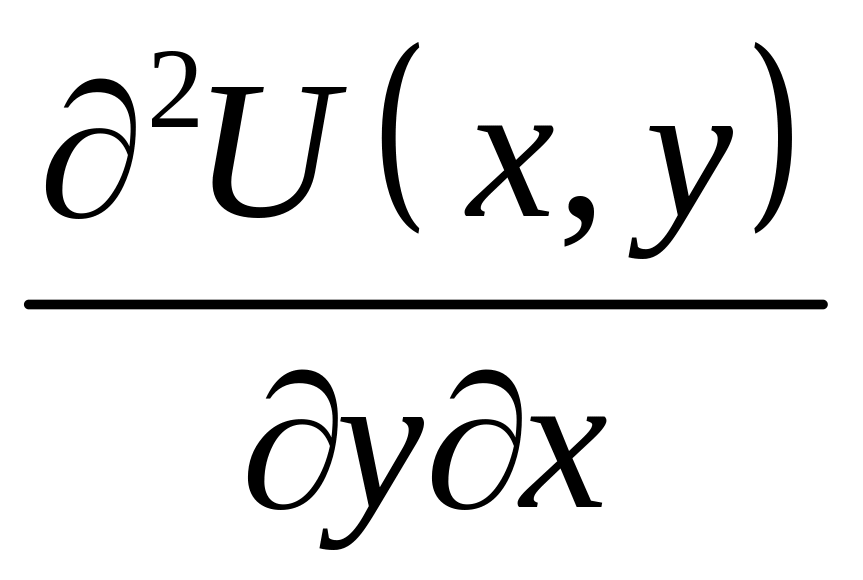также непрерывные, а, значит, равные. Условие (9) выполняется.

(Достаточность) Пусть поле задано в односвязной области и выполняется условие (9). Пусть простой контур есть граница области . Тогда на области имеет место формула Грина 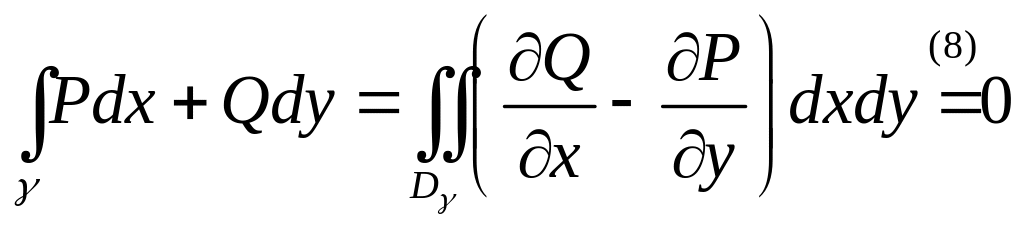. Согласно теореме 2 интеграл не зависит от кривой интегрирования, а поэтому на основании теоремы 3 поле – потенциальное. ■

Замечание 2. Если для дифференциального уравнения существует функция , то такое уравнение называют дифференциальным уравнением в полных дифференциалах. В таком случае уравнение имеет вид , а поэтому равенством неявно задаются решения уравнения. Согласно теореме 4 уравнение является дифференциальным уравнением в полных дифференциалах, если выполняется условие , причём функция находится при помощи КрИ-2

.

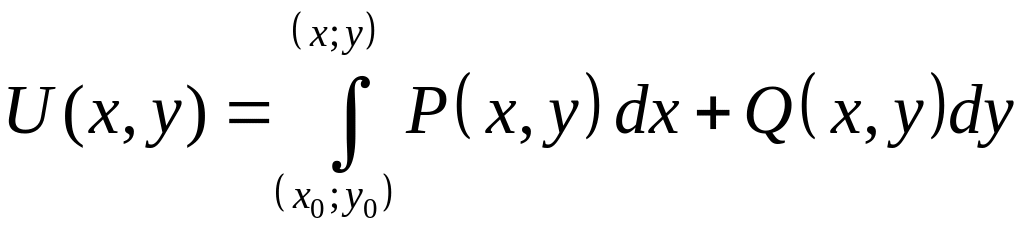Поскольку интеграл не зависит от пути интегрирования, то обычно выбирают в качестве кривой интегрирования ломаную, составленную из отрезков, параллельных осям координат:

120