2º.Сферические координаты.

(3) здесь , .

Замечание. Иногда рассматривают угол , который отсчитывается от плоскости , . Эти координаты можно называть географическими:

.

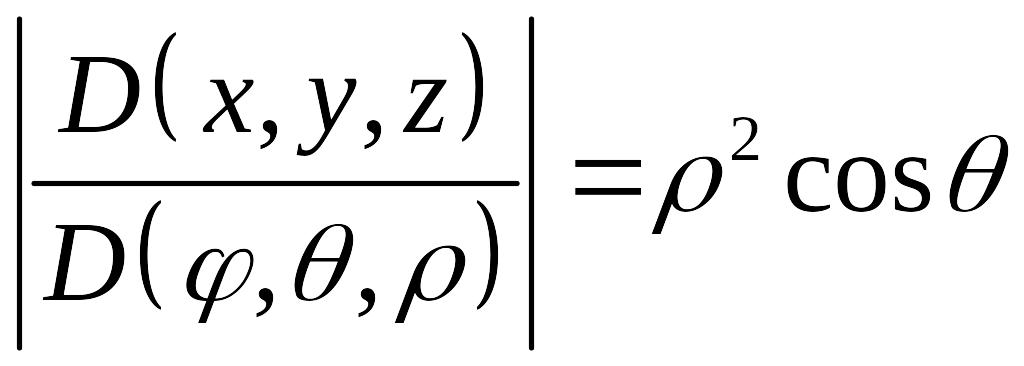Пример 4. В интеграле , где область ограничена поверхностями , перейти к сферическим координатам.

►

.

=

◄

Пример 5. Вычислить повторный интеграл , переходя к цилиндрическим и сферическим координатам.

► Сначала изобразим фигуру, по которой расставлены границы интегрирования в этом повторном интеграле

1) (цилиндрические координаты)

2) (сферические координаты)

◄

В качестве примеров использования тройного интеграла отметим следующие.

1º. Объём фигуры вычисляется по формуле .

2º. Масса фигуры с плотностью распределения массы находится по формуле .

3º.Статические моменты фигуры , плотность распределения массы которой есть , относительно координатных плоскостей соответственно равны

, ,

.

4º.Координаты центра массы фигуры с плотностью распределения массы вычисляются по формулам

§9.7. Несобственные кратные интегралы. Интеграл Пуассона.

Кратный интеграл будем называть несобственным, если область интегрирования, или подынтэгральная функция являются неограниченными.

def. Пусть – интегрируема на каждой замкнутой ограниченной области и . Несобственным интегралом от функции по области называется и обозначается . Если этот предел конечный и не зависит от выбора последовательности , то несобственный интеграл называется сходящимся.

Пример1. Исследовать на сходимость .

► Пусть . Имеем

.

Интеграл сходится, если . ◄

Пример2. Вычислить интеграл Пуассона

► Исследуем интеграл на сходимость. Сделаем замену . Имеем , , . Поскольку – ограниченная на первообразная, и функция , то, согласно признаку Дирихле, интеграл Пуассона сходится.

Далее займёмся его вычислением. Если , то , а поэтому , или . При , где – несобственный двойной интеграл. Вычислим НИ как , где .

Переходя к полярным координатам, имеем

=

Таким образом, . ◄

§9.8. Криволинейный интеграл первого рода.

Пусть в плоскости на отрезке заданы функции , . Числа и можно рассматривать как координаты

точки , или как координаты радиус-вектора .

Если переменную рассматривать как время, то уравнения

, , (1)

определяют закон движения точки . При этом множество точек , можно рассматривать как путь точки, которая движется согласно закону (1).

Отметим, что закон движения может быть очень сложным. Например, существуют такие непрерывные на отрезке функции и , что точка пробегает каждую точку некоторого квадрата.

Мы же будем рассматривать более простой случай и будем считать, что каждым двум значениям из отрезка соответствуют разные точки и . Обозначим через множество всех точек плоскости, координаты которых соответствуют уравнениям (1).

Будем говорить, что точка предшествует точке , если . Это правило упорядочивает множество . Упорядоченное таким образом множество будем называть простой кривой и записывать уравнение этой кривой в координатной форме , (2)

или в векторной форме , (3)

где . При этом переменную в уравнениях (2) и (3) будем называть параметром кривой .

Если на кривой существуют точки , то точка

называется точкой самопересечения кривой . Простая кривая не имеет точек самопересечения.

Если равенство выполняется только при , то кривую называют замкнутой или простым контуром.

Например, кривая есть простой контур. Точка является началом и концом кривой .

Кривую с началом в точке и концом в точке будем обозначать .

Уравнение определяет кривую , ориентированную противоположно кривой , задаваемой уравнением (3). Её начало совпадает с концом кривой , а конец – с началом .

def. Кривая (2) называется гладкой, если функции непрерывно дифференцируемые на отрезке , причём . Это значит, что в каждой точке кривой существует касательная, угловой коэффициент которой есть , или .

def. Пусть на некотором множестве, содержащем кривую , задана непрерывная функция . Если гладкая кривая задана уравнением (2), то определённый интеграл называют криволинейным интегралом первого рода от функции по кривой (КрИ-1) и обозначают . Таким образом, . (5)

Если абозначить , то , и поэтому

. (6)

Рассмотрим свойства криволинейного интеграла первого рода.

1°. КрИ-1 не зависит от ориентации кривой.

□ Кривая задаётся равенствами (4). В определённом интеграле (6) сделаем замену :

▲

2°. .

3°. .

4°. Если и , то

.

5°. – длина кривой .

Нетрудно убедиться в том, что если кривая задаётся как график функции , то . (7)

Если же кривая задаётся в полярных координатах , то

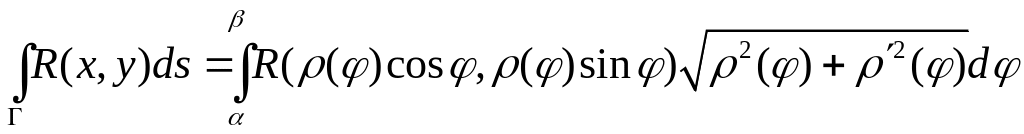. (8)

Справедливость формул (7) и (8) докажите самостоятельно.

Особенно простой вид формула (5) приобретает, если в качестве параметра взять переменную длину дуги кривой. При этом говорят, что кривая имеет натуральную параметризацию, а уравнение кривой приобретает вид , где – длина кривой . Как известно, длина дуги кривой из (3) вычисляется по формуле

.

По теореме Барроу . Если параметр , то , а поэтому равенство (5) приобретает вид . (9)

Пусть есть разбиение отрезка на частичные: . Пусть – мелкость разбиения , а . Тогда определённый интеграл из правой части равенства (9) можно записать как предел интегральной суммы

Разбиению отрезка соответствует разбиение кривой на дуги .

1) Если функция , то её можно рассматривать как линейную плотность распределения массы материальной кривой , а криволинейный интеграл можно рассматривать как массу этой кривой.

Аналогично получаем:

2) Статические моменты ;

3) Координаты центра массы .