
- •Глава 9. Кратные и криволинейные интегралы. §9.1. Двойной интеграл и его свойства.
- •§9.2. Двойной интеграл по элементарной области.
- •Пример 2. Вычислить , переходя к повторному по абоим направлениям, если ограничена кривыми : .
- •Пример 3. Вычислить повторный интеграл .
- •§9.3.Преобразование плоских областей.
- •§9.4. Замена переменных в двойном интеграле.
- •Пример 2. Вычислить площадь фигуры, ограниченной кривыми:
- •§9.5. Приложения двойного интеграла.
- •2º. Объём цилиндроида.
- •3º. Масса плоской пластинки.
- •4º. Статические моменты.
- •5º. Координаты центра массы плоской пластинки.
- •§9.6. Тройной интеграл.
- •1º. Цилиндрические координаты.
- •2º.Сферические координаты.
- •§9.7. Несобственные кратные интегралы. Интеграл Пуассона.
- •§9.8. Криволинейный интеграл первого рода.
- •§9.9. Криволинейный интеграл второго рода.
- •§9.10. Формула Грина.
4º. Статические моменты.
def. Статическим моментом точки относительно прямой называется произведение массы этой точки на расстояние до прямой.
Пусть
– плотность
распределения
массы
плоской
пластинки
,
а
– некоторое
её
разбиение. На каждой
её части
выберем
произвольную
точку
.
Если
![]() – масса
этой
точки,
то статический
момент
точки
– масса
этой
точки,
то статический
момент
точки
![]() относительно оси
равен
относительно оси
равен
![]() .
Будем считать
пластинку
однородной
и её массу
сосредоточенной
в
точке
,
а её статический
момент
.
Будем считать
пластинку
однородной
и её массу
сосредоточенной
в
точке
,
а её статический
момент
![]() .
Тогда
.
Тогда
![]() ,
а
поэтому
,
а
поэтому
 .
.
Если
,
то
 .
Аналогично
.
Аналогично
 .
.
5º. Координаты центра массы плоской пластинки.
Из
механики
известно,
что
![]() .
Поэтому
.
Поэтому

§9.6. Тройной интеграл.
Будем рассматривать
замкнутую
ограниченную
область
![]() ,
на которой
определена
непрерывная функция
,
на которой
определена
непрерывная функция
![]() .
Сделаем
разбиение области
.
Сделаем
разбиение области
![]() так, что
так, что
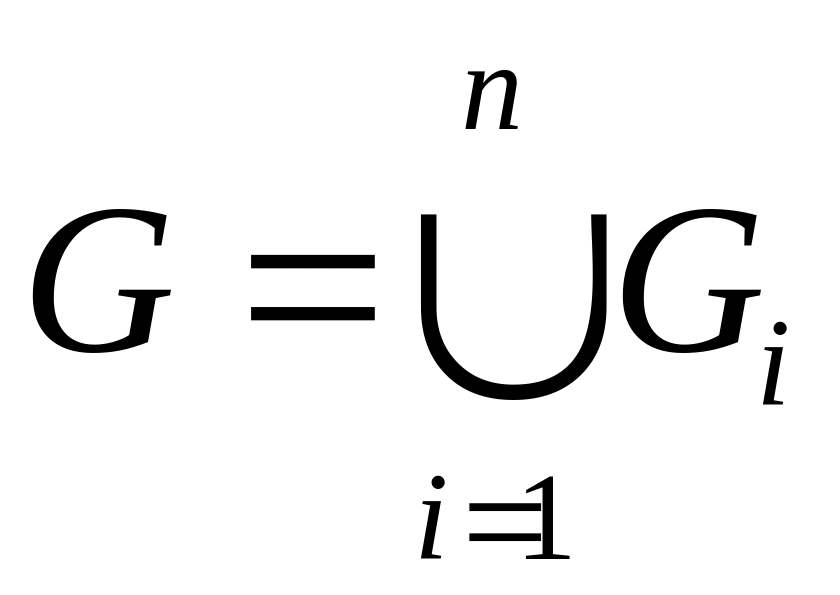 и все
и все
![]() не имеют
общих
внутренних точек. Объём
области
будем обозначать
не имеют
общих
внутренних точек. Объём
области
будем обозначать
![]() .
Под
диаметром
области
будем понимать
наибольшее
из
расстояний
между граничными
точками области,
под
мелкостью
разбиения
.
Под
диаметром
области
будем понимать
наибольшее
из
расстояний
между граничными
точками области,
под
мелкостью
разбиения
![]() будем понимать
наибольший
из
диаметров
областей
будем понимать
наибольший
из
диаметров
областей
![]() .
.
Выберем
в
каждой
области
произвольную
точку
![]() и составим
интегральную сумму
и составим
интегральную сумму
 .
Если число
.
Если число
![]() и этот
предел не зависит
ни от
разбиениея
и этот
предел не зависит
ни от
разбиениея
![]() ,
ни от
выборки
точек
,
ни от
выборки
точек
![]() ,
то число
,
то число
![]() называют тройным
интегралом
от
функции
по
области
и обозначают
называют тройным
интегралом
от
функции
по
области
и обозначают
![]() ,
или
,
или
![]() ,
,
а функцию при этом называют инегрируемой на .
Для тройного интеграла имеют место такие же свойства существования, что и для двойного интеграла.
Область
будем называть элементарной
относительно оси
Вычисление тройного интеграла проводится на основании следующей теоремы. |
|
Теорема
(тройной интеграл по элементарной
области). Пусть функция
интегрируема на области
,
элементарной относительно оси
.
Если для каждой фиксированной точки
![]() (проекция цилиндроида
на плоскость
(проекция цилиндроида
на плоскость
![]() )
существует
)
существует
 ,
то существует
,
то существует
 и он равен тройному интегралу
и он равен тройному интегралу
 .
.
В частности, если при этом область есть элементарная относительно оси , то
|
|
Пример 1.
Свести
тройной интеграл
|
|
►
Спроектируем
на плоскасць

Имеем
 .
.
Если же
область
рассматривать
как элементарную
относительно оси
,
то её
проекция
на плоскость
Поэтому
|
|
◄
Замена переменных
 (1)
(1)
в тройном интеграле осуществляется по формуле
 ,
,
где – образ области при отображении (1), а якобиан
 .
.
Рассмотрим две наиболее встречающиеся системы криволинейных координат.
1º. Цилиндрические координаты.
|
|
Координатные
поверхности:
а)
![]() – полуплоскость;
– полуплоскость;
б)
![]() – цилиндрическая
поверхность;
в)
– цилиндрическая
поверхность;
в)
![]() – плоскость.
– плоскость.

Пример 2.
В
интеграле
,
где
– цилиндр, ограниченный поверхностями
![]() ,
перейти к цилиндрическим координатам.
,
перейти к цилиндрическим координатам.
►
|
= |
◄
Пример 3. В интеграле , где область ограничена паверхностями , перйти к цилиндрическим координатам.
►
|
= |
◄




 .
.
 (2)
(2)
 .
. .
.