
- •Глава 9. Кратные и криволинейные интегралы. §9.1. Двойной интеграл и его свойства.
- •§9.2. Двойной интеграл по элементарной области.
- •Пример 2. Вычислить , переходя к повторному по абоим направлениям, если ограничена кривыми : .
- •Пример 3. Вычислить повторный интеграл .
- •§9.3.Преобразование плоских областей.
- •§9.4. Замена переменных в двойном интеграле.
- •Пример 2. Вычислить площадь фигуры, ограниченной кривыми:
- •§9.5. Приложения двойного интеграла.
- •2º. Объём цилиндроида.
- •3º. Масса плоской пластинки.
- •4º. Статические моменты.
- •5º. Координаты центра массы плоской пластинки.
- •§9.6. Тройной интеграл.
- •1º. Цилиндрические координаты.
- •2º.Сферические координаты.
- •§9.7. Несобственные кратные интегралы. Интеграл Пуассона.
- •§9.8. Криволинейный интеграл первого рода.
- •§9.9. Криволинейный интеграл второго рода.
- •§9.10. Формула Грина.
§9.4. Замена переменных в двойном интеграле.
Пусть функция
![]() непрерывна на ограниченной
замкнутой
области
.
Пусть область
отображается
взаимно
однозначно
на область
плоскости
при помощи
преобразования
непрерывна на ограниченной
замкнутой
области
.
Пусть область
отображается
взаимно
однозначно
на область
плоскости
при помощи
преобразования
 (1)
(1)
причём
обратное
отображение
области
на область
осуществляется
преобразованием
 (2)
(2)
где
![]() и
и
![]() – непрерывные
функции
вместе
с
их частными
производными
на
.
– непрерывные
функции
вместе
с
их частными
производными
на
.
Рассмотрим
задачу о преобразовании
интеграла
![]() в интеграл от
новых переменных
в интеграл от
новых переменных
![]() в соответствии с формулами
(2).
в соответствии с формулами
(2).
|
|
Разобъём
область
координатными
линиями
![]() на прямоугольники
на прямоугольники
![]() с
площадями
с
площадями
![]() .
Тогда координатные
линии
.
Тогда координатные
линии
![]()
![]() разобъют
область
на криволинейные
четырёхугольники
разобъют
область
на криволинейные
четырёхугольники
![]() с
площадями
с
площадями
![]() .
При этом
точке
.
При этом
точке
![]() соответствует
точка
соответствует
точка
![]() .
Поскольку
.
Поскольку
 ,
(3)
,
(3)
то при
мелкости
разбиения
![]() ,
стремящейся
к нулю,
мелкость разбиения
,
стремящейся
к нулю,
мелкость разбиения
![]() области
также стремится к нулю.
Таким образом,
области
также стремится к нулю.
Таким образом,
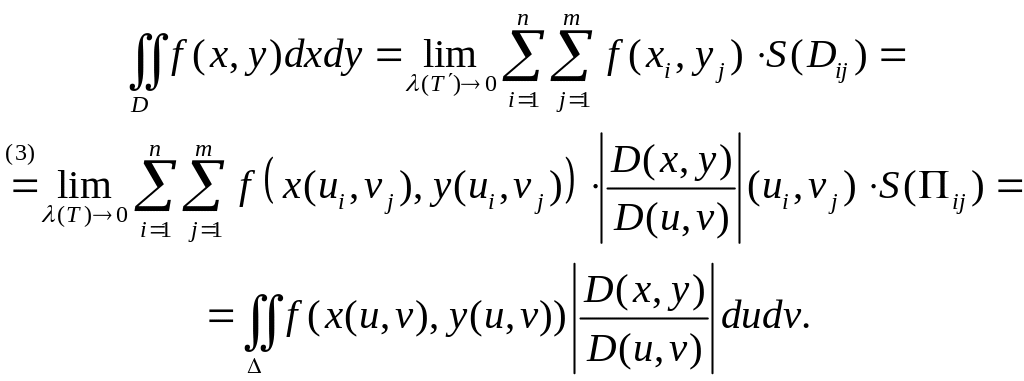 (4)
(4)
Если, в
частности,
обратиться
к полярным
координатам
![]() ,
то
,
то
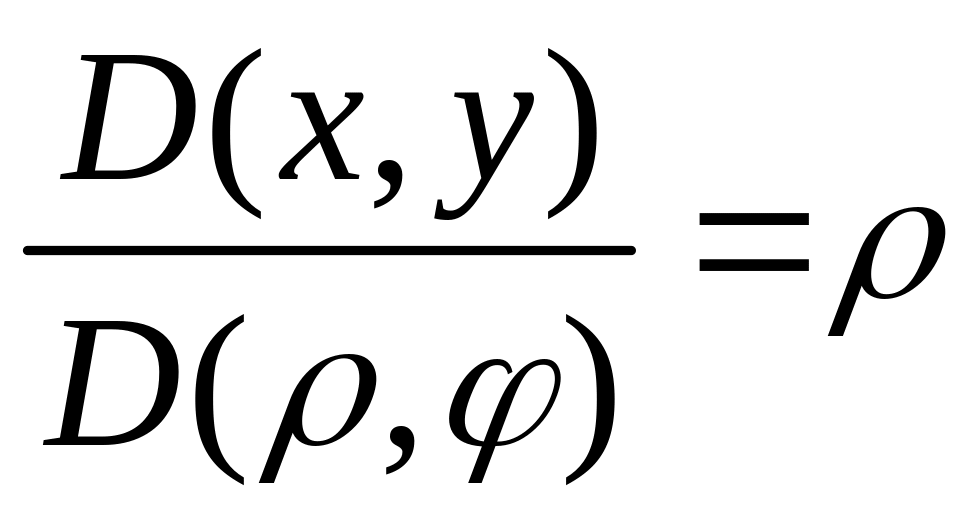 ,
,
![]() .
(4)
.
(4)
Рассмотрим два частных случая области .
а) Пусть
область
в
плоскости
ограничена
лучами
![]() и двумя
кривыми
и двумя
кривыми
![]() .
.
|
Тогда область в плоскости
относительно
оси
|
|
Имеем
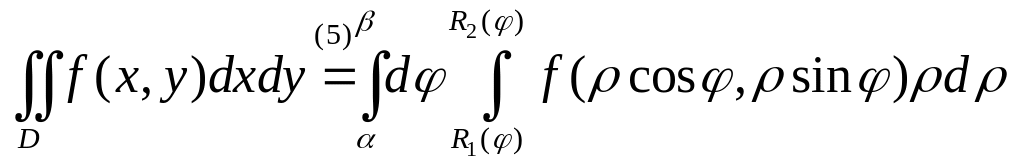 .
.
б) Если
же
область
ограничена
дугами двух
концентрических
окружностей
![]() и кривыми
и кривыми
![]() ,
то
,
то
|
|
 .
.
Пример 1.
В двойнойм
 перейти к повторному в абоих
напрвлениях
как в декартовых, так и
в полярных координатах,
где
:
перейти к повторному в абоих
напрвлениях
как в декартовых, так и
в полярных координатах,
где
:
![]()
►
 ◄
◄
Пример 2. Вычислить площадь фигуры, ограниченной кривыми:
![]()
► Фигура , ограниченная этими кривыми, имеет вид,
|
|
а поэтому
для нахождения
площади
её
придётся
разделить
на 3 части и вычислять
площадь как сумму
площадей
трёх
областей.
Но
мы
сделаем
это
иначе,
и введём
следующие
криволинейные
координаты:
![]() .
При этом
имеем
.
При этом
имеем
то фигура отображается в прямоугольник : |
|
Вычислим
якобиан
 и получим
и получим

◄
§9.5. Приложения двойного интеграла.
1º.
Площадь
плоской
фигуры.
 .
.
2º. Объём цилиндроида.
|
|
3º. Масса плоской пластинки.
Пусть
|
|
Тогда
 .
Если
,
то
.
Если
,
то
 .
.








 .
Поскольку
.
Поскольку



 Если
Если
 .
.