Глава 9. Кратные и криволинейные интегралы. §9.1. Двойной интеграл и его свойства.

Пусть – некоторая замкнутая ограниченная область, а – функция, определённая и ограниченная в . Будем считать, что граница области состоит из конечного числа кривых, заданных уравнениями вида или , где и – непрерывные функции.

Совокупность областей , которые не имеют общих внутренних точек, и таких, что , будем называть разбиением области и обозначать . Площади областей будем обозначать . Диаметром будем называть найбольшее расстояние между граничными точками этой области, т.е. . Число будем называть мелкостью разбиения .

На каждой области выберем произвольную точку и составим сумму

, которую будем называть интегральной суммой для функции на области , соответствующей разбиению и выборке = .

def. Число называется пределом интегральной суммы при мелкости разбиения , если выполняется неравенство . При этом пишут . Если число не зависит ни от разбиения , ни от выборки , то его называют двойным интегралом от функции по области и обозначают , а функцию называют интегрируемой на области .

Замечание. Давая определение двойного интеграла, мы допускаем, что функция является ограниченной. Можно было это условие не оговаривать, а доказать его как необходимое условие интегрируемости. В то же время это условие недостаточно для интегрируемости.

Например, на квадрате функция

ограничена, но неинтегрируема, что следует непосредственно из определения двойного интеграла.

Пусть , тогда – нижняя и верхняя суммы Дарбу.

Критерий интегрируемости. Для того чтобы функция была интегрируемой на , необходимо и достаточно, чтобы (тем самым эти пределы равны ).

На основании этого критерия можно доказать следующие две теоремы, которые определяют класс интегрируемых функций.

Теорема 1. Функция , непрерывная на замкнутой ограниченной области , является интегрируемой на этой области.

Теорема 2. Функция , ограниченная на замкнутой ограниченной области и непрерывная на ней везде , кроме точек, расположенных на конечном числе кривых, каждая из которых есть график непрерывной функции или , является интегрируемой на этой области.

Основные свойства двойного интеграла аналогичны соответствующим свойствам определённого интеграла.

1º. Если интегрируема на и – произвольное действительное число, то функция также интегрируема на и .

2º. Если и интегрируемы на , то их сумма также интегрируема на и .

3º. Если интегрируема на и на , то .

4º. Если и интегрируемы на и , то

.

5º. Если интегрируема на и , то она интегрируема на . Если при этом и не имеют общих внутренних точек, то

.

6º. Теорема о среднем значении. Если функция интегрируема на замкнутой ограниченной области , то существует число , причём . Если при этом непрерывная, то существует точка

.

§9.2. Двойной интеграл по элементарной области.

Теорема 1.(двойной интеграл по прямоугольнику) Пусть функция интегрируема на прямоугольнике и для каждого существует . Тогда существует повторный интеграл

и имеет место равенство . (1)

□ Рассмотрим произвольное разбиение отрезков и точками

.

Пусть , .

Если ,то .

Интегрируя эти неравенства по в границах от до , получим

.

Выбираем и придаём переменной значения . Просуммировав полученные неравенства по , получим

,

т.е. .

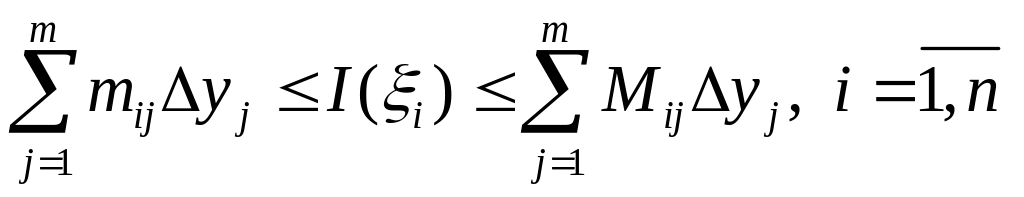Домножив эти неравенства на и просуммировав их по , получим:

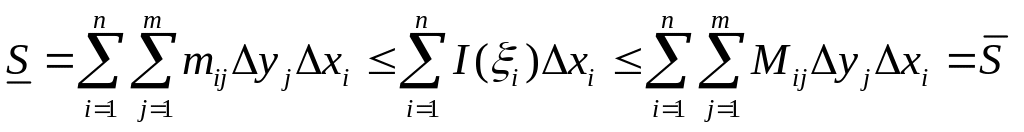. (2)

Здесь и – нижняя и верхняя суммы Дарбу, которые, в силу интегрируемости функции , удовлетворяют условию . Переходя в (2) к пределу при (при этом ), имеем

,

т.е. . ■

Замечание. Если в условиях теоремы поменять ролями и , то можно паказать, что .

Следствие. Если непрерывна на , то имеет место равенство

.

def. Пусть и – непрерывные на функции, причём . Область называют элементарной относительно оси

Теорема 2 (двойной интеграл по элементарной области). Пусть функция является интегрируемой на элементарной относительно оси области , и для каждого существует . Тогда существует повторный интеграл и имеет место равенство

. (3)

□ Пусть . Рассмотрим функцию

Поскольку – интегрируема на (как ) и на (как нуль), то по свойству двойного интеграла – интегрируема на прямоугольнике , причём . (4)

Аналогично из существования каждого из интегралов

следует, что существует . (5)

Таким образом, для функции на прямоугольнике выполняются условия теоремы 1, т.е. . Подставляя сюда выражения из (4) и (5), получаем (3). ■

Вопрос: какой геаметрический смысл интеграла ?

Пример 1. Вычислить , где .

►Поскольку круг ограничен полуокружностями , то

◄

def. Будем называть область элементарной относительно оси , если , где и – непрерывны на .

Замечание. Если функция интегрируема на области , элементарной относительно оси , то имеет место равенство .

Если же область есть элементарная относительно обеих координатных осей, то для интегрируемой на функции имеет место равенство

.