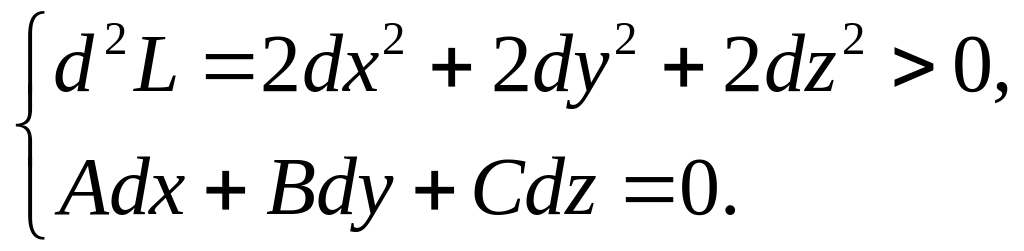Пример 2. Пусть задана точка . Найдём расстояние от до плоскости (12)
► Возьмём
произвольную
точку
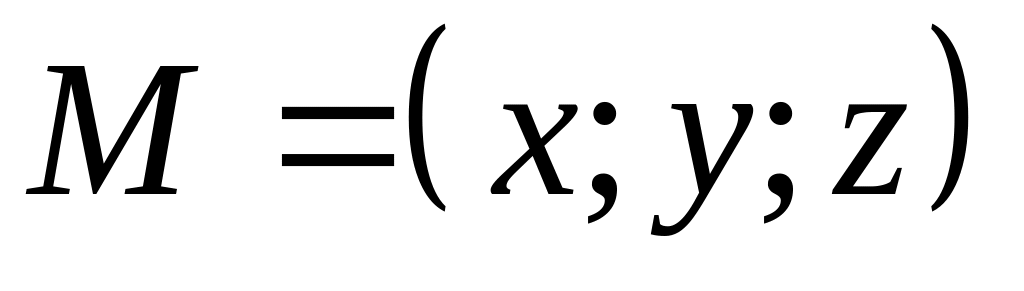 на плоскости
(12). Тогда
на плоскости
(12). Тогда
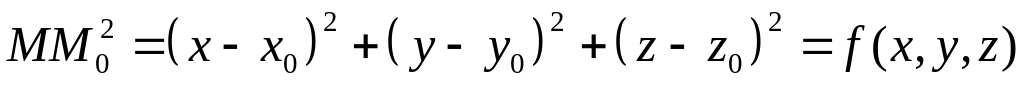 .
Искомое
расстояние
.
Искомое
расстояние
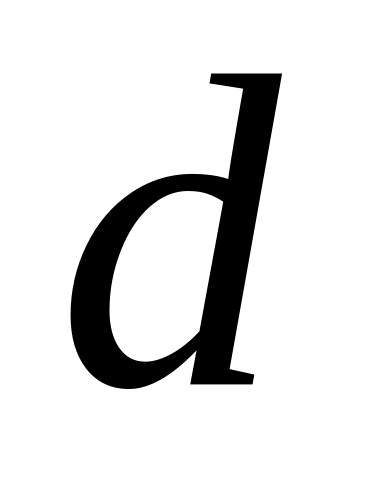 равно
минимуму функции
равно
минимуму функции
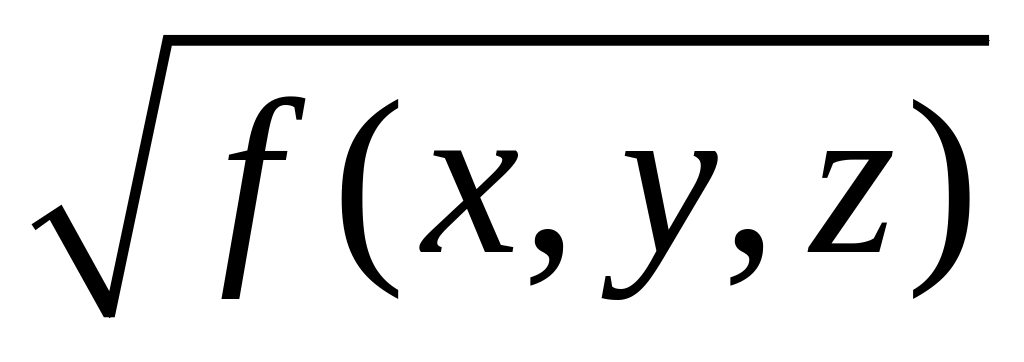 ,
который
будет
находиться
в точке
минимума
функции
.
Ищем далее минимум функции .
Рассмотрим
функцию Лагранжа
,
который
будет
находиться
в точке
минимума
функции
.
Ищем далее минимум функции .
Рассмотрим
функцию Лагранжа
и запишем
для неё
необходимые
условия
экстремума:
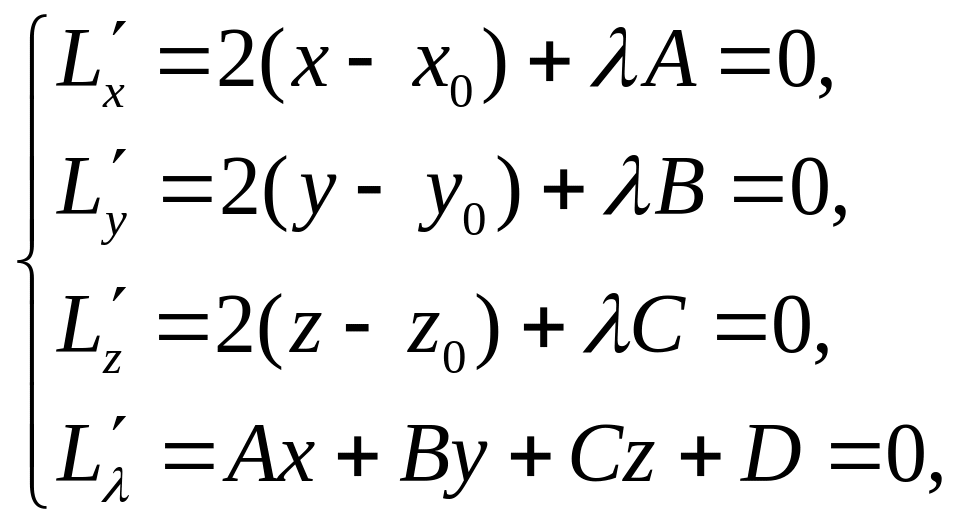
откуда
получаем
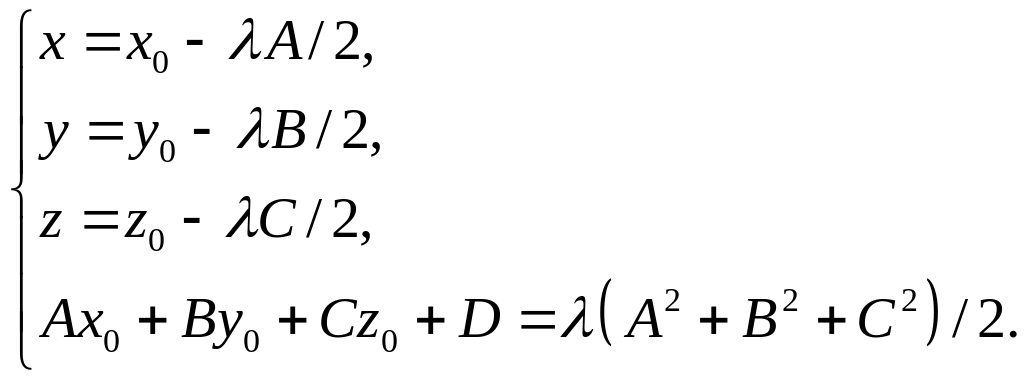 Таким образом, имеем
Таким образом, имеем
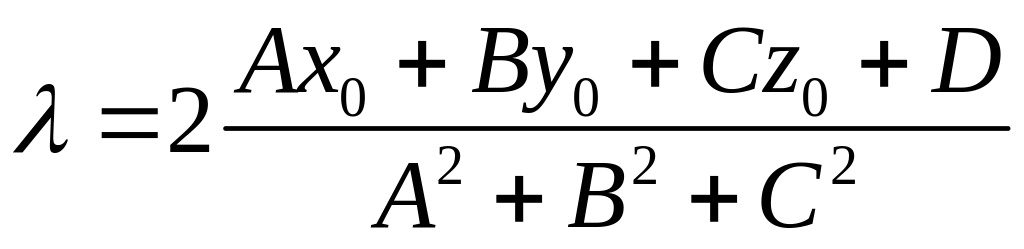 , а расстояние
будет
равно
, а расстояние
будет
равно

(поскольку здесь
единственная
точка экстремума).
То же
самое
получаем
на основании
достаточного
условия:
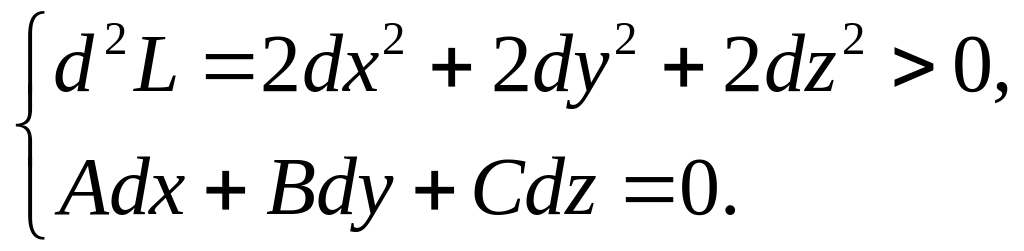
Второй
дифференциал
функции Лагранжа
есть
положительно
определённая
квадратичная
форма, а поэтому
–
искомое расстояние.
◄
77


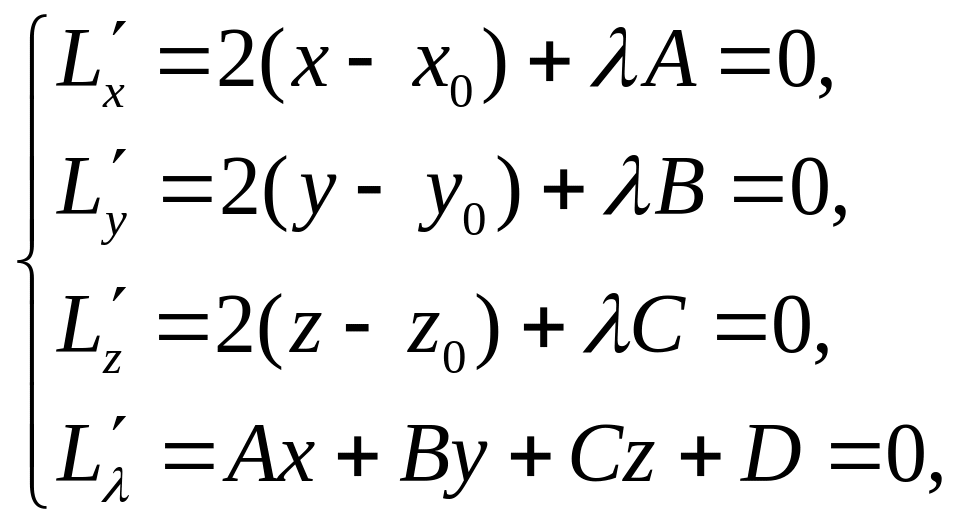
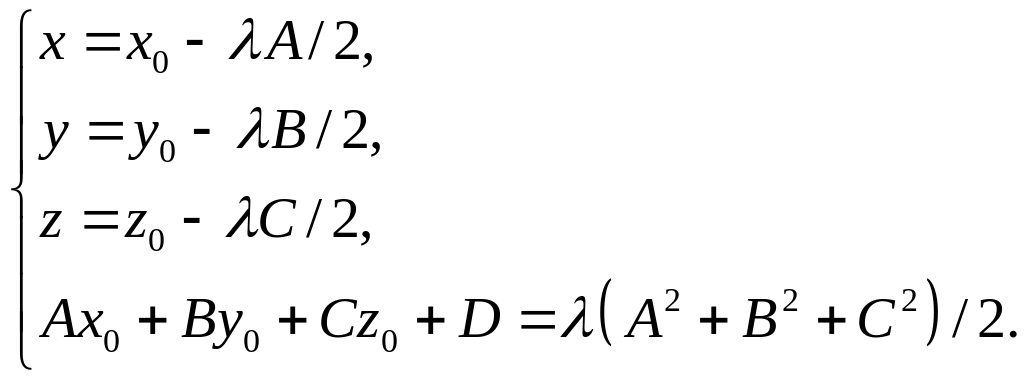 Таким образом, имеем
Таким образом, имеем