Пример 2. Пользуясь теоремой 3, исследуем на зависимость систему функций .

► Матрица Якоби имеет вид .

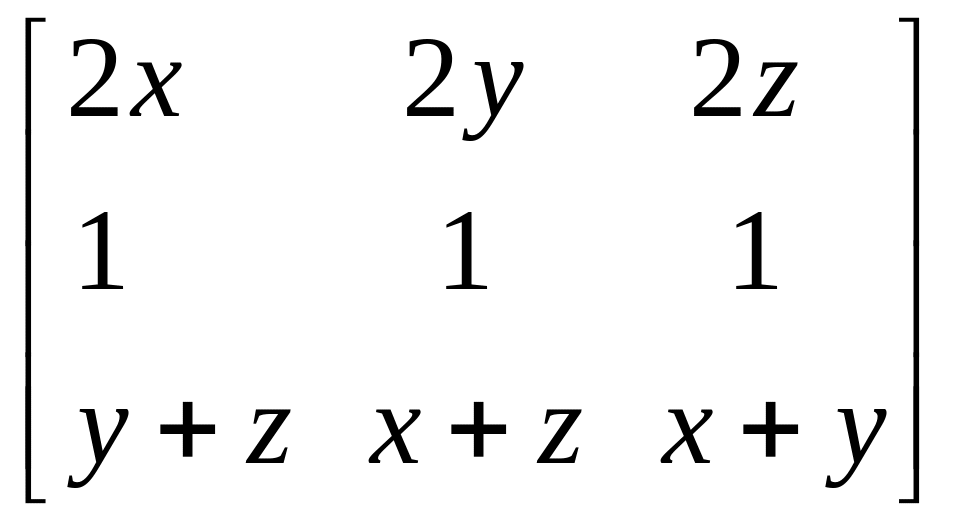Если к последней строке прибавить первую, умноженную на 1/2, то получим

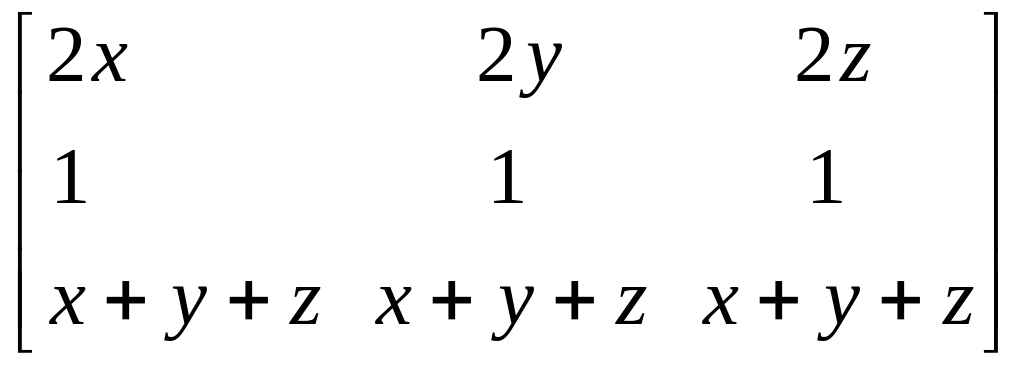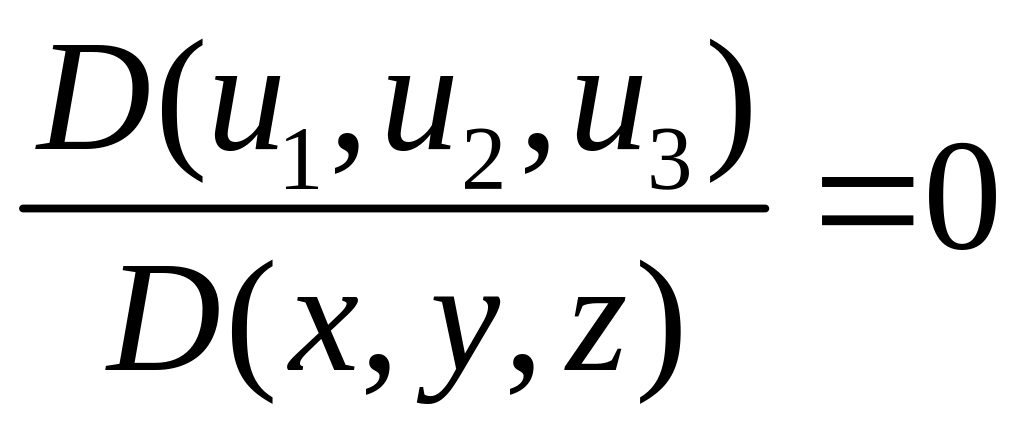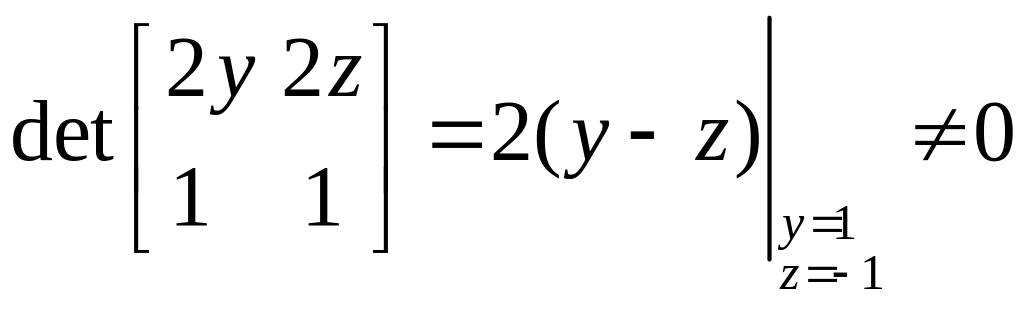, а тем самым . Поскольку , то – независимы, а . ◄

§8.4. Условный экстремум.

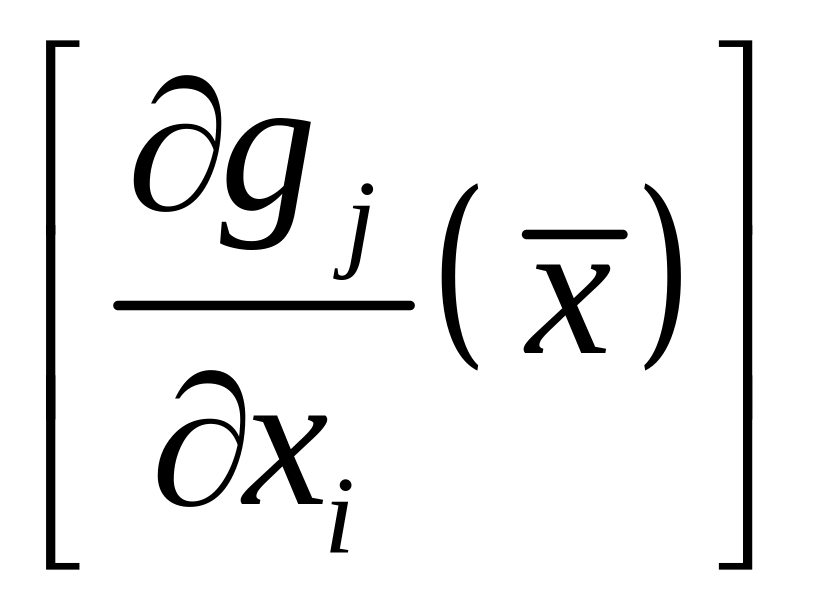Пусть функции – являются непрерывно дифференцируемыми на открытом множестве и ранг матрицы Якоби равен .

Обозначим через – множество точек , удовлетворяющих системе уравнений . (1)

Уравнения (1) будем называть уравнениями связей или просто связями.

def. Пусть на определена функция . Точка называется точкой условного максимума (минимума) функции при наличии связей (1), если

.

Если функция имеет в точке условный максимум или условный минимум, то говорят, что она имеет в точке условный экстремум.

Получим необходимые условия существования условного экстремума.

Пусть есть точка условного экстремума функции при наличии связей (1). Поскольку ранг матрицы Якоби 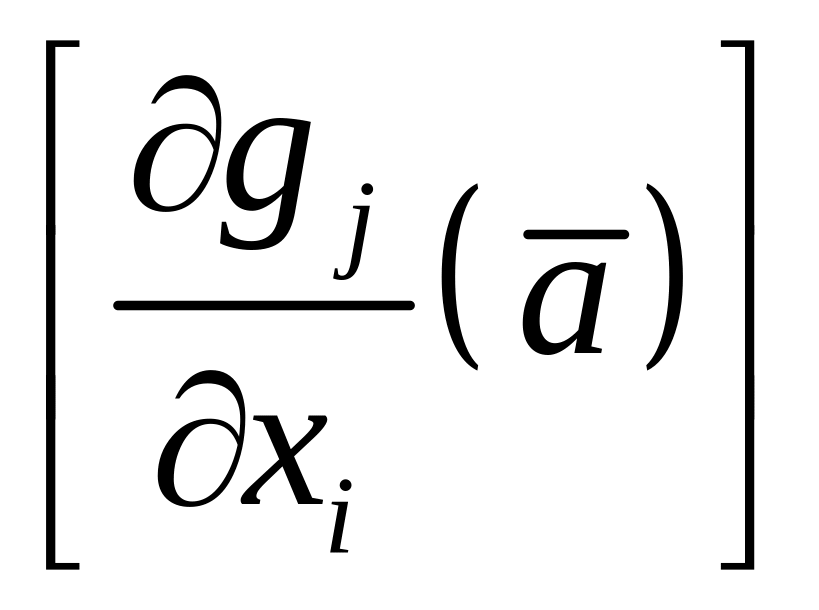равен , то, не нарушая общности дальнейших рассуждений, можно считать, что

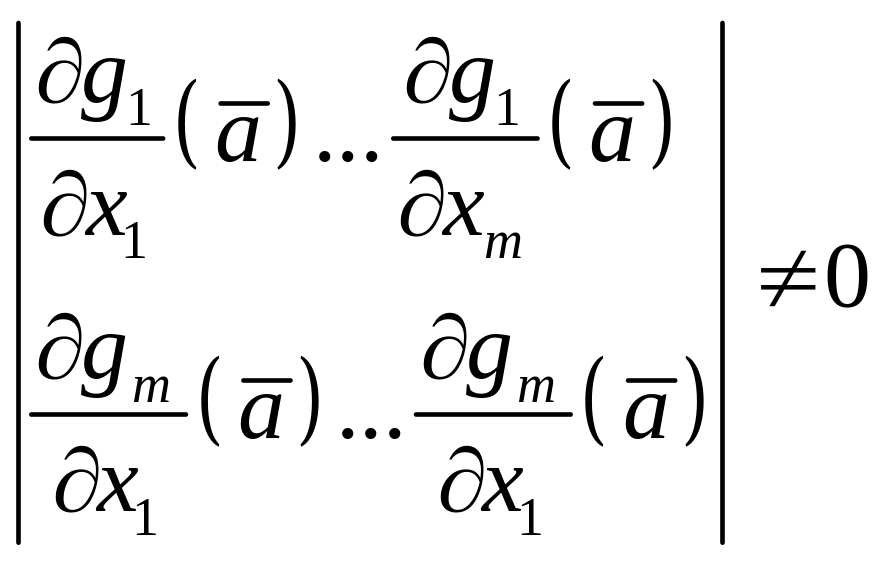. (2)

Согласно общей теореме о существовании системы неявных функций (теорема 3 § 8.2) система (1) разрешима и имеет единственное решение . При этом функции являются непрерывно дифференцируемыми и имеют место тождества

. (3)

Если рассмотреть функцию , (4)

то она является непрерывно дифференцируемой и имеет в точке локальный экстремум. Поэтому для функции в этой точке выполняются необходимые условия экстремума 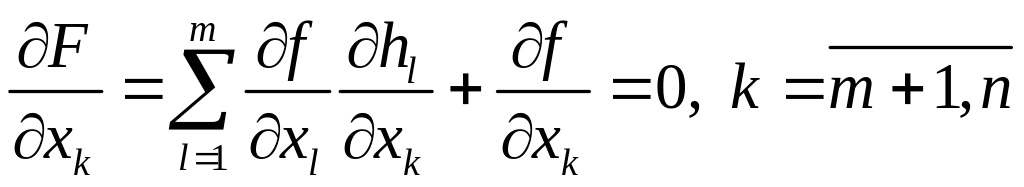. (5)

Дифференцируя тождества (3), имеем 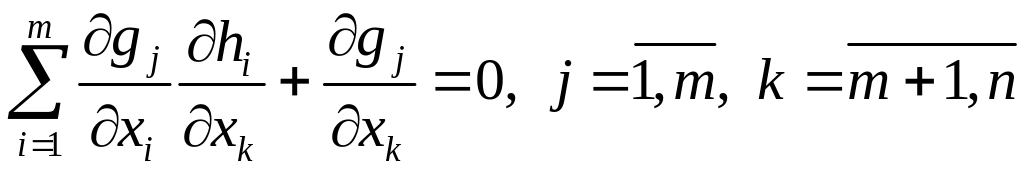. (6)

Таким образом, нами получена

Теорема 1. (необходимое условие условного экстремума). Если функция является непрерывно дифференцируемой на множестве и имеет в точке экстремум при условиях (1), то в точке выполняются условия (6), (5) и (1).

Отметим, что при этом могут возникнуть трудности с разрешением системы (1). Но, если решения системы (1) получены, то для нахождения условного экстрэмума достаточно найти локальный экстремум функции из (4).

Пример 1 Найти экстремум функции при условии .

► Для решения задачи подставим значение из условия связи в уравнение функции. Приходим к задаче нахождения экстремума функции .

Поскольку , то точка – точка минимума функции , а точка (здесь ) – точка условного экстремума функции , хотя локальный экстремум функция имеет в точке . ◄

Теорема 2. (метод множителей Лагранжа). Для таго, чтобы точка была точкой условного экстремума функции при наличии связей (1), необходимо, чтобы выполнялись условия: 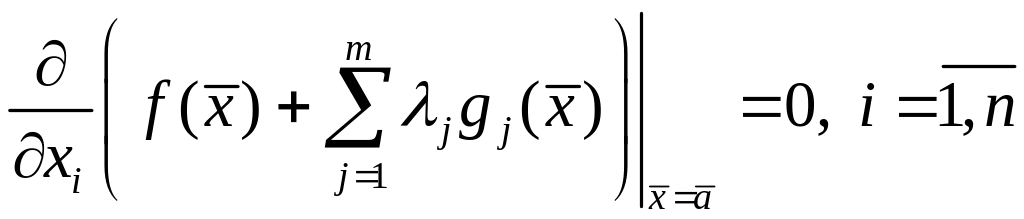, (7)

, (8)

где – некоторые константы, которые называются множителями Лагранжа.

□ Необходимость условий (8) вытекает из того, что точка условного экстремума по определению должна удовлетворять системе (1).

Рассмотрим матрицу Якоби в точке для системы функций :

. (9)

Выполнение необходимых условий (5) и (6) из теоремы (1) означает, что каждый из последних столбцов этой матрицы есть линейная комбинация первых столбцов, которые являются линейно независимыми, поскольку ранг их матрицы равен , что следует из (2). Таким образом, ранг матрыцы (9) равен также , а поэтому первая строка матрицы (9) есть линейная комбинация последних строк, которые опять таки независимы на основании (2). Это означает, что существуют постоянные :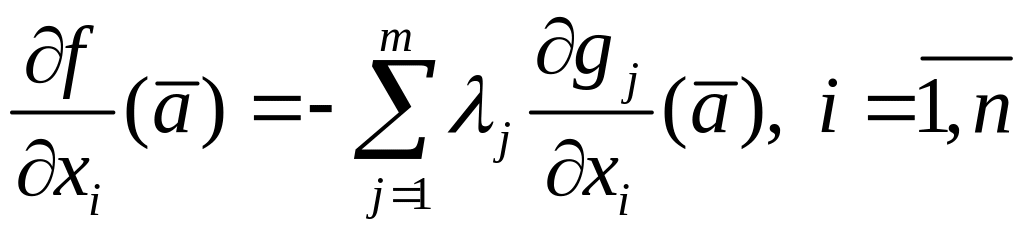 , что приводит к равенствам (7). ■

Если ввести функцию 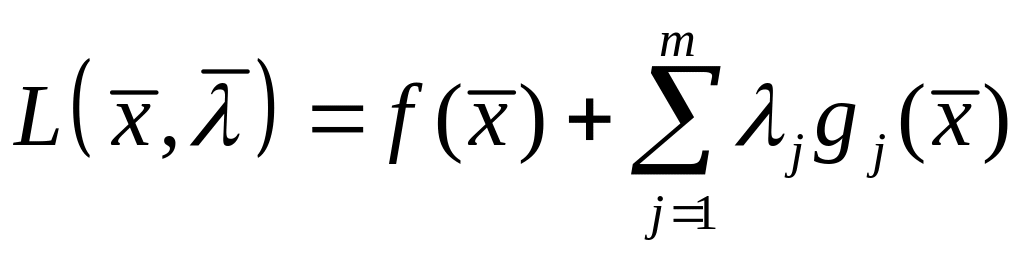, которая называется функцией Лагранжа, то условия (7) можно записать в виде 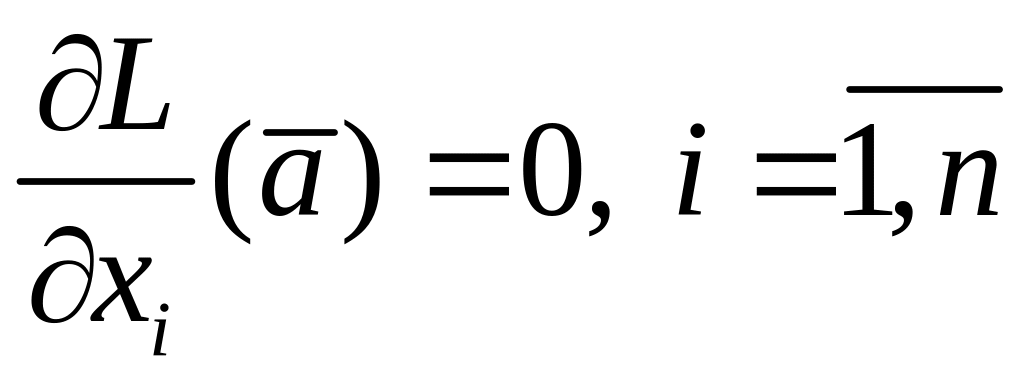, а условия (8) – в виде .

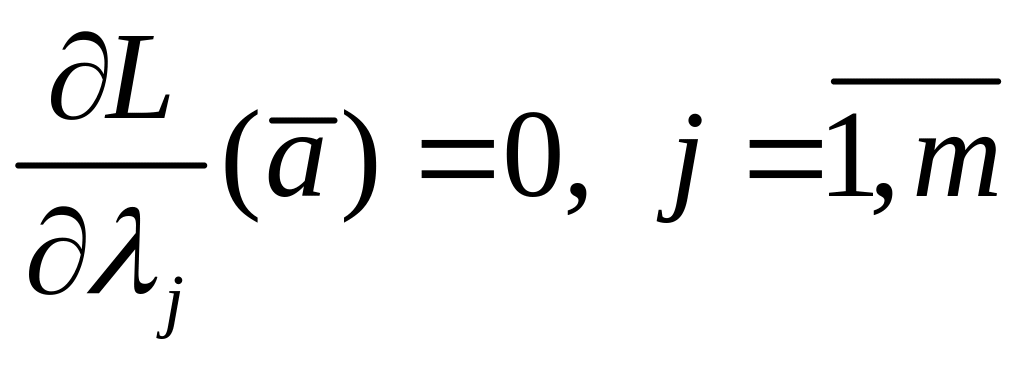Точка , в которой выполняются условия (7) и (8) называется стационарной точкой функции Лагранжа.

В заключение сформулируем достаточное условие существования условного экстремума.

Пусть функции и являются дважды дифференцируемыми на . Пусть – стационарная точка функции Лагранжа. В точке выполняются условия 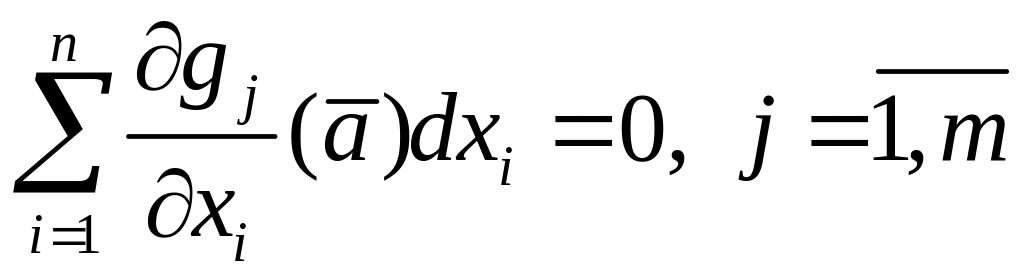, (10)

которые получаются формальным дифференцированием уравнений связи (1). Из условия (2) следует, что систему (10) можно разрешить относительно :

.

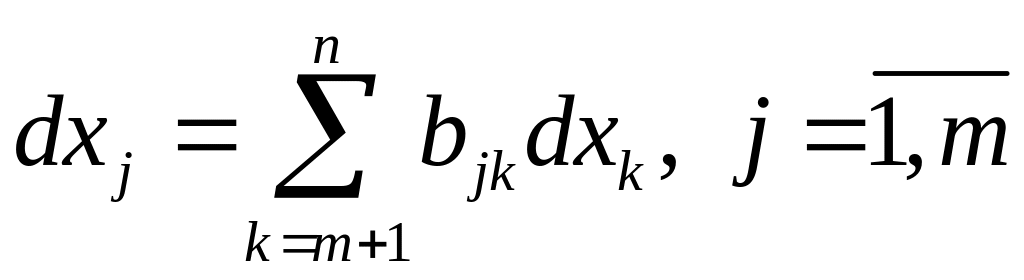После подставления этих выражений во второй дифференциал функции Лагранжа, вычисленный в точке , получим квадратичную форму относительно :

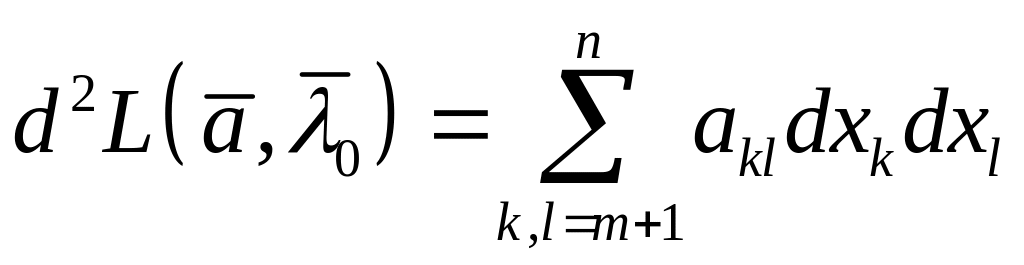. (11)

Имеет место следующее утверждение:

если квадратичная форма (11) является положительно (отрицательно) определённой, то точка есть точка условного минимума (максимума) функции при связях (1).

Отметим, что в конкретных задачах множители Лагранжа имеют содержательную интерпретацию. Так в механике множители Лагранжа задают реакции связей, в математической экономике – цены продуктов производства.