
- •Глава 8. Неявные функции. §8.1. Существование неявной функции.
- •§8.2. Система неявных функций.
- •§8.3. Зависимость функций.
- •Теорема 1 (необходимое условие зависимости). Если система функций зависима на , то ранг матрицы Якоби меньше, чем в каждой точке .
- •Теорема 2 (достаточное условие независимости). Если хотя бы в одной точке ранг матрицы Якоби (2) равен , то система функций независима на .
- •Пример 2. Пользуясь теоремой 3, исследуем на зависимость систему функций .
- •§8.4. Условный экстремум.
- •Пример 1 Найти экстремум функции при условии .
- •Пример 2. Пусть задана точка . Найдём расстояние от до плоскости (12)
§8.3. Зависимость функций.
Пусть функции
![]() непрерывно
дифференцируемы в области
непрерывно
дифференцируемы в области
![]() .
.
def.
Функцию
![]() называют
зависимой
от
функций
называют
зависимой
от
функций
![]() на множестве
,
если существует непрерывно
дифференцируемая функция
на множестве
,
если существует непрерывно
дифференцируемая функция
![]() такая, что
такая, что
![]() .
(1)
.
(1)
def.
Система
функций
![]() называется зависимой
на множестве
,
если хотя
бы одна
из
них
зависит
от остальных
на
.
Если же
ни одна
из
функций
не зависит
от остальных,
то такую систему
функций называют
независимой
на
.
называется зависимой
на множестве
,
если хотя
бы одна
из
них
зависит
от остальных
на
.
Если же
ни одна
из
функций
не зависит
от остальных,
то такую систему
функций называют
независимой
на
.
Пример 1. Рассмотрим функции .
Поскольку , то , т.е. существует функция такая, что . Таким образом, система функций является зависимой.
def. Прямоугольную матрицу (2)
называют матрицей Якоби.
Изучим условия зависимости и независимости системы функций.
Теорема 1 (необходимое условие зависимости). Если система функций зависима на , то ранг матрицы Якоби меньше, чем в каждой точке .
□ Если , а – ранг матрицы Якоби, то .
Пусть
![]() .
Поскольку
– зависимы
на
,
тогда
одна
из
функций, например
,
зависит
от остальных,
т.е. имеет
место
(1).
Вычислим
частные
производные
.
Поскольку
– зависимы
на
,
тогда
одна
из
функций, например
,
зависит
от остальных,
т.е. имеет
место
(1).
Вычислим
частные
производные
 как
сложной
функции из
(1).
Имеем
как
сложной
функции из
(1).
Имеем
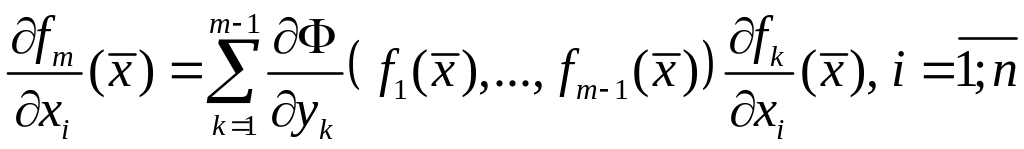 .
.
Это
равенство
означает,
что последняя
строка
матрицы
Якоби (2) есть
линейная комбинация
первых
![]() строк:
строк:
![]()
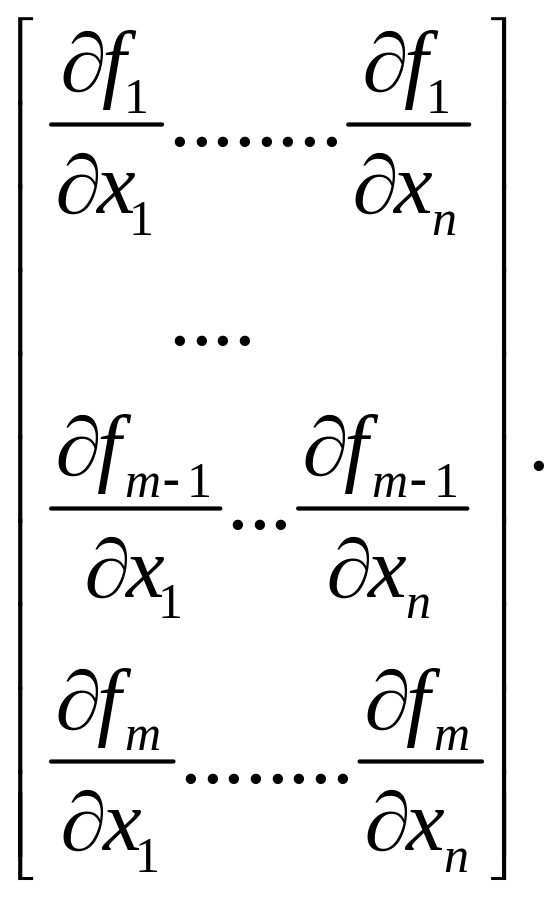
Поэтому
все определители
–
го
порядка
равны
нулю, т.е. ранг матрицы
Якоби
![]() .
■
.
■
Теорема 2 (достаточное условие независимости). Если хотя бы в одной точке ранг матрицы Якоби (2) равен , то система функций независима на .
□ (от противного) Если допустить зависимость этой системы функций, то в соответствии с теоремой 1 ранг матрицы Якоби (2) меньше, чем во всех точках области . Но это невозможно, поскольку в точке ранг матрицы Якоби равен ?!? (пришли к противоречию). ■
Теорема 3
(достаточное
условие зависимости).
Пусть
функции
![]() непрерывно дифференцируемы в окрестности
непрерывно дифференцируемы в окрестности
![]() и ранг матрицы Якоби
и ранг матрицы Якоби
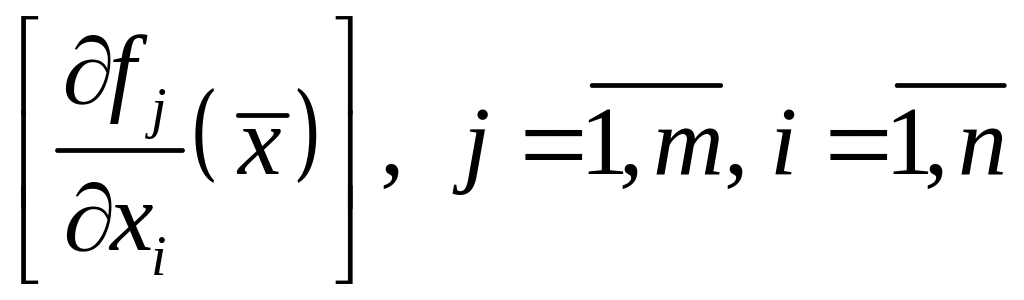 в точке
в точке
![]() равен
равен
![]() ,
причём
,
причём
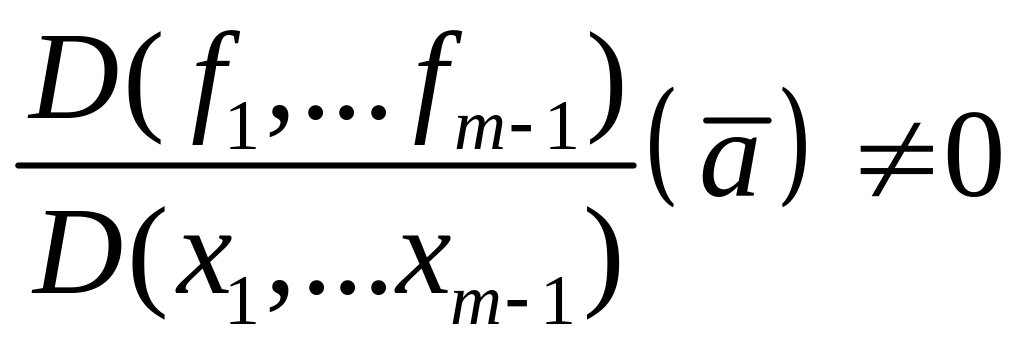 .
Тогда в достаточно малой окрестности
.
Тогда в достаточно малой окрестности
![]() функция
зависит от функций
,
которые
независимы
в этой окрестности, т.е.
функция
зависит от функций
,
которые
независимы
в этой окрестности, т.е.
![]() имеют место равенства (1).
имеют место равенства (1).
□ Независимость
функций
в
![]() следует
из
теоремы
2.
следует
из
теоремы
2.
Согласно
теореме
3 §8.2
система
уравнений
![]() разрешима
относительно переменных
и имеет
единственное
решение
разрешима
относительно переменных
и имеет
единственное
решение
![]() в
окрестности точки
в
окрестности точки
![]() ,
причём
функции
,
причём
функции
![]() являются непрерывно
дифференцируемыми,
и имеют
место
тождества
являются непрерывно
дифференцируемыми,
и имеют
место
тождества
![]() ,
(3)
,
(3)
![]() ,
(4)
,
(4)
Дифференцируя
тождества
(3) по
переменным
![]() ,
получим
,
получим
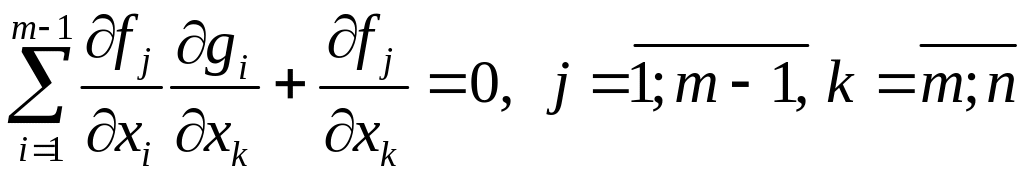 (5)
(5)
Поскольку функции непрерывно дифференцируемые, то функция
![]() (6)
(6)
как композиция является непрерывно дифференцируемой.
Остаётся
доказать,
что функция
![]() не зависит
явно от
переменных
не зависит
явно от
переменных
![]() .
Для этого
достаточно
доказать,
что
.
Для этого
достаточно
доказать,
что
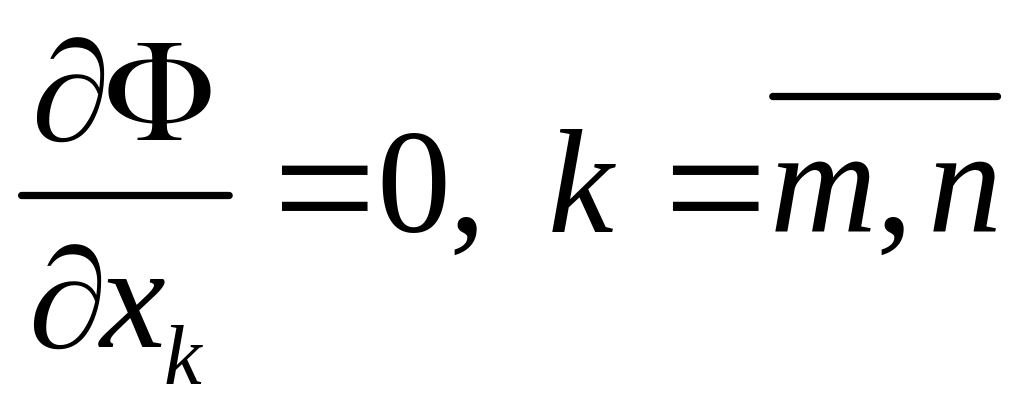 .
.
Убедимся
в том, что
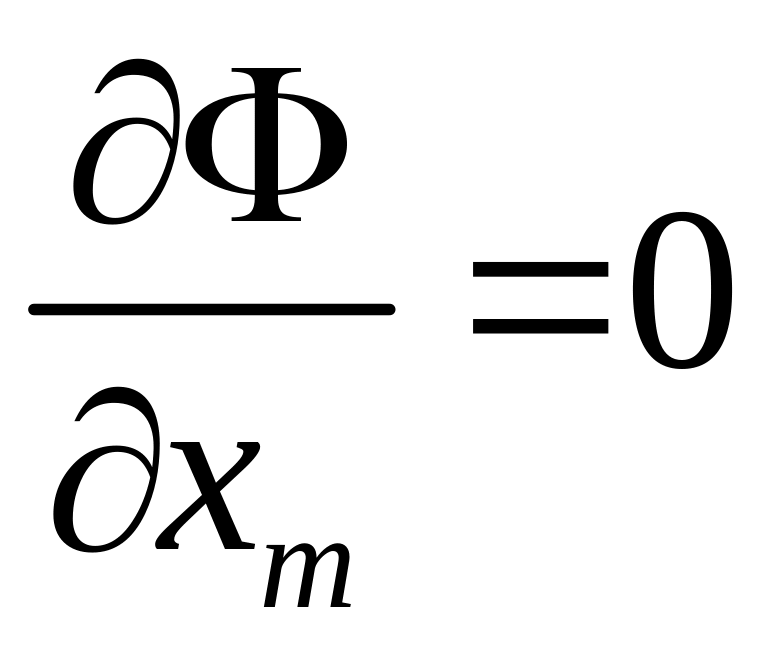 .
Продифференцируем
функцию
из
равенства
(6) по
переменной
.
Продифференцируем
функцию
из
равенства
(6) по
переменной
![]() как
сложную
функцию
как
сложную
функцию
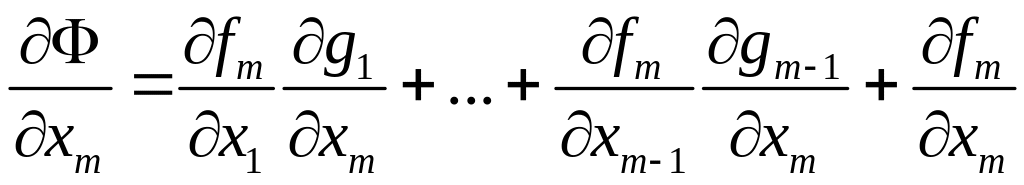 .
(7)
.
(7)
Рассмотрим следующий минор порядка матрицы Якоби:
![]()
 .
(8)
.
(8)
Поскольку ранг
матрицы
Якоби равен
,
то
![]() .
Умножим
первые
столбцов
матрицы
.
Умножим
первые
столбцов
матрицы
![]() соответственно
на
соответственно
на
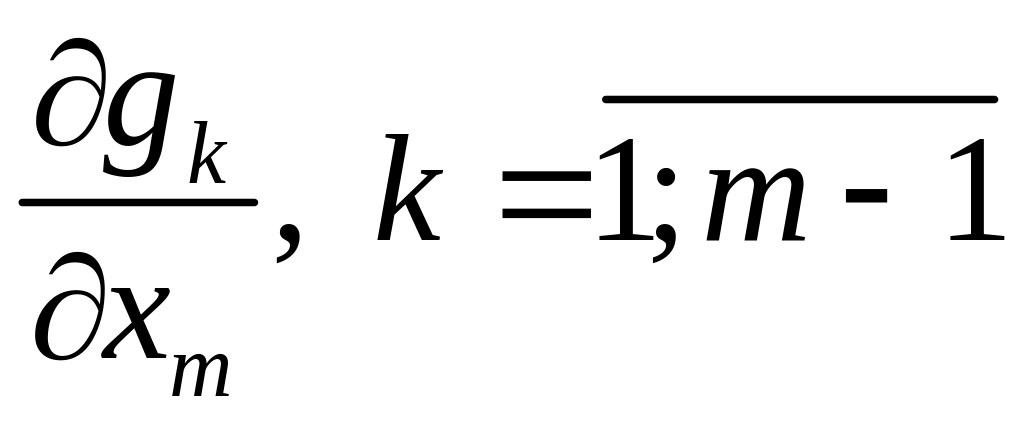 и прибавим
их к последнему столбцу.
Поскольку первые
элементов
последнего
столбца
из
(8) станут
равными
(5) (при
и прибавим
их к последнему столбцу.
Поскольку первые
элементов
последнего
столбца
из
(8) станут
равными
(5) (при
![]() ),
т.е. равными
нулю, а последний
элемент как
раз является
),
т.е. равными
нулю, а последний
элемент как
раз является
![]() из
(7), и матрица
принимает
вид
, то . Поскольку
из
(7), и матрица
принимает
вид
, то . Поскольку
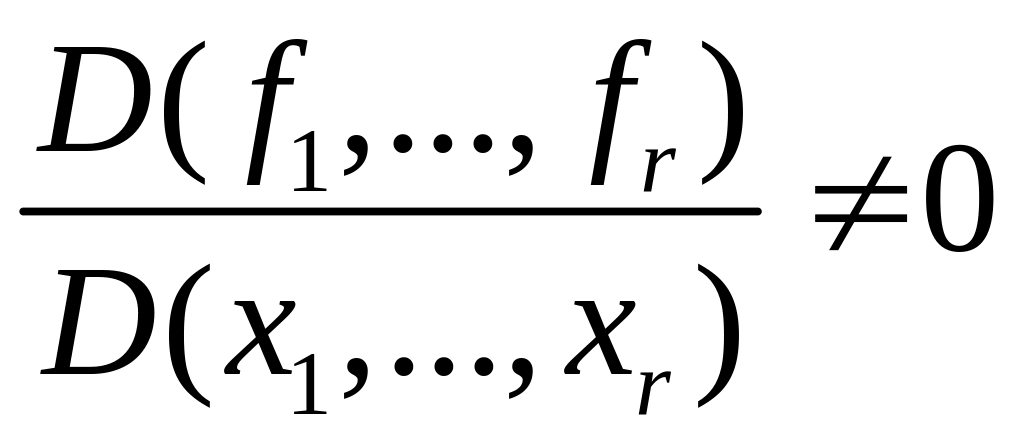 ,
то
,
то
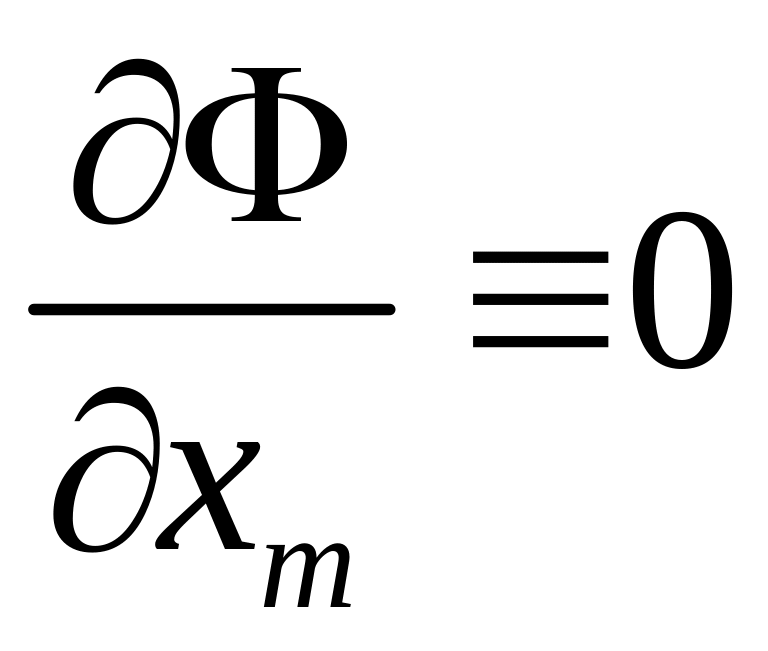 .
Аналогично
получается,
что
.
Аналогично
получается,
что
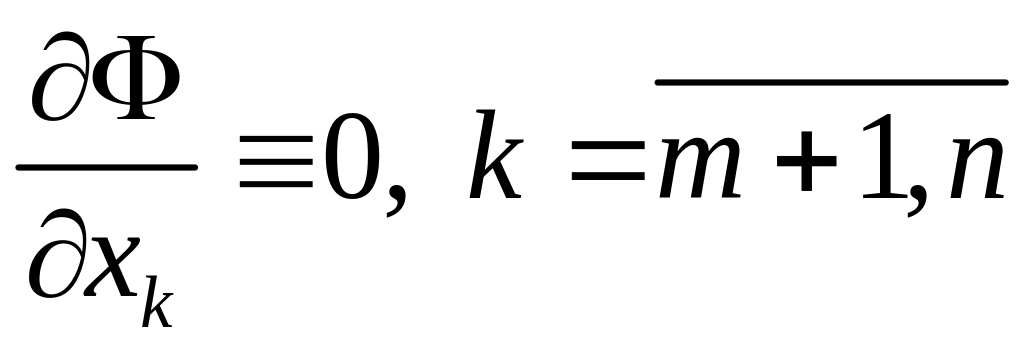 .
.
Таким образом,
функция
из
(6) не зависит
от переменных
![]() и поэтому
функция
и поэтому
функция
![]() ,
т.е. функция
,
т.е. функция
![]() зависит
от
зависит
от
![]() .
■
.
■
Из этой теарэмы непосредственно получается
Следствие.
Пусть функции
![]() являются
непрерывно
дифференцируемыми
в некоторай
окрестности
и при каждом
являются
непрерывно
дифференцируемыми
в некоторай
окрестности
и при каждом
![]() ранг матрицы
Якоби
ранг матрицы
Якоби
![]() равен
.
Тогда среди
функций
существуют
равен
.
Тогда среди
функций
существуют
![]() независимых
в
окрестности
функций, а каждая
из
остальных
независимых
в
окрестности
функций, а каждая
из
остальных
![]() функций зависит
в
этой
окрестности от указанных
функций.
функций зависит
в
этой
окрестности от указанных
функций.
