Глава 8. Неявные функции. §8.1. Существование неявной функции.

Пусть функция определена на некатором множестве из . Рассмотрим уравнение . (1)

Множество точек плоскости, координаты которых удовлетворяют уравнению (1), называют графиком уравнения (1).

Так графиком уравнения является окружность, а уравнения – пара прямых.

Пусть проекцией графика уравнения (1) на ось является множество .

Если график уравнения (1) взаимно однозначно проектируется на ось , то существует единственная функция , график которой совпадает с графиком уравнения. Эта функция ставит в соответствие каждому то единственное значение , для которого , т.е. . При этом говорят, что уравнение (1) определяет как неявную функцию от .

Но обычно график уравнения (1) проек- тируется неоднозначно на , например, . Тогда на , вобще говоря, определяется бесконечномного функций, графики которых совпадают с некоторым подмножеством графика .

Пусть график уравнения (1) проектируется неоднозначно на , но существует такой прямоугольник , что часть графика , расположенная внутри , взаимно однозначно проектируется на . Тогда на определена функция , которая каждому ставит в соответствие единственное значение , т.е. .

def. Если существует функция , определённая на , такая что , то будем говорить, что функция неявно определяется уравнением (1) в прямоугольнике , или, что уравнение (1) определяет в прямоугольнике переменную как неявную функцию от переменной .

Так уравнение на прямоугольнике определяет неявно функцию , а на прямоугольнике – функцию .

Меняя ролями и , можно говорить о неявной функции , которая определяется также уравнением (1).

На основании этих геометрических рассуждений сформулируем теорему, выражающую достаточные условия существования, непрерывности и дифференцируемости неявной функции.

Теорема 1 (о существовании неявной функции). Пусть функция из (1) имеет непрерывные частные производные в некоторой окрестности точки , причём . Тогда существует прямо-угольник , в котором уравнение (1) определяет как неявную функцию переменной , . При этом функция имеет непрерывную производную на интервале и . (2)

(Без доказательства)

def. Если существует функция такая, что , то говорят, что уравнение (3)

определяет как функцию переменных . Здесь – подмножество проекции графика уравнения (3) на плоскость .

Покажем, как вычисляются частные производные неявной функции двух переменных. Пусть уравнение определяет неявную функцию , т.е. , а поэтому . На основании свойства инвариантности первого дифференциала имеем

,

откуда следует 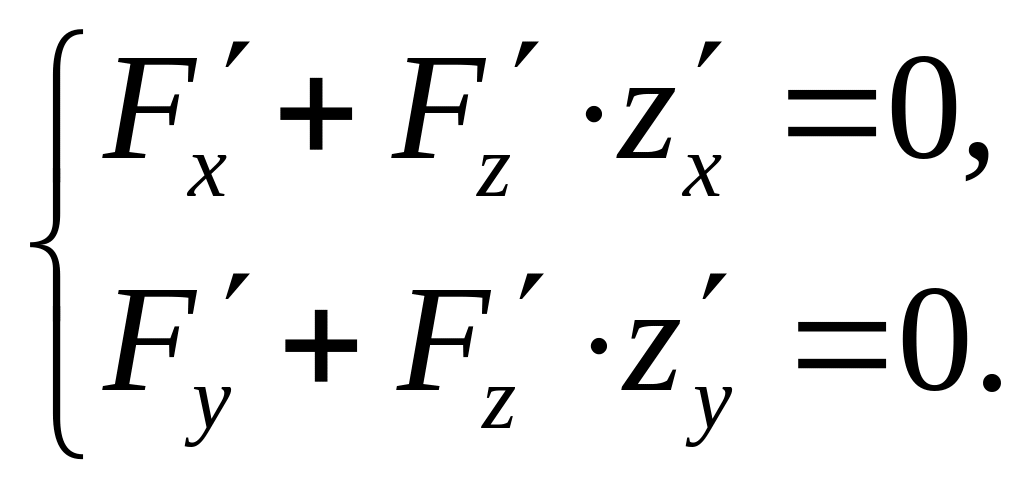Из этой системы получаем .

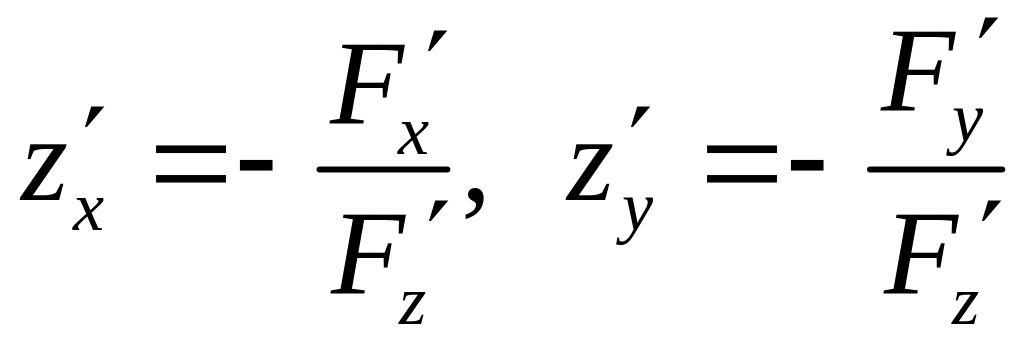Далее вычислим, например,

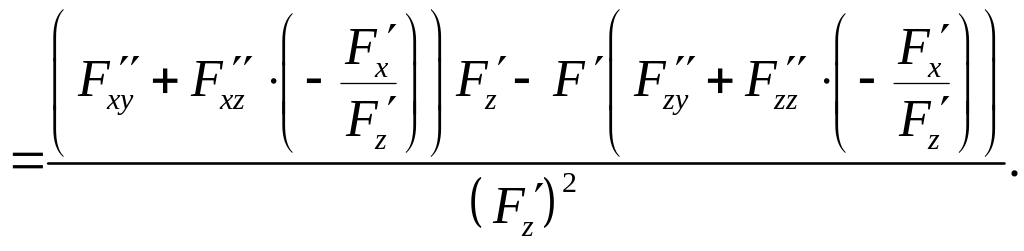
Теорема 2 (о существовании неявной функции нескольких переменных). Пусть функция имеет непрерывные частные производные в некоторой окрестности точки , причём а . Тогда существует окрестность точки , в которой уравнение определяет как неявную функцию переменной , . При этом функция имеет в некоторой окрестности точки непрерывные частные производные и .