
- •1.Матрицы. Основные понятия. Прямоугольная таблица:
- •2.Действия над матрицами.
- •3.Обратная матрица. Пример.
- •7.Линейные операции над векторами.
- •8.Скалярное произведение векторов. Свойства.
- •12.Смешанное произведение векторов.
- •13.Функция. Основные понятия.
- •14.Пределы числовой последовательности.
- •17.Бесконечно малые функции и их свойства.
- •18. Бесконечно-большие функции и их свойства.
- •19. Основные теоремы о пределах.
- •20. Первый замечательный предел.
- •21. Второй замечательный предел.
- •23.Точки разрыва.
- •26.Таблица производных.
- •27.Основные прав ила дифференцирования.
- •Производная обратной функции
- •29.Дифференциал функции и его основные свойства.
- •30. Теоремы о дифференцируемых функциях.
- •31.Правило Лопиталя.
- •Существует конечный или бесконечный предел . Тогда: .
- •35.Прямая на плоскости. Способы задания.
- •36. Плоскость. Способы задания.
- •38.Взаимное расположение прямых.
- •39.Эллипс и его характеристики.
- •40. Гипербола.
- •44.Таблица интегралов.
- •48.Интегрирование по частям.
- •50.Интегрирование иррациональных функций. Если рациональная функция своих аргументов, а целые положительные числа, то интеграл:
- •Вычисление
- •58.Длина дуги.
Производная обратной функции
Пусть
функция
задана на множестве
,
а
![]() – множество ее значений. Тогда каждому
ставится в соответствие единственное
значение
– множество ее значений. Тогда каждому
ставится в соответствие единственное
значение
![]() .
С другой стороны, каждому
будет соответствовать одно или несколько
значений
.
В случае, когда отображение
является биективным, т.е. каждому значению
соответствует только одно значение
,
для которого
.
С другой стороны, каждому
будет соответствовать одно или несколько
значений
.
В случае, когда отображение
является биективным, т.е. каждому значению
соответствует только одно значение
,
для которого
![]() ,
на множестве
можно определить функцию
,
на множестве
можно определить функцию
![]() ,
множеством значений которой является
,
которая будет называться обратной по
отношению к функции
.
Функции
и
называются взаимообратными.
,
множеством значений которой является
,
которая будет называться обратной по
отношению к функции
.
Функции
и
называются взаимообратными.
Пусть
функция
удовлетворяет условиям существования
обратной функции и в точке
![]() имеет конечную производную
имеет конечную производную
![]() .
Тогда обратная функция
в точке
.
Тогда обратная функция
в точке
![]() также имеет конечную производную, равную
также имеет конечную производную, равную
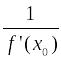 .
.
29.Дифференциал функции и его основные свойства.
Дифференцируемость
функции
в точке
![]() означает, что ее приращение представимо
в виде:
означает, что ее приращение представимо
в виде:
![]() .
.
Величина
![]() при малых
при малых
![]() мала по сравнению с величиной
.
Поэтому
мала по сравнению с величиной
.
Поэтому
![]() представляет собой главную часть
приращения
представляет собой главную часть
приращения
![]() ,
называемую дифференциалом
функции
в точке
.
Дифференциал функции
обозначают обычно символами:
,
называемую дифференциалом
функции
в точке
.
Дифференциал функции
обозначают обычно символами:
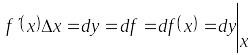 и др.
и др.
Если
‑ независимая переменная, то
![]() и поэтому
и поэтому
![]() .
.
Вычисление
дифференциалов проводят по правилам 1
‑ 6 дифференцирования с заменой
символа
(штрих) на символ
![]() .
Например:
.
Например:
![]() ;
;
![]() .
.
Таким
образом, приращение функции
![]() в точке
в точке
![]() при малых значениях
приблизительно в пять раз больше, чем
,
а приращение функции в точке
при малых значениях
приблизительно в пять раз больше, чем
,
а приращение функции в точке
![]() приблизительно в 14 раз больше, чем
.
приблизительно в 14 раз больше, чем
.
30. Теоремы о дифференцируемых функциях.
Теорема
Ферма. Если
функция
![]() дифференцируема в точке
,
т.е. существует
дифференцируема в точке
,
т.е. существует
![]() ,
и всюду в некоторой окрестности этой
точки
,
и всюду в некоторой окрестности этой
точки
![]()
![]() ,
т.е.
,
т.е.
![]() является наибольшим (наименьшим)
значением функции в этой окрестности,
то
является наибольшим (наименьшим)
значением функции в этой окрестности,
то
![]() .
.
Теорема
Ролля. Если
функция
непрерывна на отрезке
,
дифференцируема на интервале
и
![]() ,
то в некоторой точке интервала
,
то в некоторой точке интервала
![]() ее
производная равна нулю.
ее
производная равна нулю.
Геометрический смысл теоремы Ролля заключается в том, что в найдется точка, в которой касательная к кривой будет горизонтальна.
Теорема
Лагранжа. Если
функция
непрерывна на отрезке
,
дифференцируема на интервале
,
то найдется точка
для которой
![]() .
.
Следствие.
Теорема
Лагранжа является обобщением теоремы
Ролля для случая
.
Тогда
![]() .
.
Теорема
Коши.
Если функции
и
![]() определены и непрерывны на отрезке
,
дифференцируемы на интервале
и при этом
определены и непрерывны на отрезке
,
дифференцируемы на интервале
и при этом
![]() ,
то найдется точка
,
для которой
,
то найдется точка
,
для которой
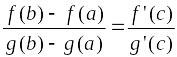 .
.
31.Правило Лопиталя.
Пусть
![]() и
и
![]() - функции, определенные и дифференцируемые
в окрестности точки a,
где a
- конечное число или
- функции, определенные и дифференцируемые
в окрестности точки a,
где a
- конечное число или
![]() (если
(если
![]() ,
то под окрестностью точки a
понимаем какой-нибудь луч
,
то под окрестностью точки a
понимаем какой-нибудь луч
![]() ;
если
;
если
![]() ,
то окрестность – луч
,
то окрестность – луч
![]() ).
В самой точке a
функции могут быть не определены. Пусть
).
В самой точке a
функции могут быть не определены. Пусть
![]() при
при
![]() .
.
I правило. Если:
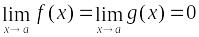
Существует конечный или бесконечный предел . Тогда: .
II правило. Если:
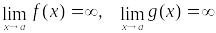 ;
;Существует конечный или бесконечный предел
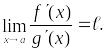 Тогда:
.
Тогда:
.
Правила
Лопиталя позволяют раскрывать
неопределенности вида
![]() или
или
![]() .
Однако, они могут быть использованы и
при раскрытии неопределенностей других
видов:
.
Однако, они могут быть использованы и
при раскрытии неопределенностей других
видов:
![]() .
Для этого исследуемое выражение
преобразуют так, чтобы получилась
неопределенность вида
или
.
Для этого исследуемое выражение
преобразуют так, чтобы получилась
неопределенность вида
или
![]() .
.
32.Исследование
на монотонность. Точки экстремума.
.
Функция
![]() называется возрастающей
на промежутке
называется возрастающей
на промежутке
![]() ,
если
,
если
![]() для любых точек
для любых точек
![]() и
и
![]() из промежутка
,
удовлетворяющих неравенству
из промежутка
,
удовлетворяющих неравенству
![]() .
Функция называется убывающей
на
,
если из условия
следует
.
Функция называется убывающей
на
,
если из условия
следует
![]() .
.
Теорема.
Если функция
непрерывна на отрезке
,
дифференцируема на интервале
,
то для того, чтобы
была возрастающей (убывающей) необходимо
и достаточно, чтобы
![]()
![]() в каждой внутренней точке интервала
.
в каждой внутренней точке интервала
.
Дифференцируемая
функция является возрастающей на
промежутке
тогда и только тогда, когда
![]() .
.
Локальный экстремум
Точка
называется точкой локального
максимума
функции
![]() ,
если существует интервал
,
если существует интервал
![]() ,
содержащий точку
такой что
,
содержащий точку
такой что
![]() .
.
Точка
называется точкой локального
минимума
функции
,
если существует интервал
,
содержащий точку
такой что
![]() .
.
Точки локального минимума и локального максимума называются точками локального экстремума.
Необходимым
условием локального экстремума
дифференцируемой функции является
выполнение равенства
![]() .
Поэтому точки, в которых дифференцируемая
функция может иметь локальный экстремум,
находят, решая уравнение:
.
.
Поэтому точки, в которых дифференцируемая
функция может иметь локальный экстремум,
находят, решая уравнение:
.
Решения этого уравнения называют стационарными точками.
Исследование стационарных точек
I
правило.
Если при возрастании
при переходе через стационарную точку
производная
![]() меняет знак с +
на ‑
, то
‑ точка локального максимума. Если
меняет знак с ‑
на +
, то
‑ точка локального минимума функции
меняет знак с +
на ‑
, то
‑ точка локального максимума. Если
меняет знак с ‑
на +
, то
‑ точка локального минимума функции
![]() .
Если
.
Если
![]() не меняет знак в точке
,
то экстремума нет.
не меняет знак в точке
,
то экстремума нет.
II
правило.
Если вторая производная
![]() в стационарной точке
положительная, то
‑ точка локального минимума функции
.
Если вторая производная
в стационарной точке
отрицательная, то
‑ точка локального максимума функции
.
в стационарной точке
положительная, то
‑ точка локального минимума функции
.
Если вторая производная
в стационарной точке
отрицательная, то
‑ точка локального максимума функции
.
Точками локального экстремума функции могут быть такие точки, в которых производная не существует или обращается в бесконечность. Исследовать такие точки можно по I правилу. Экстремум в такой точке называется острым экстремумом.
Глобальный
экстремум.Непрерывная
на отрезке
![]() функция
функция
![]() принимает свое наибольшее значение
принимает свое наибольшее значение
![]() и свое наименьшее значение
и свое наименьшее значение
![]() в точках этого отрезка. Эти значения
могут достигаться либо в стационарных
точках отрезка, либо в точках
недифференцируемости функции, либо в
граничных точках отрезка. Поэтому для
нахождения значений
и
поступают следующим образом.
в точках этого отрезка. Эти значения
могут достигаться либо в стационарных
точках отрезка, либо в точках
недифференцируемости функции, либо в
граничных точках отрезка. Поэтому для
нахождения значений
и
поступают следующим образом.
Находят стационарные точки
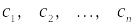 функции;
функции;Находят точки
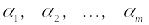 ,
в которых производная
не существует или обращается в
бесконечность;
,
в которых производная
не существует или обращается в
бесконечность;Вычисляют значения:
![]() ‑ и выбирают
среди этих чисел наибольшее и наименьшее.
‑ и выбирают
среди этих чисел наибольшее и наименьшее.
Это и будут и ‑ глобальные экстремальные значения.
33.Выпуклость,
вогнутость. Точки перегиба.
Графиком функции
,
заданной на множестве
,
называют множество точек плоскости с
координатами![]() .
График называют выпуклым
вниз на
промежутке
,
если касательная к графику в любой точке
этого промежутка расположена ниже
графика. Если касательная расположена
выше графика, то график называют выпуклым
вверх. Точка,
в которой график меняет направление
выпуклости, называется точкой
перегиба.
.
График называют выпуклым
вниз на
промежутке
,
если касательная к графику в любой точке
этого промежутка расположена ниже
графика. Если касательная расположена
выше графика, то график называют выпуклым
вверх. Точка,
в которой график меняет направление
выпуклости, называется точкой
перегиба.
Если на промежутке
вторая производная
![]() положительна, то график является выпуклым
вниз на этом промежутке. Если
положительна, то график является выпуклым
вниз на этом промежутке. Если
![]() на промежутке
,
то график является выпуклым вверх на
промежутке
.
на промежутке
,
то график является выпуклым вверх на
промежутке
.
Точка
![]() может быть точкой перегиба только в том
случае, когда
может быть точкой перегиба только в том
случае, когда
![]() ,
либо
,
либо
![]() не существует – необходимое условие
перегиба. Однако равенство нулю или не
существование второй производной в
точке
не означает еще, что в точке
не существует – необходимое условие
перегиба. Однако равенство нулю или не
существование второй производной в
точке
не означает еще, что в точке
![]() будет перегиб графика. Поэтому нужно
дополнительно исследовать такие точки.
будет перегиб графика. Поэтому нужно
дополнительно исследовать такие точки.
I правило. Если равна нулю или не существует и при переводе через точку меняет знак, то ‑ точка перегиба графика функции .
II
правило.
Если
и
![]() ,
то
,
то
![]() является точкой перегиба графика функции
.
является точкой перегиба графика функции
.
34.Ассимптоты.
Находят точки разрыва и промежутки, на
которых она непрерывна. Выясняют характер
точек разрыва. Вычисляют предельные
значения функции в граничных точках
множества
(если таковые имеются). Находят вертикальные
асимптоты
(в точках бесконечного
скачка). Если
не ограничено, то вычисляют пределы
функции при
![]() и
и
![]() .
Если
.
Если
![]() ,
то график имеет горизонтальную
левостороннюю асимптоту
,
то график имеет горизонтальную
левостороннюю асимптоту
![]() ,
если
,
если
![]() ,
график имеет горизонтальную правостороннюю
асимптоту
,
график имеет горизонтальную правостороннюю
асимптоту
![]() .
Если пределы (или один из пределов)
бесконечны, то график может иметь
наклонные (левостороннюю и правостороннюю)
асимптоты
.
Если пределы (или один из пределов)
бесконечны, то график может иметь
наклонные (левостороннюю и правостороннюю)
асимптоты
![]() .
Коэффициенты левосторонней асимптоты
можно найти по формулам:
.
Коэффициенты левосторонней асимптоты
можно найти по формулам:
![]() .
.
Аналогично находят коэффициенты правосторонней асимптоты (нужно вычислить пределы при ).
Вычисляют производную . Находят критические точки функции , т.е. стационарные точки и точки, в которых не существует. Выделяют промежутки, на которых сохраняет знак. Это позволяет исследовать монотонность функции .
