
- •1.Матрицы. Основные понятия. Прямоугольная таблица:
- •2.Действия над матрицами.
- •3.Обратная матрица. Пример.
- •7.Линейные операции над векторами.
- •8.Скалярное произведение векторов. Свойства.
- •12.Смешанное произведение векторов.
- •13.Функция. Основные понятия.
- •14.Пределы числовой последовательности.
- •17.Бесконечно малые функции и их свойства.
- •18. Бесконечно-большие функции и их свойства.
- •19. Основные теоремы о пределах.
- •20. Первый замечательный предел.
- •21. Второй замечательный предел.
- •23.Точки разрыва.
- •26.Таблица производных.
- •27.Основные прав ила дифференцирования.
- •Производная обратной функции
- •29.Дифференциал функции и его основные свойства.
- •30. Теоремы о дифференцируемых функциях.
- •31.Правило Лопиталя.
- •Существует конечный или бесконечный предел . Тогда: .
- •35.Прямая на плоскости. Способы задания.
- •36. Плоскость. Способы задания.
- •38.Взаимное расположение прямых.
- •39.Эллипс и его характеристики.
- •40. Гипербола.
- •44.Таблица интегралов.
- •48.Интегрирование по частям.
- •50.Интегрирование иррациональных функций. Если рациональная функция своих аргументов, а целые положительные числа, то интеграл:
- •Вычисление
- •58.Длина дуги.
23.Точки разрыва.
Непрерывность
функции
в точке
,
т.е. выполнение условия (3), означает, что
оба односторонних предела
и
существуют и равны
![]() ,
т.е.
,
т.е.
![]() .
.
Если условие (4) не выполнено, то точку называют точкой разрыва функции . Условие (4) означает выполнение следующих четырех условий, каждое из которых предполагает выполнение всех предыдущих:
и существуют;
и конечны;
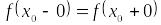 ;
;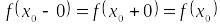 .
.
Если 1. не выполнено, то называют точкой неопределенности.
Если 1. выполнено, а 2. не выполнено, то называют точкой бесконечного скачка.
Если
выполнены 1. и 2., а 3. не выполнено, то
называют точкой
конечного скачка.
Величина
![]() называется скачком функции
в точке
.
называется скачком функции
в точке
.
Если 1., 2., 3. выполнены, а 4. не выполнено, то называют точкой устранимого разрыва.
Если функция определена в окрестности точки и не определена в самой точке , то также называют точкой разрыва. Такие точки классифицируют по той же схеме.
24.Свойства
непрерывных функций на отрезке.Функция
,
определенная на отрезке
![]() (
(![]() )
называется непрерывной
на отрезке
,
если она непрерывна в каждой точке
интервала
)
называется непрерывной
на отрезке
,
если она непрерывна в каждой точке
интервала
![]() ,
непрерывна справа в точке
,
непрерывна справа в точке
![]() и непрерывна слева в точке
.
и непрерывна слева в точке
.
Общие свойства непрерывных функций, заданных на отрезке , определяются четырьмя теоремами: двумя теоремами Больцано–Коши и двумя теоремами Вейерштрасса.
Теорема
(первая теорема Больцано–Коши).
Пусть
функция
определена и непрерывна на отрезке
,
и на концах этого промежутка принимает
значения разных знаков; тогда найдется
точка
![]() ,
в которой функция равна нулю.
,
в которой функция равна нулю.
Теорема
(вторая теорема Больцано–Коши).
Пусть
функция
определена и непрерывна на отрезке
.
Тогда, если
![]() то функция принимает все свои промежуточные
значения, принадлежащие промежутку
то функция принимает все свои промежуточные
значения, принадлежащие промежутку
![]() ,
где
,
где
![]() ,
,
![]() ,
т.е.
,
т.е.
![]() .
.
Теорема (первая теорема Вейерштрасса). Пусть функция определена и непрерывна на отрезке , тогда функция является ограниченной на этом отрезке.
Теорема (вторая теорема Вейерштрасса). Пусть функция определена и непрерывна на отрезке , тогда функция имеет минимум и максимум на этом отрезке (множество значений функции включает в себя точные верхнюю и нижнюю границы).
25.Производная. ЕЕ геометрический и физический смысл.Касательной графика функции проведенную через (·)М0(x0;y0) назыв. предельное положение сек. при…….
Если рассматривать физические процессы,то производная характеризует скорость изменения тех или иных физических процессов.
26.Таблица производных.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27.Основные прав ила дифференцирования.
Функция
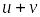 дифференцируема и
дифференцируема и
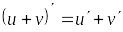 ;
;Если
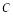 ‑ постоянная, то функция
‑ постоянная, то функция
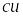 дифференцируема и
дифференцируема и
 ;
;Из 1 и 2 следует, что
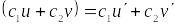 ;
;Функция
 дифференцируема и
дифференцируема и
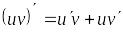 ;
;Из 4 следует, что
 ;
;Если
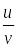 определена и дифференцируема, то
определена и дифференцируема, то
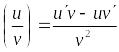 .
.
28.Производная
сложной и обратной функции. Производная
сложной функции.
Пусть
![]() и
и
![]() .
Тогда можно определить сложную функцию
.
Тогда можно определить сложную функцию
![]() .
Если функция
.
Если функция
![]() дифференцируема в точке
дифференцируема в точке
![]() ,
а функция
дифференцируема в точке
,
а функция
дифференцируема в точке
![]() ,
то сложная функция
,
то сложная функция
![]() дифференцируема в точке
,
и ее производная может быть вычислена
по правилу
цепочки:
дифференцируема в точке
,
и ее производная может быть вычислена
по правилу
цепочки:
 .
.
Или
более кратко
![]() .
.
Правило
можно записать также в виде:
![]() .
.

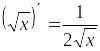
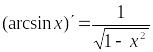 ;
;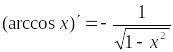 .
.