
- •1.Матрицы. Основные понятия. Прямоугольная таблица:
- •2.Действия над матрицами.
- •3.Обратная матрица. Пример.
- •7.Линейные операции над векторами.
- •8.Скалярное произведение векторов. Свойства.
- •12.Смешанное произведение векторов.
- •13.Функция. Основные понятия.
- •14.Пределы числовой последовательности.
- •17.Бесконечно малые функции и их свойства.
- •18. Бесконечно-большие функции и их свойства.
- •19. Основные теоремы о пределах.
- •20. Первый замечательный предел.
- •21. Второй замечательный предел.
- •23.Точки разрыва.
- •26.Таблица производных.
- •27.Основные прав ила дифференцирования.
- •Производная обратной функции
- •29.Дифференциал функции и его основные свойства.
- •30. Теоремы о дифференцируемых функциях.
- •31.Правило Лопиталя.
- •Существует конечный или бесконечный предел . Тогда: .
- •35.Прямая на плоскости. Способы задания.
- •36. Плоскость. Способы задания.
- •38.Взаимное расположение прямых.
- •39.Эллипс и его характеристики.
- •40. Гипербола.
- •44.Таблица интегралов.
- •48.Интегрирование по частям.
- •50.Интегрирование иррациональных функций. Если рациональная функция своих аргументов, а целые положительные числа, то интеграл:
- •Вычисление
- •58.Длина дуги.
19. Основные теоремы о пределах.
Теорема.
Для
того чтобы последовательность
имела предел, необходимо и достаточно
чтобы
![]() ,
где
– постоянная;
,
где
– постоянная;
![]() –
бесконечно малая.
–
бесконечно малая.
Основные свойства сходящихся последовательностей:
Сходящаяся последовательность имеет только один предел;
Сходящаяся последовательность ограничена;
Если
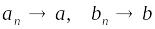 ,
то
,
то
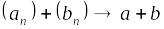 ;
;При любых постоянных и
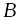
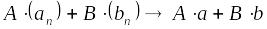 ;
; ;
;Если
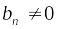 ,
,
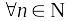 и
и
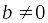 ,
то
,
то
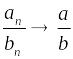 ;
;Если
 ,
то
,
то
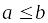 ;
;Если
 и
и
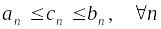 ,
то
,
то
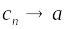 ;
;Если
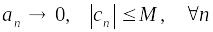 ,
то
,
то
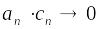 .
.
Свойства 3. и 4. обобщаются на случай любого числа сходящихся последовательностей.
Отметим,
что при вычислении предела дроби,
числитель и знаменатель которой
представляют собой линейные комбинации
степеней
![]() ,
предел дроби равен пределу отношения
старших членов (т.е. членов, содержащих
наибольшие степени
числителя и знаменателя).
,
предел дроби равен пределу отношения
старших членов (т.е. членов, содержащих
наибольшие степени
числителя и знаменателя).
Последовательность
![]() называется:
называется:
возрастающей, если
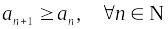 ;
;строго возрастающей, если
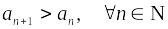 ;
;убывающей, если
 ;
;строго убывающей, если
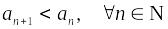 .
.
Все такие последовательности называют монотонными.
Теорема.
Если
последовательность
![]() монотонно возрастает и ограничена
сверху, то она сходится и ее предел равен
ее точной верхней грани; если
последовательность убывает и ограничена
снизу, то она сходится к своей точной
нижней грани.
монотонно возрастает и ограничена
сверху, то она сходится и ее предел равен
ее точной верхней грани; если
последовательность убывает и ограничена
снизу, то она сходится к своей точной
нижней грани.
20. Первый замечательный предел.
Покажем,
что
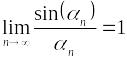
Д ля
простоты примем, что
ля
простоты примем, что
![]() (см. Рис.1.), причем, так как дуга
(см. Рис.1.), причем, так как дуга
![]() стремится к нулю при
стремится к нулю при
![]() ,
то можно считать, что
,
то можно считать, что
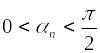 (указанное допущение не является
принципиальным, но позволит использовать
геометрическую интерпретацию). Сравним
величины
(указанное допущение не является
принципиальным, но позволит использовать
геометрическую интерпретацию). Сравним
величины
![]() и
и
![]() с помощью диаграммы, построенной в
первом квадранте.Площади треугольников
с помощью диаграммы, построенной в
первом квадранте.Площади треугольников
![]() ,
,
![]() и сектора
и сектора
![]() соотносятся следующим образом:
соотносятся следующим образом:
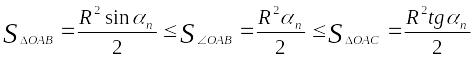
Отсюда
![]() ,
и после деления на
,
и после деления на
![]()
![]() ,
получим
,
получим
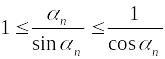 ,
а для обратных величин
,
а для обратных величин
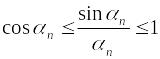 .
Так как при
последовательность
.
Так как при
последовательность
![]() ,
а, следовательно,
,
а, следовательно,
![]() ,
то видно, что последовательность
,
то видно, что последовательность
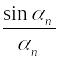 заключена между двумя последовательностями,
имеющими общий предел, равный 1. Таким
образом, можно сделать вывод, что для
бесконечно малой последовательности
заключена между двумя последовательностями,
имеющими общий предел, равный 1. Таким
образом, можно сделать вывод, что для
бесконечно малой последовательности
![]()
![]() ,
справедливо равенство
.
,
справедливо равенство
.
21. Второй замечательный предел.
При
анализе второго замечательного предела
необходимо показать, что последовательность
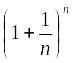 является монотонно возрастающей и
ограниченной сверху. Для этого можно
воспользоваться формулой бинома Ньютона,
положив, что
является монотонно возрастающей и
ограниченной сверху. Для этого можно
воспользоваться формулой бинома Ньютона,
положив, что
![]() ,
а
,
а
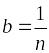 .
Тогда:
.
Тогда:

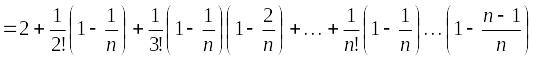 ,
,
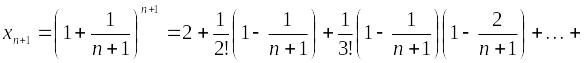
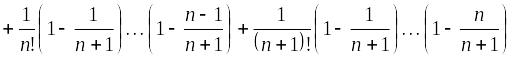 .
.
Таким
образом,
![]()
![]() ,
так как в каждом слагаемом множители
вида
,
так как в каждом слагаемом множители
вида
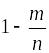 имеют меньшую величину по сравнению с
имеют меньшую величину по сравнению с
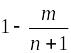 при одном и том же
при одном и том же
![]() ,
а также выражение для
,
а также выражение для
![]() имеет на одно положительное слагаемое
больше.
имеет на одно положительное слагаемое
больше.
Ограниченность
![]() сверху можно показать следующим образом:
сверху можно показать следующим образом:
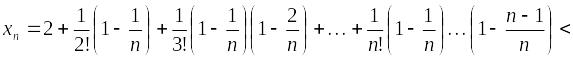
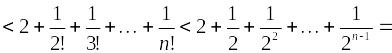
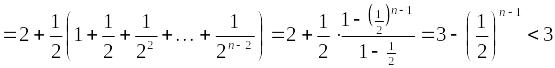 .
.
Таким образом, в соответствии с теоремой о монотонной последовательности имеет предел:
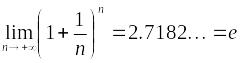 ,
,
который
обозначается
![]() (основание натурального логарифма
(основание натурального логарифма
![]() ).
).
В высшей математике употребляются почти исключительно натуральные логарифмы, поскольку многие формулы для них оказываются более простыми, чем для логарифмов других систем.
22.Неприрывность
функций в точке.
Рассмотрим функцию
![]() ,
определенную на промежутке
,
определенную на промежутке
![]() Пусть
Пусть
![]() .
Функция
называется непрерывной в точке
,
если
.
Функция
называется непрерывной в точке
,
если
![]()
Функция
![]() называется непрерывной
слева (справа)
в точке
,
если
называется непрерывной
слева (справа)
в точке
,
если
![]()
![]() .
Естественно, при этом функция
должна быть определена в некоторой
окрестности слева (справа) то точки
.
Непрерывность функции в точке
означает непрерывность этой функции в
указанной точке как слева, так и справа.
.
Естественно, при этом функция
должна быть определена в некоторой
окрестности слева (справа) то точки
.
Непрерывность функции в точке
означает непрерывность этой функции в
указанной точке как слева, так и справа.
