17.Бесконечно малые функции и их свойства.
Функция
называется бесконечно
малой
при
(или
,
или
)
если для сколь угодно малого положительного
числа
найдется такое положительное число
(
),
что для всех
будет верно неравенство
.
При
(
)
функция
называется бесконечно
малой,
если для сколь угодно малого положительного
числа
найдется такое положительное число
,
что для всех
будет верно неравенство
.
Предел
бесконечно
малой величины
в точке сгущения (или на бесконечности)
равен нулю, т.е.
.
Теорема:
Если
функция
,
определенная на множестве
имеет предел
в точке сгущения
(или на бесконечности), то её можно
представить в виде суммы этого числа и
бесконечно малой величины:
.
Справедлива
также и обратная
теорема:
Если
функцию
,
определенную на множестве
,
можно представить в точке сгущения
(или на бесконечности) в виде суммы
числа
и бесконечно малой величины
:
то число
является пределом этой функции при
указанных условиях.
Свойства бесконечно малых величин:
Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая;
Произведение бесконечно малой величины на ограниченную функцию есть величина бесконечно малая;
Частное от деления бесконечно малой на функцию, предел которой отличен от нуля, есть величина бесконечно мала.
18. Бесконечно-большие функции и их свойства.
Функция
называется бесконечно
большой
при
(или
,
или
)
если для сколь угодно большого
положительного числа
найдется такое положительное число
(
),
что для всех
будет верно неравенство
.
При
(
)
функция
называется бесконечно
большой,
если для сколь угодно большого
положительного числа
найдется такое положительное число
,
что для всех
будет верно неравенство
.
Предел
бесконечно
большой
величины
в точке сгущения (или на бесконечности)
равен бесконечности, т.е.
.
Свойства бесконечно больших величин:
Произведение бесконечно большой величины на функцию, предел которой отличен от нуля, есть величина бесконечно большая;
Сумма бесконечно большой величины и ограниченной функции есть величина бесконечно большая;
Частное от деления бесконечно большой величины на функцию, имеющую предел в точке есть величина бесконечно большая.
Теорема.
Если
функция
есть бесконечно малая величина при
(
)
то функция
есть бесконечно большая величина при
(
).
Обратная
теорема.
Если
функция
есть бесконечно большая величина при
(
)
то функция
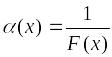есть бесконечно малая величина при
(
).
Сравнение бесконечно малых величин:
Две бесконечно малые величины
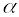и
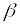называются бесконечно малыми одного
порядка, если предел их отношения есть
конечное число, отличное от нуля, т.е.
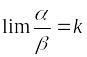
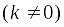;Величина называется бесконечно малой величиной высшего порядка по сравнению с , если предел отношения к равен нулю, т.е.
;Величина называется бесконечно малой величиной низшего порядка по сравнению с , если предел отношения к является бесконечно большой величиной, т.е.
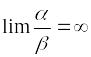;Две бесконечно малые величины и называются эквивалентными бесконечно малыми, если предел их отношения равен единице, т.е.
