12.Смешанное произведение векторов.

Смешанным произведением тройки векторов , и называется число, равное скалярному произведению вектора на векторное произведение 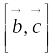. Если рассматриваемые векторы , и некомпланарны, то векторное произведение есть вектор, длина которого численно равна площади построенного на них параллелограмма. Направлен этот вектор по нормали к плоскости параллелограмма. Если этот вектор скалярно умножить на вектор , то получившееся число будет равно произведению площади основания параллелепипеда, построенного на тройке векторов , и , и его высоты, т.е. объему этого параллелепипеда.

Таким образом, смешанное произведение векторов 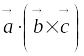(которое обозначается 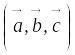) есть число, абсолютная величина которого выражает объем параллелепипеда, построенного на векторах , и .

Знак произведение положителен, если векторы , и , образуют правую тройку векторов, т.е. вектор направлен так, что кратчайший поворот от к виден из его конца совершающимся против часовой стрелки.

Из геометрического смысла смешанного произведения непосредственно следует необходимое и достаточное условие некомпланарности векторов , и : для того, чтобы векторы , и были некомпланарными необходимо и достаточно, чтобы их смешанное произведение было отлично от нуля.

Если , и , то:

,

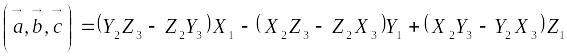или в свернутой форме:

.

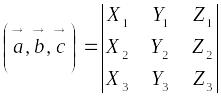Справедливы следующие свойства смешанного произведения векторов:

1. Смешанное произведение не меняется при циклической перестановке его сомножителей ;

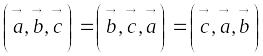2. При перестановке двух соседних множителей смешанное произведение меняет свой знак на противоположный .

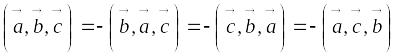13.Функция. Основные понятия.

Пусть ‑ некоторое числовое множество и пусть задан закон (правило) , по которому каждому числу ставится в соответствие единственное число , обозначаемое . Тогда говорят, что на множестве задана функция и записывают: или Чаще используют более простую терминологию: задана функция , .

Множество называют областью определения функции . Множество называют множеством значений функции . При этом называют независимой переменной или аргументом функции, – зависимой переменной или значением функции, а – характеристикой функции. Для обозначения функциональной зависимости можно употреблять любую другую букву ( , , , и т.д.). Частное значение функции при записывается как .

Существуют аналитический, графический, табличный и др. способы задания функции.

При аналитическом способе зависимость между переменными определяется формулами. Если при этом множество не указано, то считают, что функция задана в естественной области определения, т.е. на таком множестве, где эти формулы имеют смысл.

При графическом способе задания функции зависимость между переменными отражается с помощью графика. Графиком функции на плоскости называется геометрическое место точек , координаты которых связаны функциональной зависимостью.

При табличном способе задания функции выписываются в определенном порядке значения аргумента и соответствующие значения функции. Таблица дает не все значения функции, причем промежуточные значения функции могут быть найдены лишь приближенно при решении интерполяционной задачи. Поэтому в общем случае найти точное аналитическое выражение функции по ее табличным данным нельзя. Однако всегда можно построить интерполяционную формулу, и притом не одну (например, многочлен Лагранжа), которая для значений аргумента, имеющихся в таблице, будет давать соответствующие табличные значения функции.

Функции характеризуются рядом свойств, к важнейшим из которых относятся: четность, нули, периодичность, ограниченность, монотонность функции, а также наличие у функции асимптот и обратной функции:

• Функция называется четной, если для любого значения ее аргумента из области определения выполняется равенство 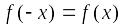. Сумма, разность и произведение четных функций есть функция четная;

• Функция называется нечетной, если для любого значения аргумента из области ее определения выполняется равенство 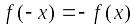. Сумма и разность нечетных функций есть функция нечетная, а частное и произведение нечетных функций – функция четная;

• Нулями функции называют значения аргумента, при которых функция обращается в ноль. Графически нулями функции являются точки пересечения графика функции с осью абсцисс;

• Функция называется периодической, если существует числ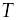о такое, что для каждого значения аргумента из области ее определения выполняется равенство . Число называют периодом этой функции;

• Функция называется возрастающей на некотором промежутке, если для любых значений из этого промежутка, большему значению аргумента соответствует большее зна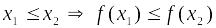чение функции, т.е. . Функция называется убывающей на некотором промежутке, если для любых значений из этого промежутка, большему значению аргумента соответствует меньшее значение функции, т.е. . Как возрастающие, так и убывающие функции называются монотонными;

• Асимптотой графика функции называется прямая, к которой сколь угодно близко приближается график данной функции при стремлении аргумента к бесконечности (горизонтальная и наклонная асимптоты), или к некоторому числу 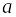(вертикальная асимптота);

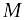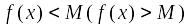• Функция называется ограниченной сверху (снизу), если существует число такое, что для каждого значения аргумента из области ее определения . Функция называется ограниченной, если существует число 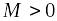такое, что для каждого значения аргумента из области ее определения ;

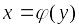• Функция называется обратной по отношению к , если при подстановке её вместо аргумента получается тождественное равенство: ;

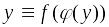• Если каждому значению переменной соответствует одно значение переменной , то 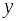называется однозначной функцией от ; если хотя бы некоторым значениям переменной соответствует несколько (два, три или бесконечное множество) значений , то называется многозначной (двузначной, трехзначной и т.д.) функцией от .