37. Необходимость введения и понятие ско случайных величин. Теорема о ско суммы взаимно независимых случайных величин (словесная формулировка, мат.Запись, доказательство).

Для оценки рассеяния возможных значений слу­чайной величины вокруг ее среднего значения кроме дис­персии служат и некоторые другие характеристики. К их числу относится среднее квадратическое отклонение.Средним квадратическим отклонением св Х называют квадратный корень из дисперсии: Легко показать, что дисперсия имеет размерность, равную квадрату размерности св. Так как среднее квадратическое отклонение равно квадратному

с размерностью X. Поэтому в тех случаях, когда жела­тельно, чтобы оценка рассеяния имела размерность слу­чайной величины, вычисляют среднее квадратическое от­клонение, а не дисперсию. Например, если Х выражается

Пример. Случайная величина Х задана законом распределения

Искомое среднее квадратическое отклонение

Среднее квадратическое отклонение суммы взаимно независимых св. Теорема. Среднее квадратическое отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин: Доказательство. Обозначим через Х сумму рас­сматриваемых взаимно независимых величин: Дисперсия суммы нескольких взаимно независимых св равна сумме дисперсий слагаемых поэтому

Отсюда или окончательно

37. Понятие момента: к-го порядка, начального, абсолютного, центрального – их математическая запись. С какими моментами и какого порядка связаны понятия математического ожидания и дисперсии случайной величины. Формулы вычисления центральных моментов 2-го, 3-го и 4-го порядков через начальные моменты.

мож М(Х) и дисперсия D(Х) являются част­ными случаями более общего понятия, называемого моментом рас­пределения случайной величины.. Моментом распределения k-го порядка случайной величины X относи­тельно некоторой постоянной С называется математическое ожидание k-й степени отклонения X oт постоянной С: M(X – C)^k

Если постоянная С = 0, то момент называется начальным и обозначается: Начальный момент k-го порядка абсолютной величины называется абсолютным моментом: Если в качестве С берется математическое ожидание т_х случайной величины X, т.е. центр ее распределения, то момент называется цент­ральным: При к = 1 имеем: , т.е. начальный момент первого порядка есть не что иное, как мож св; = М(Х-т_х) = 0 — центральный момент первого порядка, равен нулю.При к = 2: начальный момент второго порядка ν₂ = М(Х²) — мож квадрата св X; μ₂ = М(Х— т_х)² = D(X) — центр. момент 2 порядка есть дисперсия случайной величины X.. Центральные моменты целесообразно вычислять, используя формулы, выражающие центральные моменты через начальные:

39.Понятие коэффициента ассиметрии случайной величины, формула его вычисления. Примеры многоугольников распределения дискретных случайных величин, поясняющие влияние знака центрального момента 3-го порядка и коэффициента ассиметрии на их симметричность. Необходимые пояснения к этим многоугольникам.

Отношение центрального момента третьего порядка μ₃ к кубу среднеквадратичного отклонения называют коэффициентом асиммет­рии закона распределения вероятностей св: Коэффициент асимметрии является мерой симметричности ряда распределения относительно математического ожидания. приведены графики многоугольников распределения дсв.Для случайной величины X, математическое ожидание будет рав­но т_х = 4. Из графика закона распределения что он симметричен относительно математического ожидания. Если для данного закона распределения вероятности посчитать μ₃ и ко­эффициент асимметрии a, то увидим, что μ₃ = 0, а = 0. То есть при график закона распределения является симметричным относительно математического ожидания т_х .

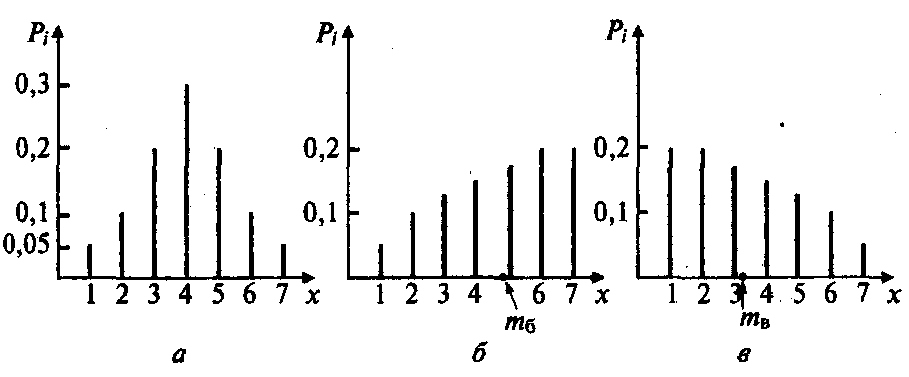
Из приведенных графиков на Рис. 1 б и 1 в видно, что закон распределения вероят­ностей для этих случайных величин является несимметричным отно­сительно математического ожидания.Для закона распределения вероятностей, приведенного на рис. 1, в, центральный момент третьего порядка μ₃ и коэффициент асимметрии будут иметь отрицательные значения. Для закона распределения вероятностей, приведенного на рис. 1, б, центральный момент третьего порядка и коэффициент асимметрии бу­дут иметь положительные значения.

37. Сущность и значение для практики теоремы Чебышева для достаточно большого числа независимых случайных величин. Основное неравенство данной теоремы и пояснения к нему. Пример(ы) применения данной теоремы из жизнедеятельности человечества.

Сущность доказанной теоремы такова: хотя от­дельные независимые случайные величины могут прини­мать значения, далекие от своих математических ожиданий, среднее арифметическое достаточно большого числа случай­ных величин с большой вероятностью принимает значе­ния, близкие к определенному постоянному числу, а именно в частном случае). Иными словами, отдельные случайные величины могут иметь значительный разброс, а их среднее арифметическое рассеянно мало.Итак, среднее арифметическое достаточно большого числа независимых случайных величин (дисперсии которых равномерно ограничены) утрачивает характер случайной величины. Объясняется это тем, что отклонения каждой из величин от своих математических ожиданий могут быть как положительными, так и отрицательными, а в среднем арифметическом они взаимно погашаются. Теорема Чебышева справедлива не только для дискрет­ных, но и для непрерывных случайных величин; Значение теоремы Чебышева для практики. Приведем примеры применения теоремы Чебышева к решению практических задач.Обычно для измерения некоторой физической величины производят несколько измерений и их среднее арифме­тическое принимают в качестве искомого размера. При каких условиях этот способ измерения можно считать правильным? Ответ на этот вопрос дает теорема Чебы­шева (ее частный случай).Действительно, рассмотрим результаты каждого измерения как случайные величины X_1, X_1, …. X_n. К этим величинам можно применить теорему Чебышева, если: 1) они попарно независимы, 2) имеют одно и то же ма­тематическое ожидание, 3) дисперсии их равномерно огра­ничены. Первое требование выполняется, если результат каж­дого измерения не зависит от результатов остальных. Второе требование выполняется, если измерения произ­ведены без систематических (одного знака) ошибок. В этом случае математические ожидания всех случайных величин одинаковы и равны истинному размеру а. Третье требо­вание выполняется, если прибор обеспечивает определен­ную точность измерений. Хотя при этом результаты отдельных измерений различны, но рассеяние их огра­ничено. Если все указанные требования выполнены, мы вправе применить к результатам измерений теорему Чебышева: при достаточно большом п вероятность неравенства как угодно близка к единице. Другими словами, при достаточно большом числе измерений почти достоверно, что их среднее арифметическое как угодно мало отли­чается от истинного значения измеряемой величины.Итак, теорема Чебышева указывает условия, при ко­торых описанный способ измерения может быть приме­нен. Однако ошибочно думать, что, увеличивая число измерений, можно достичь сколь угодно большой точ­ности. Дело в том, что сам прибор дает показания лишь с точностью ⁺_- α ; поэтому каждый из результатов изме­рений, а следовательно, и их среднее арифметическое будут получены лишь с точностью, не превышающей точности прибора.На теореме Чебышева основан широко применяемый в статистике выборочный метод, ( по сравнительно небольшой случайной выборке судят о всей совокупности исследуемых объектов). Для практики теорема Чебышева имеет неоценимое зна­чение.

37. Функция распределения случайной величины: необходимость её введения, определение; математическая запись; геометрическое толкование её понятия, второе название этой функции и её причина. Точное понятие непрерывной случайной величины.

Вспомним, что дискретная случайная величина может быть задана перечнем всех ее возможных значений и их вероятностей.Такой способ задания не является общим: он неприменим, например, для непрерывных случайных величин.

Действительно, рассмотрим случайную величину X, возможные значения которой сплошь заполняют интервал (а,b). Можно ли составить перечень всех возможных значений X? Этот пример указывает на целесообразность дать общий спо­соб задания любых св. С этой целью и вводят понятие функции распределения вероятностей случайной величины.

Пусть х — действительное число. Вероятность события, состоящего в том. что Х примет значение, меньшее х. т. е.

Функцией распределения называют функцию F (х), опре­деляющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х, т. е.

Геометрически это равенство можно истолковать так: F (х) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х. «функция распределения= «интегральная функция». Теперь можно дать более точное определение непре­рывной св: св назы­вают непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с не­прерывной производной.

37. Первое и второе свойства функции распределения случайной величины – словесная формулировка, математическая запись, доказательство, 2 следствия для второго свойства и их доказательство. Способы задания функции распределения.

Свойство 1. Значения функции распределения принадлежат отрезку [a, b]: Доказательство. Свойство вытекает из опреде­ления функции распределения как вероятности: вероят­ность всегда есть неотрицательное число, не превышающее единицы. Свойство 2. F (х) —неубывающая функция, т. е.

По теореме сложения имеем

О тсюда

и ли

Так как любая вероятность есть число неотрицательное, точто и требовалось доказать.

Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале (а, b), равна приращению функции распределения на этом ин­тервале:

Это важное следствие вытекает из формулы (*), если

Пример. Случайная величина Х задана функцией распределения

Найти вероятность того, что в результате испытания Х примет зна­чение. принадлежащее интервалу (0. 2): Решение. Так как на интервале (0, 2), по условию,

то Итак,

Следствие 2. Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю.

Используя это положение, легко убедиться в справедли­вости равенств

Таким образом, имеет смысл рас­сматривать вероятность попадания ее в интервал, пусть даже сколь угодно малый. Например, инте­ресуются вероятностью того, что размеры деталей не выходят за дозволенные границы, но не ставят вопроса о вероятности их совпадения с проектным размером.

Заметим, что было бы неправильным думать, что равенство нулю вероятности означает, что событие невозможно (если, конечно, не ограничиваться классическим определением вероятности). Действительно, в результате испытания случайная величина обязательно примет одно из возможных значений, в частности, это значение может оказаться равным .

37. Третье свойство функции распределения случайной величины: словесная формулировка, математическая запись, следствие и его доказательство. График функции распределения для дискретной, непрерывной и кусочно-непрерывной случайных функций, его основные свойства.

Свойство 3. Если возможные значения случайной величины «x» принадлежат интервалу , то: 1) при ; 2) при .

довательно, вероятность его равна единице.

Следствие. Если возможные значения непрерывной случайной величины расположены на всей оси «х», то спра­ведливы следующие предельные соотношения: График функции распределения

График расположен в полосе, ограниченной прямыми у=0, у=1 (первое свойство).При возрастании «x» в интервале (a, b), в котором заключены все возможные значения случайной величины, график «подымается вверх» (второе свойство). График функции распределения непрерывной случай­ной величины изображен на рис 1.

При ординаты графика равны нулю; при

ординаты графика равны единице (третье свойство). Замечание. График функции распределения дискретной слу­чайной величины имеет ступенчатый вид. Убедимся в этом на примере. Пример. Дискретная случайная величина Х задана таблицей распределения Найти функцию распределения и начертить ее график.

верно, следовательно, его вероятность равна единице. Итак, функция распределения аналитически может быть запи­сана так: График этой функции приведен на рис. 3.

Функция распределения может быть задана в табличном, графическом или аналитическом виде.

В соответствии с определением функции распределения ,а также 3-го свойства функции распределения, а именно, «если возможные значения случайной величины «x» принадлежат интервалу , то при », то для дискретной случайной величины Х можно записать: (****)

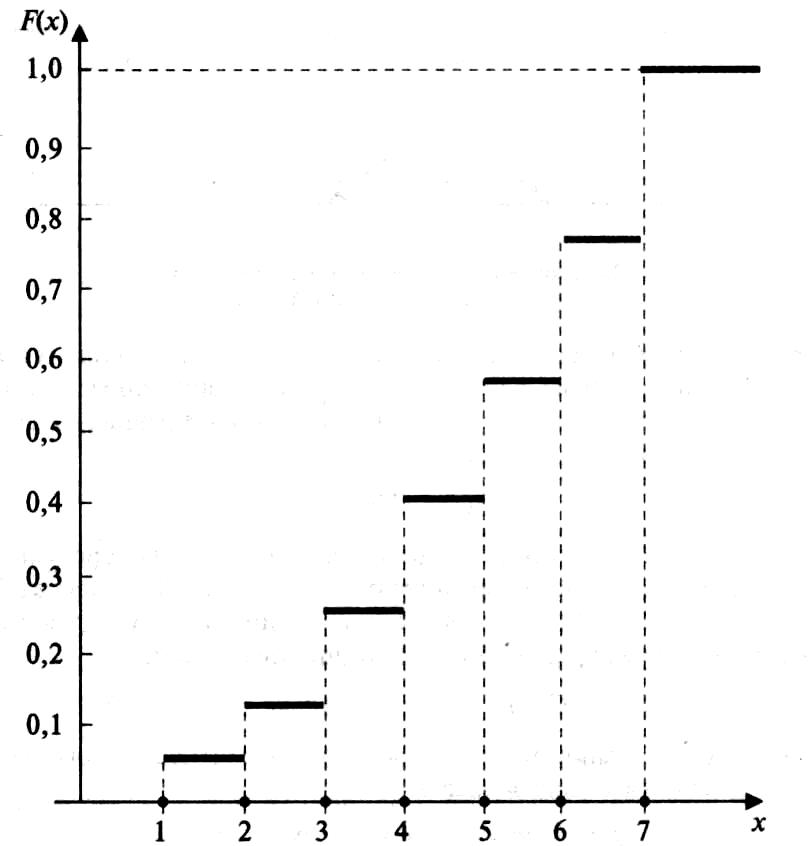
Пример.Закон распределения случайной величины Х в табличной форме

	1	2	3	4	5	6	7
	0,053	0,083	0,113	0,143	0,173	0,203	0,23

Представить функцию распределения дсв Х в табличной и графической форме представления.

Решение. Подставляя в формулу (****) значения вероятностей из таблицы 3.1 получим для всех возможных значений случайной величины Х значения функции распределения , которые оформим в виде таблицы 3.2.

Табличная форма функции распределения дискретной случайной величины Х

	1	2	3	4	5	6	7
	0,053	0,136	0,249	0,392	0,565	0,768	1

Графическая форма представления функции распределения дискретной случайной величины Х, на основании результатов, представленных в таблице 3.2, изображена на Рис. 4.

В конечном итоге при текущих значениях х>7 получили, что функ­ция распределения будет равна:F(X) = Р(Х> 7) = Р₁+Р₂+Р₃ +Р₄ + Р₅ +Р₆+Р₇ = 1. (рисунок ступеньками - выше)