Вопрос66666666666666666666666666666666666666666666666666666

Разделив уравнение МДС (1.21) на число витков w1, получим

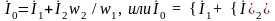(1.23)

где 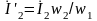, — ток нагрузки (вторичный ток), приведенный к числу витков первичной обмотки.

Другими словами, это такой ток, который в обмотке с числом витков w₁ создает такую же МДС, что и ток I₂ во вторичной обмотке w₂, т. е.

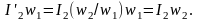
Преобразовав выражение (1.23), получим уравнение токов трансформатора:

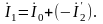(1.24)

Из этого уравнения следует, что первичный ток I₁ можно рассматривать как сумму двух составляющих: составляющую I₀, создающую МДС I₀w₁, необходимую для наведения в магнитопроводе основного магнитного потока Ф, и составляющую – I’₂, которая, создавая МДС – I’₂ w₁ компенсирует МДС вторичной обмотки I₂w₂ трансформатора. Такое действие составляющих первичного тока приводит к тому, что любое изменение тока нагрузки I₂ сопровождается изменением первичного тока I₁ за счет изменения его составляющей – I’₂, находящейся в противофазе с током нагрузки I₂.

§ 1.6. Приведение параметров вторичной обмотки и схема замещения приведенного трансформатора

В общем случае параметры первичной обмотки трансформатора отличаются от параметров вторичной обмотки. Эта разница наиболее ощутима при больших коэффициентах трансформации, что затрудняет расчеты и построение векторных диаграмм, так как в этом случае векторы электрических величин первичной обмотки значительно отличаются по своей длине от одноименных векторов вторичной обмотки. Указанные затруднения устраняются приведением всех параметров трансформатора к одинаковому числу витков, обычно к числу витков первичной обмотки w₁. С этой целью все величины, характеризующие вторичную цепь трансформатора, — ЭДС, напряжение, ток и сопротивления — пересчитывают на число витков w₁ первичной обмотки.

Таким образом, вместо реального трансформатора с коэффициентом трансформации k = w₁/w₂ получают эквивалентный трансформатор с k=w₁/w’₂=1, где w’₂=w₁. Такой трансформатор называют приведенным. Однако приведение вторичных параметров трансформатора не должно отразиться на его энергетических показателях: все мощности и фазовые сдвиги во вторичной обмотке приведенного трансформатора должны остаться такими, как и в реальном трансформаторе.

Так, электромагнитная мощность вторичной обмотки реального трансформатора Е₂I₂ должна быть равна электромагнитной мощности вторичной обмотки приведенного трансформатора:

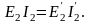(1.27)

Подставив значение приведенного тока вторичной обмотки I₂ = I₂(w₂/w₁,) в (1.27), получим формулу приведенной вторичной ЭДС:

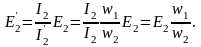(1.28)

Так как U₂I₂ ≈U’₂I’₂, то приведенное напряжение вторичной обмотки

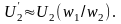(1.29)

Из условия равенства потерь в активном сопротивлении вторичной обмотки имеем 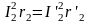. Определим приведенное активное сопротивление:

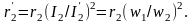(1.30)

Приведенное индуктивное сопротивление рассеяния вторичной обмотки определяют из условия равенства реактивных мощностей 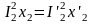, откуда

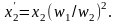(1.31)

Приведенное полное сопротивление вторичной обмотки трансформатора

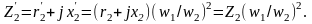(1.32)

Приведенное полное сопротивление нагрузки, подключенной на выводы вторичной обмотки, определим по аналогии с (1.32):

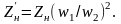(1.33)

Уравнения напряжений и токов для приведенного трансформатора имеют вид

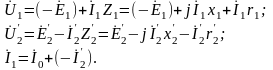(1.34)

Эти уравнения устанавливают аналитическую связь между параметрами трансформатора во всем диапазоне нагрузок от режима х.х. до номинальной.

Еще одним средством, облегчающим исследование электромагнитных процессов и расчет трансформаторов, является применение электрической схемы замещения приведенного трансформатора. На рис. 1.18, а представлена эквивалентная схема приведенного трансформатора, на которой сопротивления r и х условно вынесены из соответствующих обмоток и включены последовательно им. Как было установлено ранее, в приведенном трансформаторе k = 1, а поэтому 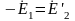. В результате точки А и а, а также точки X и х на схеме имеют одинаковые потенциалы, что позволяет электрически соединить указанные точки, получив Т–образную схему замещения приведенного трансформатора (рис. 1.18, б). В электрической схеме замещения трансформатора магнитная связь между цепями заменена электрической.

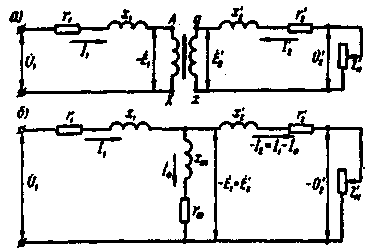
Рис. 1.18. Эквивалентная схема (в) и схема замещения (б) приведенного

Схема замещения приведенного трансформатора удовлетворяет всем уравнениям ЭДС и токов приведенного трансформатора (1.34) и представляет собой совокупность трех ветвей: первичной — сопротивлением Z₁ = r₁ + jx₁ и током 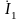; намагничивающей — сопротивлением Z_m=r_m+jx_m и током 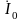; вторичной — с двумя сопротивлениями: сопротивлением собственно вторичной ветви Z'₂ = r’₂ + jx'₂ и сопротивлением нагрузки Z'_H = r_н' ± jx'_H и током . 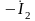Изменением сопротивления нагрузки Z'_H на схеме замещения могут быть воспроизведены все режимы работы трансформатора.

Параметры ветви намагничивания Z_m = r_m + jx_m определяются током х.х. Наличие в этой ветви активной составляющей r_m обусловлено магнитными потерями в трансформаторе (см. § 1.14).

Все параметры схемы замещения, за исключением Z'_H, являются постоянными для данного трансформатора и могут быть определены из опыта х.х. и опыта к.з. (см. §1.11).