6. Системы линейных дифференциальных уравнении с постоянными коэффициентами

Решить систему ,

где x(t),y(t),z(t)-неизвестные функции, a -их производные по аргументу t.

Решение. Исключим x , y из этих уравнений. Для этого из треть­его уравнения найдём . Продифференцируем полученное равен­ство по t: , подставив значения x и в первое уравнение, найдем из него , следовательно, . Подставив значения у , , x во второе уравнение, будем иметь или Получим линейное однородное дифференциальное уравнение третьего порядка. Составим характеристическое уравнение:

Следовательно, Чтобы определить неизвестные функции x(t) и y(t), найдем и из последнего равенства:

откуда

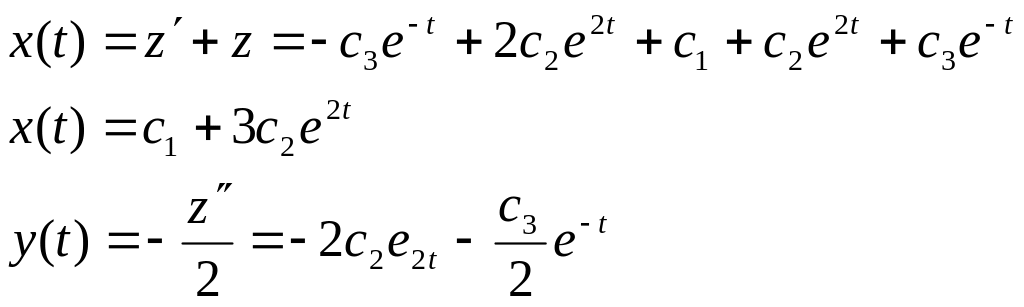
Общим решением данной системы будет система функции

6.I. Теоретические вопросы

1. Что называется дифференциальным уравнением первого порядка?

2. Что называется общим решением дифференциального уравнения первого порядка? 3.Дать определение частного решения. В чем состоит начальное условие для уравнения первого порядка?

3. Сформулировать теорему существования и единственности решения уравнения первого порядка.

4. Всякому ли начальному условию будет соответствовать частное решение уравнения?

5. Может ли быть так, что начальному условию соответствует не одно, а несколько частных решений?

6. Всякое ли значение можно приписать неопределенной постоянной в общем интеграле дифференциального уравнения?

7. Может ли различным начальным условиям соответствовать одно и то же решение?

8. Может ли дифференциальное уравнение не иметь ни одного решения?

9. Дать геометрическую иллюстрацию частного и общего решений диф­ференциального уравнения первого порядка.

10. Дать определение дифференциального уравнения с разделявшимися переменными к указать метод его интегрирования.

11. Дать определение дифференциального уравнения первого порядка и указать метод его интегрирования.

12. Какое уравнение первого порядка называется линейным? Изложить способ его решения.

13. Какое уравнение первого порядка называется уравнением Бернулли? Изложить способ его решения.

14. Какое уравнение первого порядка называется уравнением в полных дифференциалах? Описать способы его решения.

15. Поле направлении, определяемое уравнением 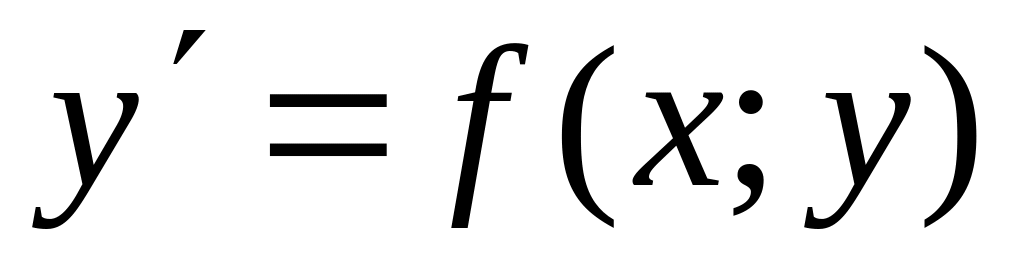. Изоклины, Метод Эйлера численного интегрирования дифференциального урав­нения первого порядка.

16. Какие точки являются особыми для дифференциального уравнения первого порядка? Примеры.

17. Что называется дифференциальным уравнением второго n-го поряд­ка? Сформулировать теорема Коши для дифференциального уравнения второго и n-го порядка.

18. Интегрирование дифференциальных уравнений вида 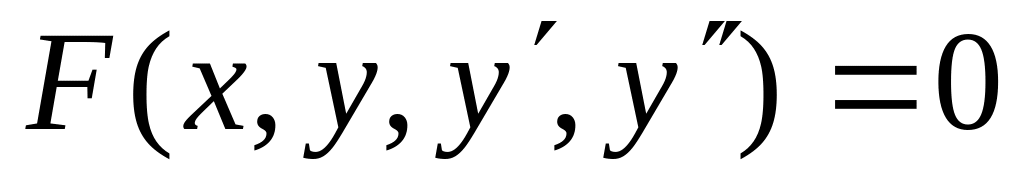путем понижения порядка.

19. Что называется линейным дифференциальным уравнением второго порядка? n-го порядка?

20. Является ли уравнение 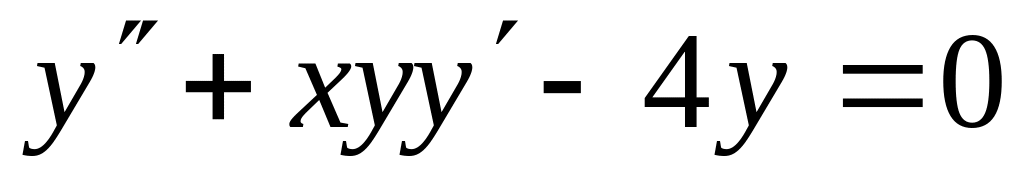линейным, если нет, то почему?

21. Являются ли функция 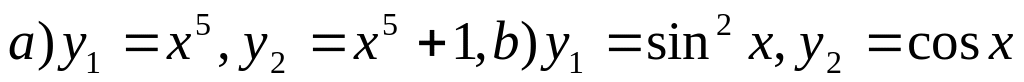линейно независимыми на всей числовой оси?

22. Приведите пример двух линейно зависимых функций на отрезке (0.1).

23. Линейный оператор, его свойства. Свойства решений линейного, однородного дифференциального уравнения.

24. Какая система функций называется линейно независимой? Условие линейной независимости частных решении линейного, дифференциально­го уравнения n-го порядка. Определитель Вронского.

25. Сформулировать и доказать теорему о структуре общего решения линейного, однородного дифференциального уравнения.

26. Решение линейных, однородных уравнений с постоянными коэффициента­ми в случае: а) действительных различных корней характеристичес­кого уравнения; б) действительных кратных корней характеристичес­кого уравнения.

27. Сформулировать и доказать теорему о структуре общего решения линейного, неоднородного дифференциального уравнения.

28. Разъяснить правило отыскания частного решения уравнение с пра­вой частью вида .

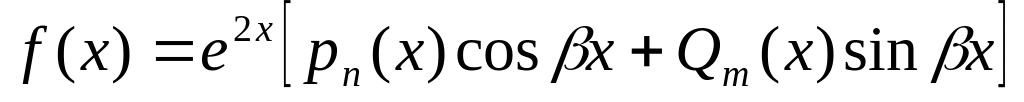29. Как можно находить решение уравнения с правой частью, если правая часть его представлена в виде суммы нескольких функции?

30. Метод вариации производных постоянных для линейного, неоднород­ного дифференциального уравнения с постоянными коэффициентами.

31. Что называется системой дифференциальных уравнений? Что называется решением такой системы?

32. Какая система дифференциальных уравнений называется нормальной?

33. Описать примеры сведения нормальной системы к одному уравнению высшего порядка.

34. Сформулировать свойства решений линейной системы дифференциальных уравнений.

6.2. Задачи, связанные с выводом какого-то дифференциаль­ного уравнения и его решением.

1. Составить уравнение кривой, преходящей через точку А(a, а) и обладающtй следующим свойством: если в любой точке М (x;y) кривой с ординатой pm провести касательную до пересечения с осью OY в точке Т, то площадь трапеции ОТМР есть величина постоянная, равная .

2. Найтн форму зеркала, собирающего все параллельные лучи в одну точку, предварительно построив чертеж.

3. Температура торфяного брикета, вышедшего из пресса, в течение 10 кинут понижается со 100° до 40°. Температура окружающего воздуха 20°. Через сколько минут от начала охлаждения температу­ра брикета понизится до 25°?

4. Найти кривые, у которых площадь трапеции, ограниченная осями координат -касательной и ординатой любой точки касания, есть величина постоянная, равная .

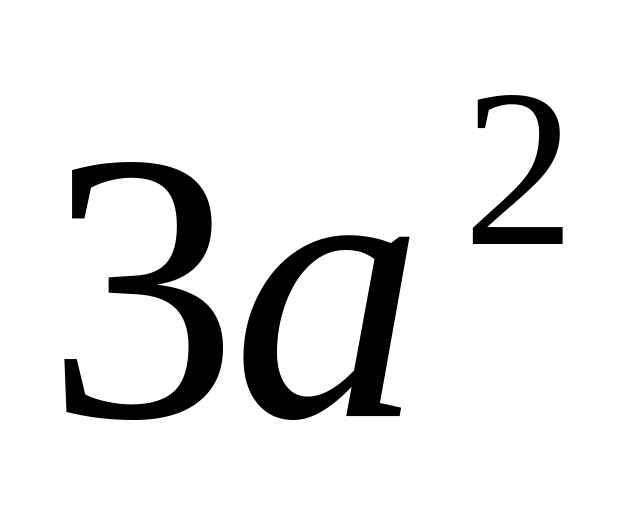5. Найти кривую, у которой точка пересечения любой касательной с осью абсцисс одинаково удалена от точки касания и от начала ко­ординат.

6. Найти кривые, у которых площадь треугольника, ограниченного касательной осью OX и отрезком от начала, координат до точки касания, есть величина постоянная, равная .

7. Найти кривую, у которой абсцисса центра тяжести плоской фигура, ограниченной осями координат этой кривой и ординатой любой точки, равна 3/4 абсциссы этой точки.

8. Найти кривую, проходящую через точку А(0,1), для которой треу­гольник, образованный осью OY, касательной к кривой в произ­вольной ее точке и радиусом--вектором точки касания - равнобед­ренный (причем основанием его служит отрезок касательной от точки до оси).

9. Найти кривую, у которой подкасательная в k раз больше абсциссы точки касания.

10. Найти кривую, у которой квадрат длины отрезка, отсекаемого каса­тельную от оси ординат, равен произведение координат точки касания.

11. Найти линию, у которой начальная ордината любой касательной на две единице масштаба меньше абсцисса точки касания.

12. Температура вынутого из печи хлеба в течение 20 мин. падает от 100° до 60°. Температура воздуха 25°. Через сколько времени от начала охлаждения температура хлеба понизится до 30°?

13. Определить время опорожнения заполненной керосином цистерны, имевшей длину l и диаметр d, через короткий сливной патрубок площади поперечного сечения u.

14. Материальная точка массой т движется прямолинейно под дейст­вием силы F, пропорциональной времени от начала движения и об­ратно пропорциональной скорости движения V. Установить зави­симость между скоростью и временам, если T=0,V=0.

15. Найти кривую, у которой отрезок касательной, заключенный меж­ду осями координат, делится пополам в точке касания.

16. Найти кривую, у которой нормаль в любой ее точке равна расстоянию этой точки от начала координат.

17. Найти кривую, зная, что площадь, заключенная между осями коор­динат этой кривой и ординатой любой точки на ней, равна кубу этой ординаты.

18. Найти линию, для которой абсцисса центра тяжести криволиней­ной трапеция, образованно образованной осями координат, прямой x=a и линией, была равна ¾ (при любой a).

19. Найти кривую, проходящую через точки (4;3), если угловой ко­эффициент касательной к кривой всегда в два раза меньше угло­вого коэффициента радиуса--вектора точки касания.

20. Найти уравнение кривой, у которой подкасательная равна сред­нему арифметическому координаты точки касания.

21. Найти линию, у которой начальная ордината любой касательной равна соответствующей поднормали.

22. Тело движется прямолинейно с ускорением, пропорциональным произведению скорости движения V на время t. Установить зависимость между V и t, если при t=0,V=V₀.

23. Найти кривую, для которой отрезок t=MT касательной от точ­ки касания М до точки пересечения Т с осью OY был бы посто­янным .

24. Поднормаль равна отрезку, отсекаемому касательной по оси OY. Кривая проходит через точку (1;1). Составить ее уравнение.

25. Найти уравнение кривой, у которой отрезок, отсекаемый касательной на оси ординат, равен поднормали.