Вопрос 12:

Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Единица измерения СИ: кг·м².

Обозначение: I или J.

Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек. Осевые моменты инерции некоторых тел.

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

,где:

• m_i — масса i-й точки,

• r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.

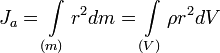,где:

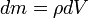•  — масса малого элемента объёма тела  ,

•  — плотность,

•  — расстояние от элемента   до оси a.

Если тело однородно, то есть его плотность всюду одинакова, то

Теорема Гюйгенса-Штейнера

Основная статья: Теорема Штейнера

Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласнотеореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

Если   — момент инерции тела относительно оси, проходящей через центр масс тела, то момент инерции относительно параллельной оси, расположенной на расстоянии   от неё, равен

,

где   — полная масса тела.

Например, момент инерции стержня относительно оси, проходящей через его конец, равен:

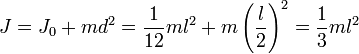
Вопрос 13:

Момент силы относительно точки. Момент силы относительно оси. Основной закон динамики вращательного движения.

В лекции тема «Кинетическая энергия вращательного тела».

Момент силы относительно точки:

Опр: M₀ = r*F (все это величины - векторы)

Направление: определяется по правилу Буравчика: если вращать Б. по направлению от r к F, то его поступательное движение укажет направление вектора момента силы.

(Далее идут всякие рисунки, гляньте их сами).

Модуль: M₀ = r*F*sin α, где r*sin α = h, а h – это плечо – расстояние от точки до линии действия силы.

Детали и уточнения:

1.Если h=o, то M=0 (Рисунок). Сила не создает вращательного момента относительно точки, если ее линия действия проходит через эту точку.

2.M = Fh – одинаков (Рисунок). Силу можно двигать вдоль линии ее действия, это не приводит к изменению ее вращающего момента.

Момент силы относительно оси – проекция вектора момента силы относительно любой точки, принадлежащей этой оси, на заданную ось.

Рисунок 1: M = F*r

Рисунок 2: Сила не создает вращательного момента относительно оси, если она параллельна этой оси.

Рисунок 3: Сила не создает вращательного момента, если ее линия действия пересекает ось вращения. M₀ = 0

Основной закон динамики вращательно движения:

1.Для поступательно движения:

ma = ∑F_i

2.Для вращательного движения:

I ε = ∑M