Вопрос1

1.Матрицы и линейные действия с ними. Свойства линейных операций с матрицами.

Матрицей размерности m x n называется прямоугольная таблица m x n чисел a ij , i=1,..., m, j=1,..., n:

расположенных в m строках и n столбцах. Матрица называется квадратной, если m=n (n - порядок матрицы).

Линейные матричные операции

По определению, чтобы умножить матрицу на число, нужно умножить на это число все элементы матрицы. Суммой двух матриц одинаковой размерности, называется матрица той же размерности, каждый элемент которой равен сумме соответствующих элементов слагаемых.

Сложение матриц.

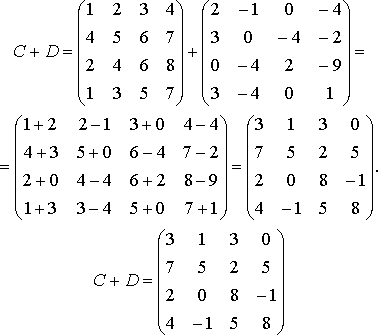
Вычитание Матриц.

Для того чтобы вычесть из матрицы А матрицу В. Следует матрицу В умножить на (-1), то есть умножить на (-1) каждый ее член, и сложить А+-В). Легко проверить, что операции сложения матриц и умножения матрицы на число, называемые линейными операциями, обладают следующими свойствами:

- свойство коммутативности;

- свойство ассоциативности;

- свойство дистрибутивности;

Здесь - матрицы, - числа, 0 - нулевая матрица.

2.Умножение матриц и его свойства.

Произведением матрицы A размеров m*n на матрицу B размеров n*k называется матрица C размеров m*k, элементы которой вычисляются по формуле

где i=1,...,m ,i=1,...,k.

Во-первых, в этом определении нужно обратить внимание на то, что важен порядок сомножителей, нужно знать, какой сомножитель первый, а какой -- второй.

Во-вторых, нужно отметить, что произведение определено только в том случае, если число столбцов первого сомножителя равно числу строк второго. Если это условие не выполняется, то произведение не определено.

В-третьих, размеры результата умножения определяются следующим образом: число строк результата равно числу строк первого сомножителя, а число столбцов результата равно числу столбцов второго сомножителя.

Правило вычисления элементов произведения можно сформулировать следующим образом: Для того, чтобы вычислить элемент произведения, стоящий в i -ой строке и j -ом столбце, нужно взять -ую строку первого сомножителя и j -ый столбец второго сомножителя, попарно перемножить их элементы, стоящие на одинаковых местах, и результаты сложить.

---------------------------------

------------------------------

, B·A – не имеет смысла.

Таким образом, эти простые примеры показывают, что матрицы, вообще говоря, не перестановочны друг с другом, т.е. A∙B ≠ B∙A.

Можно проверить, что умножение матриц подчиняется ассоциативному и дистрибутивному законам, т.е. (AB)C=A(BC) и (A+B)C=AC+BC.

Легко также проверить, что при умножении квадратной матрицы A на единичную матрицу E того же порядка вновь получим матрицу A, причём AE=EA=A.

Можно отметить следующий любопытный факт. Как известно произведение 2-х отличных от нуля чисел не равно 0. Для матриц это может не иметь места, т.е. произведение 2-х не нулевых матриц может оказаться равным нулевой матрице.

Св-ва матриц:

А+В=В+А; λ (А+В)=λА+λВ; (АВ)С=А(ВС); (А+В)С=АС+ВС; С(А+В)=СА+СВ; (А+В)n=Аn+Вn; (λ А)n= λ Аn; (АВ)n=ВnАn