
- •Постоянный электрический ток
- •1.Электрический ток и его характеристики. Подвижность носителей тока.
- •2. Электродвижущая сила источника тока.
- •3. Законы Ома для неоднородного и однородного участков цепи. Напряжение. Закон Ома для замкнутой цепи.
- •4. Сопротивление и проводимость. Зависимость удельного сопротивления металлов от температуры. Сверхпроводимость. Соединение проводников.
- •5. Разветвленные цепи. Правила Кирхгофа.
- •6. Работа и мощность электрического тока. Закон Джоуля-Ленца. Коэффициент полезного действия источника тока.
- •Природа носителей тока в металлах. Закон Ома и закон Джоуля-Ленца в дифферен-циальной форме.
- •Магнитное поле в вакууме
- •Магнитное поле. Опыты Эрстеда. Силовое действие магнитного поля. Взаимодействие токов. Магнитный момент контура с током. Индукция магнитного поля.
- •Закон Био-Савара-Лапласа. Поле движущегося заряда.
- •Магнитное поле прямого и кругового токов:
- •Закон Ампера. Взаимодействие параллельных токов.
- •5. Сила Лоренца. Движение заряженных частиц в магнитном поле. Линейная магнитная ловушка.
- •6.Движение заряженных частиц во взаимно перпендикулярных полях. Определение удельного заряда электрона. Циклотрон. Селектор скоростей. Масс-спектрометр.
- •Эффект Холла. Магнитогидродинамические генераторы.
- •Вихревой характер магнитного поля. Теорема Ампера о циркуляции индукции магнитного поля в дифференциаль-ной и интегральной форме для магнитных полей в вакууме.
- •Применение теоремы о циркуляции вектора в. Магнитное поле соленоида и тороида.
- •Работа перемещения проводника с током в магнитном поле.
- •12.Контур с током в однородном и неоднородном магнитном поле.
- •Магнитное поле в веществе
- •Вопрос 2
- •Вопрос 3
- •Вопрос 4
- •Вопрос 5
- •Вопрос 6
- •Электромагнитная индукция
- •1.Явление электромагнитной индукции. Классические опыты Фарадея. Закон Фарадея. Правило Ленца.
- •1. Явление электромагнитной индукции. Классические опыты Фарадея. Закон Фарадея. Правило Ленца.
- •2. Вывод закона электромагнитной индукции. Природа эдс электромагнитной индукции. Токи Фуко.
- •3. Явление самоиндукции. Зависимость эдс самоиндукции от скорости изменения силы тока в контуре.
- •4. Индуктивность. Индуктивность бесконечно длинного соленоида.
- •5. Взаимная индукция. Трансформаторы.
- •6. Энергия магнитного поля. Плотность энергии магнитного поля.
- •Вихревое электрическое поле. Бетатрон.
- •Ток смещения. Вихревое магнитное поле.
- •Уравнения Максвелла в интегральной и дифференциальной формах. Интегральная форма
- •Дифференциальная форма
- •Уравнения Максвелла для стационарных полей.
- •Электромагнитные колебания и волны
- •Волновая оптика
- •Полосы равной толщины
- •Кольца Ньютона
- •§ 185. Дисперсия света
- •§ 183. Разрешающая способность оптических приборов
- •§ 182. Дифракция на пространственной решетке. Формула Вульфа - Брэггов
- •§ 190. Естественный и поляризованный свет
- •§ 191. Поляризация света при отражении и преломлении на границе двух диэлектриков
- •§ 192. Двойное лучепреломление
- •§ 193. Поляризационные призмы и поляроиды
- •§ 195. Искусственная оптическая анизотропия
- •§ 196. Вращение плоскости поляризации
- •§ 185. Дисперсия света
- •§ 200. Формулы Рэлея - Джинса и Планка
- •§ 154. Фазовая скорость. Волновое уравнение
- •§ 155. Принцип суперпозиции. Групповая скорость
- •§ 187. Поглощение (абсорбция) света
- •Квантовая оптика
Уравнения Максвелла для стационарных полей.
Таким
образом, первое
и второе уравнения Максвелла для стационарных
вихревых полей приводятся
к дифференциальной форме в виде
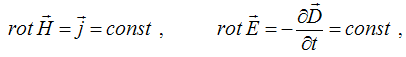 и
соответственно к интегральной форме в
виде
и
соответственно к интегральной форме в
виде
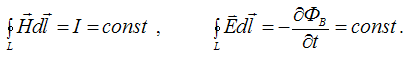
Электромагнитные колебания и волны
1.Колебательный контур — осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока (и напряжения)
Уравнение, описывающее свободные электрические колебания в контуре:
![]()
Ещё нужно возникновение в нем контура
2. Рассмотрим свободные затухающие колебания – колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшаются. Простейшим механизмом уменьшения энергии колебаний является ее превращение в теплоту вследствие трения в механических колебательных системах, а также омических потерь и излучения электромагнитной энергии в электрических колебательных системах.
Свободные
затухающие колебания в электрическом
колебательном контуре.
![]()
3. Характеристики затухающих колебаний.Чем меньше силы трения в системе, тем медленнее затухают колебания, тем лучше колебательная система. Для характеристики качества колебательной системы вводится ряд параметров: t = 1/b - время релаксации затухающих колебаний (за t амплитуда уменьшается в e раз).
![]() - логарифмический
декремент затухания;
N - число колебаний, в течение которых
амплитуда уменьшается в e раз.
Соответственно, exp(bT) - просто декремент
затухания.
- логарифмический
декремент затухания;
N - число колебаний, в течение которых
амплитуда уменьшается в e раз.
Соответственно, exp(bT) - просто декремент
затухания.
![]() - добротность
колебательной системы;
W(t) - энергия (полная) колебательной
системы в момент времени
- добротность
колебательной системы;
W(t) - энергия (полная) колебательной
системы в момент времени
4. Свободные незатухающие колебания-чётко не где не написано, там формулави выводят…
Формула
Томсона
выглядит следующим образом:![]()
5. Вынужденные электрические колебания — это периодические изменения силы тока в контуре и других электрических величин под действием переменной ЭДС от внешнего источника.
Это
уравнение вынужденных электрических
колебаний
![]()
Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса.
Обобщенное
гармоническое колебание в дифференциальном
виде:
![]()
Ещё нужно решение
Я лично не нашёл
6. Резонанс напряжений - резонанс, происходящий в последовательном колебательном контуре при его подключении к источнику напряжения, частота которого совпадает с собственной частотой контура.
Частота и амплитуда напряжения на конденсаторе при резонансе-долго и нудно искал но нечего нет…
Не всё полная херня, то что нужно нет…
7.Автоколеба́ния — незатухающие колебания в диссипативной динамической системе с нелинейной обратной связью, поддерживающиеся за счёт энергии постоянного, то есть непериодического внешнего воздействия.
Получение незатухающих колебаний:
Если конденсатор колебательного контура заряжен, то в контуре возникают затухающие колебания. Электрическая энергия WЭЛ переходит во внутреннюю энергию UВН.
![]()
Пополнять энергию колебательного контура можно, подзаряжая конденсатор. Для этого контур подключают к источнику тока. Контур подключается к источнику тока только в те интервалы времени, когда пластина конденсатора, присоединенная к положительному полюсу источника, заряжена положительно.
Если источник постоянного тока будет все время подключен к контуру, то в 1/2 Т энергия поступает в контур, а следующую 1/2 Т возвращается в источник, т. е. колебания затухают.
Незатухающие
колебания установятся в том случае,
если контур будет подключаться к
источнику только в первую половину
периода. Для выполнения такого условия
ключ должен замыкать и размыкать цепь
с частотой, соответствующей частоте
электромагнитных колебаний контура:
![]()
Однако механический ключ инертен.
Безынерционным ключом является транзистор. Транзистор обеспечивает поступление энергии к колебательному контуру, если напряжение на электронном переходе меняется синфазно с напряжением на контуре.
8.
Путём чисто
математических преобразований, без
каких-либо дополнительных предположений
эти уравнения
приводятся к виду: ![]()
![]()
А это есть ни что иное, как волновые уравнения для векторов напряженности электрического и магнитного полей. Мы знаем, что коэффициент в правой части уравнений есть обратный квадрат фазовой скорости волны; отсюда сразу находим эту скорость:
![]()
Общее
решение волнового уравнения:
![]()
Значение функции E (и H) для фиксированных значений координаты x и времени t является постоянным на плоскости, перпендикулярной к оси x. Поэтому такие волны E = E(x+vt ) и H =H(x +vt)называются плоскими.
9. Эне́ргия электромагни́тного по́ля — термин, под которым подразумевается энергия, заключенная в электромагнитном поле. Сюда же относятся частные случаи чистого электрического поля и чистого магнитного поля.
Для электромагнитной волны плотность потока энергии определяется вектором Пойнтинга S (в российской научной традиции — вектор Умова-Пойнтинга).
В
системе СИ вектор
Пойнтинга
равен:
![]()
— векторному произведению напряжённостей электрического и магнитного полей, и направлен перпендикулярно векторам E и H. Это естественным образом согласуется со свойством поперечности электромагнитных волн.
Вместе с тем, формула для плотности потока энергии может быть обобщена для случая стационарных электрических и магнитных полей, и имеет совершенно тот же вид:
Сам факт существования потоков энергии в постоянных электрических и магнитных полях, на первый взгляд, выглядит очень странно, но это не приводит к каким-либо парадоксам; более того, такие потоки обнаруживаются в эксперименте.
10. Электромагнитные волны — это поперечные волны (волны сдвига), в которых вектора напряжённостей электрического и магнитного полей колеблются перпендикулярно направлению распространения волны.
Электромагни́тное излуче́ние (электромагнитные волны) — распространяющееся в пространстве возмущение (изменение состояния) электромагнитного поля (то есть, взаимодействующих друг с другом электрического и магнитного полей).
Дипольное излучение (излучение в волновой зоне)
Приведённые формулы существенно упрощаются, если размеры системы много меньше длины излучаемой волны, то есть скорости зарядов много меньше c, а поле рассматривается на расстояниях много больших, чем длина волны. Такую область поля называют волновой зоной. Распространяющуюся волну можно в этой области считать практически плоской. Из всех членов в выражениях для и существенными оказываются только члены, содержащие вторые производные от так как
![]()
![]()
Выражения
для полей принимают вид ![]()
![]()
В
плоской волне интенсивность излучения
в телесный угол равна ![]()
поэтому
для дипольного излучения
![]()
где
— угол между векторами и Найдём полную
излучаемую энергию. Учитывая, что
проинтегрируем выражение по от до
Полное излучение равно
![]()
Работы Герца_-просто скопировал т.к. не чего нормального нет.
В 1887 году Г. Герцем впервые экспериментально получены электромагнитные волны. В его опытах ускоренное движение электрических зарядов возбуждались в двух металлических стержнях с шарами на концах (вибратор Герца). Колебания электрических зарядов в вибраторе создают электромагнитную волну. Только колебания в вибраторе совершает не одна заряженная частица, а огромное число электронов, движущихся согласовано. В электромагнитной волне векторы Е и В перпендикулярны друг другу. Вектор Е лежит в плоскости, проходящей через вибратор, а вектор В перпендикулярен этой плоскости. Излучение волн происходит с максимальной интенсивностью в направлении, перпендикулярном оси вибратора. Вдоль оси излучения не происходят. В обычном колебательном контуре (его можно назвать закрытым), почти всё магнитное поле сосредоточено внутри катушки, а электрическое внутри конденсатора. Вдали от контура электромагнитного поля практически нет. Такой контур очень слабо излучает электромагнитные волны. Для получения электромагнитных волн Герц использовал простое устройство, называемое сейчас вибратором Герца. Это устройство представляет собой открытый колебательный контур.
В его опытах ускоренное движение электрических зарядов возбуждались в двух металлических стержнях с шарами на концах (вибратор Герца). Колебания электрических зарядов в вибраторе создают электромагнитную волну. Только колебания в вибраторе совершает не одна заряженная частица, а огромное число электронов, движущихся согласовано. В электромагнитной волне векторы Е и В перпендикулярны друг другу. Вектор Е лежит в плоскости, проходящей через вибратор, а вектор В перпендикулярен этой плоскости. Излучение волн происходит с максимальной интенсивностью в направлении, перпендикулярном оси вибратора. Вдоль оси излучения не происходят. В обычном колебательном контуре (его можно назвать закрытым), почти всё магнитное поле сосредоточено внутри катушки, а электрическое внутри конденсатора. Вдали от контура электромагнитного поля практически нет. Такой контур очень слабо излучает электромагнитные волны. Для получения электромагнитных волн Герц использовал простое устройство, называемое сейчас вибратором Герца. Это устройство представляет собой открытый колебательный контур. К открытому колебательному контуру можно перейти от закрытого, если постепенно раздвигать пластины конденсатора, уменьшая их площадь и одновременно уменьшая число витков в катушке. В конце концов, получится прямой провод. Это и есть открытый колебательный контур. Емкость и индуктивность вибратора Герца малы. Поэтому частота колебаний весьма велика. В опытах Герца длина волны составляла несколько десятков сантиметров. Вычислив собственную частоту электромагнитных колебаний вибратора, Герц смог определить скорость электромагнитной волны. Она оказалась приближенно равна скорости света. Что в результате явилось блестящим подтверждением предсказания Максвелла.
