
- •1 . Обратное включение четырехполюсников. Уравнения четырехполюсников при прямом и обратном включении.
- •2. Передаточные функции четырехполюсника.
- •3. Операционный усилитель с обратной связью. Вывод коэффициента усиления по напряжению Ku.
- •4. Четырехполюсники и их уравнения типа y, z, a. Связь между их параметрами.
- •5. Определение характеристических параметров симметричного четырехполюсника через сопротивления холостого хода и короткого замыкания.
- •6. Опытный способ определения a-параметров четырехполюсника.
- •7. Определение характеристических параметров несимметричного четырехполюсника через a-параметры.
- •8. Каскадное соединение четырехполюсников.
- •9. Уравнения четырехполюсника с гиперболическими функциями.
- •35. Переходные процессы при скачкообразном изменении емкости в цепи. Некорректные коммутации.
- •10. Вторичные параметры четырехполюсника.
- •11. Определение входного сопротивления четырехполюсника в режимах холостого хода и короткого замыкания при согласованной нагрузке, при произвольной нагрузке через первичные и вторичные параметры.
- •19. Полосовой фильтр и его характеристики.
- •12. Работа четырехполюсников с обратной связью.
- •13. Определение характеристических параметров симметричного четырехполюсника через a-параметры.
- •14. Типы электрических фильтров. Определение коэффициентов затухания и фазы, характеристического сопротивления zст(f) в функции частоты для низкочастотного фильтра.
- •15. Высокочастотные реактивные фильтры.
- •16. Низкочастотные реактивные фильтры.
- •17. Пассивные rc-фильтры. Коэффициенты передачи для низкочастотных и высокочастотных фильтров.
- •18. Активный низкочастотный rc-фильтр.
- •23. Включение электрической цепи на напряжение произвольной формы. Интеграл Дюамеля.
- •24. Возникновение переходных процессов и законы коммутации.
- •25. Операторный метод расчета переходных процессов. Рассмотреть включение цепи r-l на постоянное напряжение операторным методом.
- •Алгоритм расчета переходного процесса операторным методом.
- •26. Переходной, установившийся (принужденный) и свободный процессы. Классический метод расчета.
- •27. Алгоритм расчета переходного процесса классическим методом в цепи первого порядка на примере подключения r-c-цепи к источнику постоянного напряжения.
- •28. Алгоритм расчета переходного процесса классическим методом в цепи первого порядка на примере подключения r-l-цепи к источнику постоянного напряжения.
- •29. Законы Ома и Кирхгофа в операторной форме. Пояснить принципы составления операторных схем замещения.
- •3 6.Продолжение
- •30. Пути восстановления оригинала функции по известному ее операторному изображению.
- •31. Алгоритм расчета переходного процесса классическим методом в цепи первого порядка на примере подключения r-l-цепи к источнику синусоидального напряжения.
- •32. Алгоритм расчета переходного процесса классическим методом в цепи второго порядка на примере подключения r-l-c-цепи к источнику постоянного напряжения.
- •33. Законы Кирхгофа в операторной форме. Эквивалентные операторные схемы замещения.
- •36. Переходные процессы при скачкообразном изменении индуктивности в цепи. Некорректные коммутации. Первый обобщенный закон коммутации.
- •1. Обратное включение четырехполюсников. Уравнения четырехполюсников при прямом и обратном включении.
- •2. Передаточные функции четырехполюсника.
15. Высокочастотные реактивные фильтры.
Схема простейшего высокочастотного фильтра приведена на рис. 3,а.
![]()
Для данного фильтра коэффициенты четырехполюсника определяются выражениями
|
(9) |
|
(10) |
|
(11) |
Как и для рассмотренного выше случая, А – вещественная переменная. Поэтому на основании (9)
![]() .
.
Данному неравенству удовлетворяет диапазон изменения частот
|
(12) |
Характеристическое сопротивление фильтра
|
(13) |
изменяясь в пределах от нуля до с ростом частоты, остается вещественным. Это соответствует, как уже отмечалось, работе фильтра, нагруженного характеристическим сопротивлением, в резонансном режиме. Поскольку такое согласование фильтра с нагрузкой во всей полосе пропускания практически невозможно, реально фильтр работает с в ограниченном диапазоне частот.
Вне
области пропускания частот
![]() определяется
из уравнения
определяется
из уравнения
|
(14) |
при
![]() .
Плавное изменение коэффициента затухания
в соответствии с (14) показывает, что в
полосе задерживания фильтр не является
идеальным.
.
Плавное изменение коэффициента затухания
в соответствии с (14) показывает, что в
полосе задерживания фильтр не является
идеальным.
Качественный
вид зависимостей
и
![]() для
низкочастотного фильтра представлен
на рис. 4.
для
низкочастотного фильтра представлен
на рис. 4.
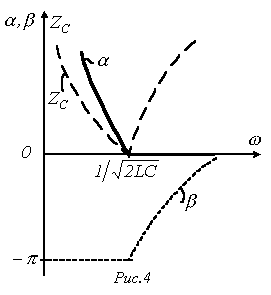
Следует отметить, что другим примером простейшего высокочастотного фильтра может служить П-образный четырехполюсник на рис. 3,б.
16. Низкочастотные реактивные фильтры.
Рассмотрим схему простейшего низкочастотного фильтра, представленную на рис. 1,а.
![]()
Связь коэффициентов четырехполюсника с параметрами элементов Т-образной схемы замещения определяется соотношениями (см. лекцию № 14)
![]()
или конкретно для фильтра на рис. 1,а
|
(2) |
|
(3) |
|
(4) |
Из уравнений четырехполюсника, записанных с использованием гиперболических функций (см. лекцию № 14), вытекает, что
![]() .
.
Однако
в соответствии с (2)
![]() -
вещественная переменная, а следовательно,
-
вещественная переменная, а следовательно,
|
(5) |
Поскольку
в полосе пропускания частот коэффициент
затухания
,
то на основании (5)
![]() .
.
Так
как пределы изменения
![]() :
:
![]() ,
- то границы полосы пропускания
определяются неравенством
,
- то границы полосы пропускания
определяются неравенством
![]() ,
,
которому удовлетворяют частоты, лежащие в диапазоне
|
(6) |
Для характеристического сопротивления фильтра на основании (3) и (4) имеем
|
(7) |
Анализ
соотношения (7) показывает, что с ростом
частоты w в пределах, определяемых
неравенством (6), характеристическое
сопротивление фильтра уменьшается до
нуля, оставаясь активным. Поскольку,
при нагрузке фильтра сопротивлением,
равным характеристическому, его входное
сопротивление также будет равно
![]() ,
то, вследствие вещественности
,
можно сделать заключение, что фильтр
работает в режиме резонанса, что было
отмечено ранее. При частотах, больших
,
то, вследствие вещественности
,
можно сделать заключение, что фильтр
работает в режиме резонанса, что было
отмечено ранее. При частотах, больших
![]() ,
как это следует из (7), характеристическое
сопротивление приобретает индуктивный
характер.
,
как это следует из (7), характеристическое
сопротивление приобретает индуктивный
характер.
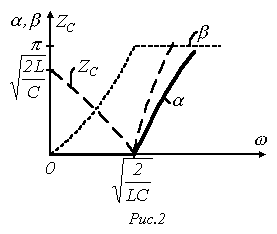
На рис. 2 приведены качественные зависимости и .
Следует
отметить, что вне полосы пропускания
![]() .
Действительно, поскольку коэффициент
А – вещественный, то всегда должно
удовлетворяться равенство
.
Действительно, поскольку коэффициент
А – вещественный, то всегда должно
удовлетворяться равенство
|
(8) |
Так
как вне полосы прозрачности
![]() ,
то соотношение (8) может выполняться
только при
,
то соотношение (8) может выполняться
только при
![]() .
.
В полосе задерживания коэффициент затухания определяется из уравнения (5) при . Существенным при этом является факт постепенного нарастания , т.е. в полосе затухания фильтр не является идеальным. Аналогичный вывод о неидеальности реального фильтра можно сделать и для полосы прозрачности, поскольку обеспечить практически согласованный режим работы фильтра во всей полосе прозрачности невозможно, а следовательно, в полосе пропускания коэффициент затухания будет отличен от нуля.
