6. Опытный способ определения a-параметров четырехполюсника.

Постоянные четырехполюсника можно найти из опытов холостого хода и короткого замыкания. Это особенно удобно, когда схема четырехполюсника неизвестна. Запишем основные уравнения четырехполюсника в A-параметрах.

Рассмотрим два предельных режима работы четырехполюсника 1. Прямой холостой ход. К первичным зажимам подведено напряжение, а вторичные зажимы разомкнуты . Уравнения четырехполюсника в этом случае примут вид.

2. Прямое короткое замыкание. К первичным зажимам подведено напряжение, а вторичные зажимы замкнуты накоротко . Уравнения четырехполюсника в этом случае примут вид. _{отсюда выражаем А-параметры. А=U1x/U2 ; C=I1x/U2 ; B=U1k/I2 ; D= I1k/I2.}

7. Определение характеристических параметров несимметричного четырехполюсника через a-параметры.

Входные сопротивления четырехполюсника Zвх1 и Zвх2, при которых наступает режим согласованного включения, называются собственными (характеристическими) сопротивлениями четырехполюсника и обозначаются Zс1 и Zс2. Выразим собственные сопротивления четырехполюсника через А-параметры. Для этого в выражениях (5.9) и (5.10) примем Zвх1 = Zг = Zс1 и Zвх2= Zн = Zс2 получим: Совместное решение этих уравнений относительно Zс1 и Zс2 дает следующие выражения: (5.15) (5.16) Для оценки собственных потерь энергии в четырехполюснике вводят в качестве меры, характеризующей, как передает четырехполюсник энергию (с потерями или без), понятие характеристическая (собственная) постоянная передачи четырехполюсника. В качестве такой характеристики используют логарифмическое отношение мощностей на входе S1 = U1I1 и выходе S2 = U2I2 четырехполюсника, которое записывается в виде следующего выражения: . Постоянная передача ЧП позволяет установить связь между входными и выходными параметрами, а именно токи и напряжения. Постоянная передачи ЧП выраженная через А-параметры имеет вид : g_c=ln( )

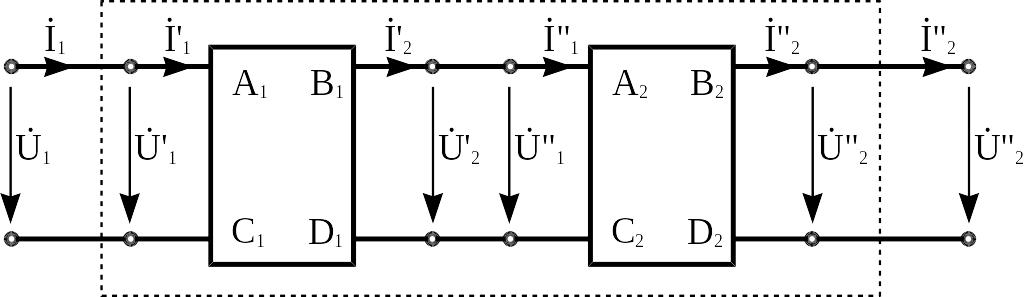
8. Каскадное соединение четырехполюсников.

Это такое соединение, когда выходные зажимы одного четырехполюсника соединяются с входными зажимами другого четырехполюсника. При каскадном соединении двух четырехполюсников уравнения удобнее записать в A-параметрах.

Пусть два четырехполюсника соединены каскадно, в общем случае принцип согласования не выполняется. Будем считать, что постоянные четырехполюсников известны. Необходимо найти постоянные эквивалентного четырехполюсника.

Запишем уравнения отдельных четырехполюсников.

Или в матричной форме. Здесь

Для заданной схемы соединения , а значит . С учетом этого соотношения для первого четырехполюсника можно записать.

Уравнение эквивалентного четырехполюсника в матричной форме Так как , то получим.

Таким образом, при каскадном соединении двух четырехполюсников матрица постоянных эквивалентного четырехполюсника равна произведению матриц постоянных отдельных четырехполюсников, входящих в данное соединение. При соединении нескольких четырехполюсников это правило остается в силе.