- •1 . Обратное включение четырехполюсников. Уравнения четырехполюсников при прямом и обратном включении.
- •2. Передаточные функции четырехполюсника.
- •3. Операционный усилитель с обратной связью. Вывод коэффициента усиления по напряжению Ku.
- •4. Четырехполюсники и их уравнения типа y, z, a. Связь между их параметрами.
- •5. Определение характеристических параметров симметричного четырехполюсника через сопротивления холостого хода и короткого замыкания.
- •6. Опытный способ определения a-параметров четырехполюсника.
- •7. Определение характеристических параметров несимметричного четырехполюсника через a-параметры.
- •8. Каскадное соединение четырехполюсников.
- •9. Уравнения четырехполюсника с гиперболическими функциями.
- •35. Переходные процессы при скачкообразном изменении емкости в цепи. Некорректные коммутации.
- •10. Вторичные параметры четырехполюсника.
- •11. Определение входного сопротивления четырехполюсника в режимах холостого хода и короткого замыкания при согласованной нагрузке, при произвольной нагрузке через первичные и вторичные параметры.
- •19. Полосовой фильтр и его характеристики.
- •12. Работа четырехполюсников с обратной связью.
- •13. Определение характеристических параметров симметричного четырехполюсника через a-параметры.
- •14. Типы электрических фильтров. Определение коэффициентов затухания и фазы, характеристического сопротивления zст(f) в функции частоты для низкочастотного фильтра.
- •15. Высокочастотные реактивные фильтры.
- •16. Низкочастотные реактивные фильтры.
- •17. Пассивные rc-фильтры. Коэффициенты передачи для низкочастотных и высокочастотных фильтров.
- •18. Активный низкочастотный rc-фильтр.
- •23. Включение электрической цепи на напряжение произвольной формы. Интеграл Дюамеля.
- •24. Возникновение переходных процессов и законы коммутации.
- •25. Операторный метод расчета переходных процессов. Рассмотреть включение цепи r-l на постоянное напряжение операторным методом.
- •Алгоритм расчета переходного процесса операторным методом.
- •26. Переходной, установившийся (принужденный) и свободный процессы. Классический метод расчета.
- •27. Алгоритм расчета переходного процесса классическим методом в цепи первого порядка на примере подключения r-c-цепи к источнику постоянного напряжения.
- •28. Алгоритм расчета переходного процесса классическим методом в цепи первого порядка на примере подключения r-l-цепи к источнику постоянного напряжения.
- •29. Законы Ома и Кирхгофа в операторной форме. Пояснить принципы составления операторных схем замещения.
- •3 6.Продолжение
- •30. Пути восстановления оригинала функции по известному ее операторному изображению.
- •31. Алгоритм расчета переходного процесса классическим методом в цепи первого порядка на примере подключения r-l-цепи к источнику синусоидального напряжения.
- •32. Алгоритм расчета переходного процесса классическим методом в цепи второго порядка на примере подключения r-l-c-цепи к источнику постоянного напряжения.
- •33. Законы Кирхгофа в операторной форме. Эквивалентные операторные схемы замещения.
- •36. Переходные процессы при скачкообразном изменении индуктивности в цепи. Некорректные коммутации. Первый обобщенный закон коммутации.
- •1. Обратное включение четырехполюсников. Уравнения четырехполюсников при прямом и обратном включении.
- •2. Передаточные функции четырехполюсника.
31. Алгоритм расчета переходного процесса классическим методом в цепи первого порядка на примере подключения r-l-цепи к источнику синусоидального напряжения.

-фаза коммутации
Рис. 1.6.
1. Записываем решение как сумму свободной и установившейся составляющих
.
2. Установившийся ток находим комплексным методом.

Находим свободную составляющую.
3.1. Определение
общего вида свободной составляющей
смотри в примере 1.![]()
3.2. Определяем постоянную интегрирования.
![]()
![]()
![]()
![]()
По первому закону
коммутации
имеем ток в цепи при t=0+
равным 0. Тогда
![]() ,
,
![]() .
.
Записываем ответ и строим график:

![]()
Рис. 1.7.
Здесь следует
заметить, что интенсивность переходного
процесса зависит ещё и от фазы коммутации.
Для параметров, приведённых на графике
имеет место близость к максимально
возможному переходному процессу при
фазе коммутации 180о.
При слабом затухании с увеличением
постоянной времени (![]() )
угол сопротивления 90о,
тогда при 180о
будет иметь место максимальная
интенсивность переходного процесса и
ток дросселя может достигать ударного
значения, равного удвоенной амплитуде
установившейся величины.
)
угол сопротивления 90о,
тогда при 180о
будет иметь место максимальная
интенсивность переходного процесса и
ток дросселя может достигать ударного
значения, равного удвоенной амплитуде
установившейся величины.
32. Алгоритм расчета переходного процесса классическим методом в цепи второго порядка на примере подключения r-l-c-цепи к источнику постоянного напряжения.

Рассмотрим два случая:
а)
![]() ;
;
б)
![]() .
.
Согласно изложенной в предыдущей лекции методике расчета переходных процессов классическим методом для напряжения на конденсаторе в цепи на рис. 3 можно записать
|
(1) |
Тогда для первого случая принужденная составляющая этого напряжения
|
(2) |
Характеристическое уравнение цепи
![]() ,
,
решая которое, получаем
![]() .
.
В зависимости от соотношения параметров цепи возможны три типа корней и соответственно три варианта выражения для свободной составляющей:
1.
![]() или
или
![]() ,
где
,
где
![]() -
критическое
сопротивление
контура, меньше которого свободный
процесс носит колебательный характер.
-
критическое
сопротивление
контура, меньше которого свободный
процесс носит колебательный характер.
В этом случае
|
(3) |
2.
![]() -
предельный случай апериодического
режима.
-
предельный случай апериодического
режима.
В
этом случае
![]() и
и
|
(4) |
3.
![]() -
периодический (колебательный) характер
переходного процесса.
-
периодический (колебательный) характер
переходного процесса.
В
этом случае
![]() и
и
|
(5) |
где
![]() -
коэффициент затухания;
-
коэффициент затухания;
![]() -
угловая
частота собственных колебаний;
-
угловая
частота собственных колебаний;
![]() -
период собственных колебаний.
-
период собственных колебаний.
Для апериодического характера переходного процесса после подстановки (2) и (3) в соотношение (1) можно записать
![]() .
.
Для
нахождения постоянных интегрирования,
учитывая, что в общем случае
![]() и
в соответствии с первым законом коммутации
и
в соответствии с первым законом коммутации
![]() ,
запишем для t=0 два уравнения:
,
запишем для t=0 два уравнения:
![]()
решая которые, получим
![]() ;
;
![]() .
.
Таким образом,
![]() .
.
Тогда ток в цепи
![]()
и напряжение на катушке индуктивности
![]() .
.
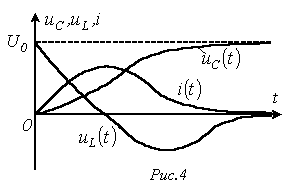
На
рис. 4 представлены качественные кривые
![]() ,
,
![]() и
и
![]() ,
соответствующие апериодическому
переходному процессу при
,
соответствующие апериодическому
переходному процессу при
![]() .
.
Для критического режима на основании (2) и (4) можно записать
![]() .
.
При
![]()
![]()
Таким образом
![]()
и
![]() .
.
Для колебательного переходного процесса в соответствии с (2) и (5) имеем
![]() .
.
Для
нахождения постоянных интегрирования
запишем
![]()
![]()
откуда
![]() и
и
![]() .
.
Тогда
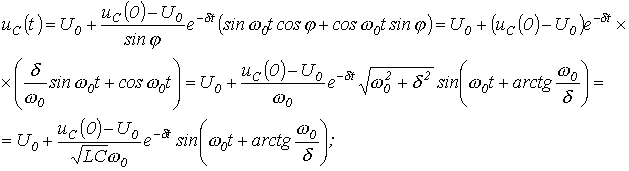
![]() .
.

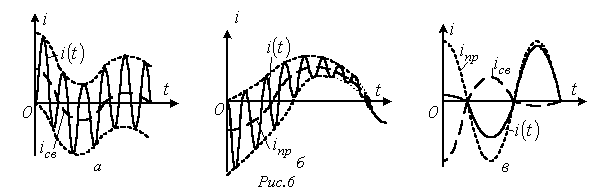
На рис. 5представлены качественные кривые и , соответствующие колебательному переходному процессу при .
При подключении R-L-C-цепи к источнику синусоидального напряжения для нахождения принужденных составляющих тока в цепи и напряжения на конденсаторе следует воспользоваться символическим методом расчета, в соответствии с которым
![]()
и
![]() ,
,
где
![]() ;
;
![]() ;
;
![]() .
.
Таким образом,
![]() и
и
![]() .
.
Здесь также возможны три режима:
1.
|
2.
|
3.
|
|
|
|
Наибольший
интерес представляет третий режим,
связанный с появлением во время
переходного процесса собственных
колебаний с частотой
![]() .
При этом возможны, в зависимости от
соотношения частот собственных колебаний
и напряжения источника, три характерные
варианта: 1 -
.
При этом возможны, в зависимости от
соотношения частот собственных колебаний
и напряжения источника, три характерные
варианта: 1 -
![]() ;
2 -
;
2 -
![]() ;
3 -
;
3 -
![]() ,
- которые представлены на рис. 6,а…6,в
соответственно.
,
- которые представлены на рис. 6,а…6,в
соответственно.