
- •1. Предмет и задачи автоматики
- •2. Основные понятия. Классификация сау. Принципы автоматического управления.
- •Принципы автоматического управления:
- •3. Законы управления
- •5. Задачи тау и характеристика процессов управления
- •6. Математическое описание линейных сау. Линеаризация. Формы записи ду.
- •7. Операторная форма записи линейных ду, передаточные функции, свойства преобразования лапласа
- •8. Динамические звенья и их характеристики
- •9. Временные характеристики
- •10. Понятие частотных характеристик
- •6.2. Частотные характеристики типовых звеньев
- •6.2.1. Безынерционное звено
- •6.2.2. Интегрирующее звено
- •6.2.3. Апериодическое звено
- •6.2.4. Инерционные звенья второго порядка
- •6.2.5. Правила построения чх элементарных звеньев
- •2.4.4. Частотные характеристики
- •11. Позиционные звенья и их характеристики
- •16. Алгебраические критерии устойчивости Необходимое условие устойчивости
- •Критерий Гурвица
- •17. Частотный критерий устойчивости. Критерий Михайлова
- •Частотный критерий. Критерий Найквиста
- •Частотный критерий устойчивости – логарифмический частотный критерий
- •Запасы устойчивости
- •18.Устойчивость систем обладающих запаздыванием
- •18. Метод d-разбиения
- •Теоретическое обоснование метода d-разбиений
- •19. Качества работы сау общие положения о качестве работы
- •20. Нелинейные системы
- •Метод фазовой плоскости. Особые точки и их типы.
- •Метод припасовывания
- •Метод гармонической линеаризации
- •Исследование устойчивости вторым методом ляпунова
- •Дискретные сау и особенности их математического описания.
Дискретные сау и особенности их математического описания.
Дискретные САУ.
Система управления называется дискретной, если она содержит дискретный элемент. Элемент называется дискретным, если его выходной сигнал квантован по времени или по уровню. Говорят, что сигнал квантован по времени, если он представляет собой последовательность импульсов, и квантован по уровню, если он принимает дискретные значения, т. е. значения, кратные некоторой минимальной величине, называемой уровнем квантования или квантом.
Дискретные системы разделяются на импульсные, цифровые и релейные.
Система управления называется импульсной, если она содержит импульсный элемент — дискретный элемент, преобразующий непрерывный сигнал в импульсный, т. е. в последовательность импульсов. На выходе импульсного элемента сигнал квантован по времени.
Система управления называется цифровой, если она содержит цифровое устройство. На выходе цифрового устройства сигнал квантован по уровню и по времени.
Система управления называется релейной, если она содержит релейный элемент. Релейные системы управления являются существенно нелинейными. Они не подлежат обычной линеаризации.
Импульсом
длительности
 называется сигнал (физическая величина),
который описывается функцией, не
обращающейся в нуль только на некотором
конечном интервале времени длительности
.
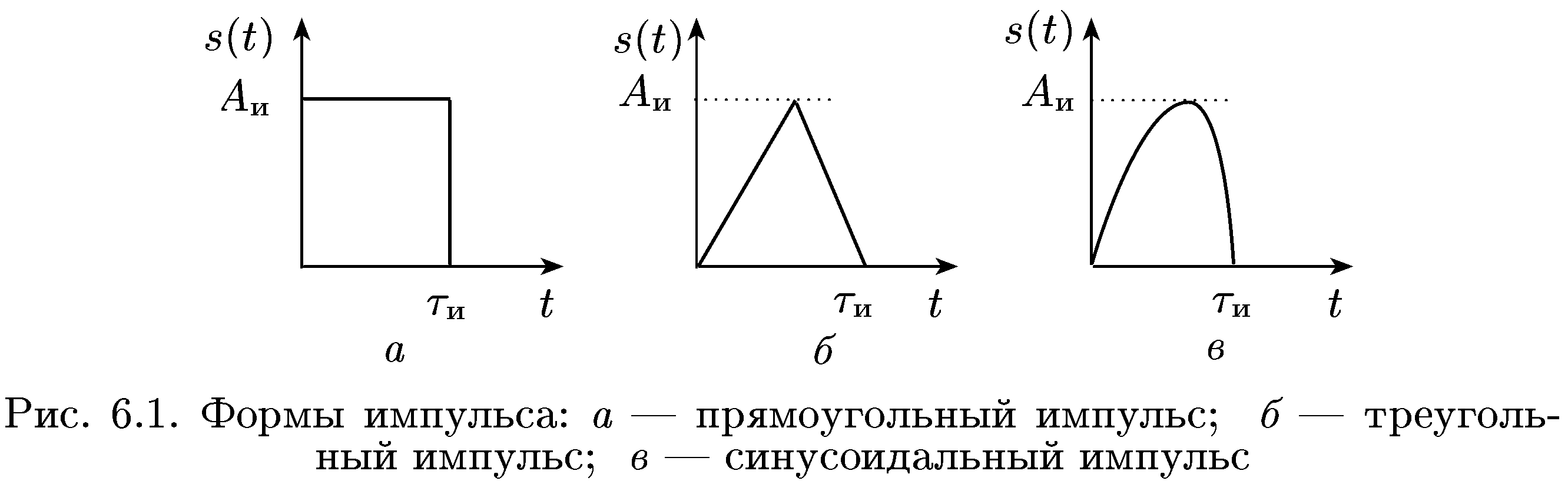
По форме различают прямоугольные,
треугольные, синусоидальные (рис. 6.1) и
другие импульсы. Они характеризуются
шириной (длительностью)
и амплитудой (высотой) АИ.
Последовательность импульсов, помимо
указанных параметров, еще характеризуется
периодом следования импульсов Т
и относительной длительностью
называется сигнал (физическая величина),
который описывается функцией, не
обращающейся в нуль только на некотором
конечном интервале времени длительности
.
По форме различают прямоугольные,
треугольные, синусоидальные (рис. 6.1) и
другие импульсы. Они характеризуются
шириной (длительностью)
и амплитудой (высотой) АИ.
Последовательность импульсов, помимо
указанных параметров, еще характеризуется
периодом следования импульсов Т
и относительной длительностью
![]()

В импульсном элементе происходит модуляция, т. е. в соответствии с входным сигналом изменяется один из параметров последовательности импульсов на выходе. В зависимости от того, какой параметр изменяется, различают амплитудно-импульсную модуляцию (АИМ), широтно-импульсную модуляцию (ШИМ) и другие. При АИМ изменяется амплитуда АИ, а при ШИМ — ширина (длительность) импульса. Импульсный элемент, осуществляющий амплитудно-импульсную модуляцию, называют АИМ-элементом, а импульсный элемент, осуществляющий широтно-импульсную модуляцию, называют ШИМ-элементом.
Импульсную систему управления, содержащую АИМ-элемент, называют АИМ-системой управления, а импульсную систему управления, содержащую ШИМ-элемент, называют ШИМ-системой управления.
Различают импульсную модуляцию 1-го и 2-го родов. При импульсной модуляции 1-го рода модулируемый параметр изменяется в соответствии со значениями входного (модулирующего) сигнала

(рис. 6.3, а) в дискретные моменты времени, называемые моментами съема сигнала (рис. 6.3,6).
При модуляции 2-го рода модулируемый параметр изменяется в соответствии со значениями модулирующего сигнала в течение всего времени существования импульса (рис. 6.3, в).
