Метод фазовой плоскости. Особые точки и их типы.
Метод фазовой плоскости — графоаналитический метод исследования динамических систем, приводимых к уравнениям вида:
Теоретические основы метода разработаны Пуанкаре и Ляпуновым, однако метод систематически не использовался до 1930х годов.
Обычно метод применяется для исследования нелинейных систем, в случаях, когда линеаризация приводит к неудовлетворительным ошибкам, либо когда линеаризация значительно ограничена в применимости по времени.
С помощью метода находят характеристики особых точек, изолированных замкнутых траекторий и сепаратрис, что в свою очередь позволяет оценить динамику разрабатываемой или исследуемой нелинейной динамической системы в широком диапазоне возможных начальных условий.
На рис.Фазовый портрет системы, устойчивой в большом, и неустойчивой в малом. Эллипс выделенный жирным — устойчивый предельный цикл, характеризующий автоколебания, и в данном случае являющейся сепаратрисой.
Особые точки и их типы.
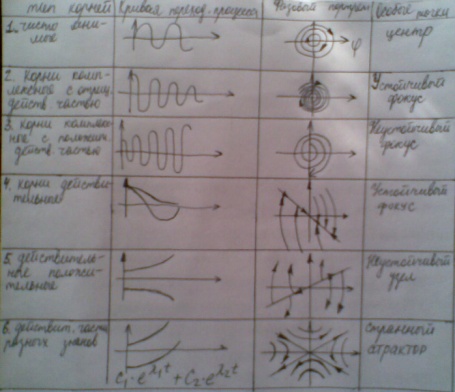
Метод припасовывания
Метод припасовывания
Часто нелинейные системы представляются как кусочно-линейные, т. е. их динамические свойства описываются линейными дифференциальными уравнениями, разными для разных участков процесса управления.
Метод припасовывания состоит в том, что линейные дифференциальные уравнения решаются в общем виде отдельно для каждого участка процесса, на котором они справедливы. Затем на каждом участке в полученных решениях произвольные постоянные определяются таким образом, чтобы все соседние участки правильно состыковывались друг с другом. Это делается следующим образом: по заданным начальным условиям процесса определяются произвольные постоянные в общем решении для первого участка. Значения фазовых координат в конце первого участка служат начальными условиями для второго участка и т. д.
Вообще говоря, описанная схема метода припасовывания может быть применена и тогда, когда какой-либо участок описывается нелинейным дифференциальным уравнением при условии, что известно его общее решение.
Проиллюстрируем
на простом примере использование метода
припасовывания для определения
переходного процесса и для определения
периодического решения (автоколебаний).
Дана система, схема которой изображена
на рис. 3.1, а, нелинейная характеристика
Р(х)
регулятора представлена на рис. 3.1б.
Уравнение объекта:
уравнение
регулятора:
Общее
уравнение замкнутой системы имеет вид:
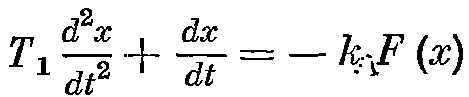
Определение переходного процесса. Представим себе примерно возможный качественный вид процесса:
(рис. 3.2). Он разбивается на участки АВ, ВD и т. д., внутри которых в соответствии с нелинейной характеристикой функция Р(х) принимает постоянные значения +с или —с. Изобразим отдельно участки АВ и ВD (рис. 3.3), отсчитывая время t на каждом из них от нуля.
На
участке АВ:
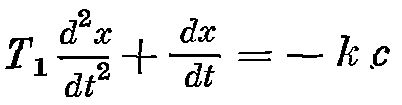,имеет
интеграл в виде
,второй
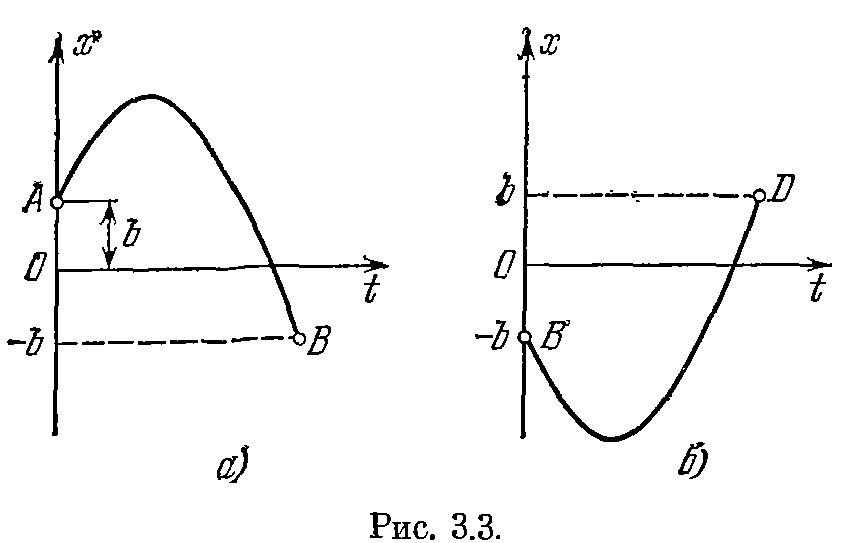начальные
условия:
,по
ним находим
На
участке BD:
,интеграл
первый
,второй
Начальные
условия для BD:
,получаем
.
На
след.за точкой D
снова будет решаться уравнение
