
- •1. Что является объектом изучения теории автоматического управления (тау). Перечислить основные задачи линейной тау.
- •4. Классификация систем автоматического управления в зависимости от: свойств входящих в систему элементов; природы функционирующих в системе сигналов; назначения системы управления.
- •6. Временные элементы линейных звеньев аср: переходная функция, переходная характеристика элемента. Обратное преобразование Лапласа. Формула разложения Хэвисайта. Нормированная передаточная функция.
- •7. Назначение структурных схем. Виды структурных схем. Элементы алгоритмических структурных схем.
- •8. Правила преобразования структурных схем: последовательное соединение звеньев; параллельное соединение; охват звена обратной связью.
- •9. Правила преобразования структурных схем: перенос сумматора; перенос узла (точки) разветвления. Правило Мейсона (Мэзона) преобразования структурных схем.
- •12. Логарифмические амплитудно-частотная и фазо-частотная характеристики.
- •16. Пропорционально-интегрально-дифференциальный (пид-) закон регулирования. Схемы реализации и переходные характеристики пи- и пид-законов регулирования.
- •17. Определить понятие «качество процессов регулирования». По каким показателям (критериям) оценивается качество процесса регулирования.
- •2 0. Показатели качества переходных процессов в системах регулирования. Прямые показатели качества переходных процессов при отработке задающих и возмущающих воздействий и их определение.
- •21. Косвенная оценка качества переходных процессов в системе регулирования по вещественной переходной характеристике замкнутой системы.
- •23. Интегральные оценки качества переходных процессов в системе регулирования. Линейная интегральная оценка, квадратичная интегральная оценка, улучшенная интегральная квадратичная оценка.
- •24. Критерии устойчивости систем регулирования. Ценность критериев устойчивости. Алгебраический критерий устойчивости Гурвица: исходные данные; формулировка.
- •26. Критерии устойчивости систем регулирования. Ценность критериев устойчивости. Частотный критерий устойчивости Найквиста: исходные данные; формулировка в случае неустойчивой разомкнутой системы.
- •27.Запас устойчивости системы регулирования
- •28. Критерии устойчивости систем регулирования. Ценность критериев устойчивости. Частотный критерий устойчивости Михайлова.
- •30. Устойчивость системы регулирования с запаздыванием
- •32. Частные задачи, решаемые при создании эффективных (качественных) систем регулирования. Корректирующие устройства. Стабилизация путем последовательной и параллельной коррекции.
- •33. Частные задачи, решаемые при создании эффективных (качественных) систем регулирования. Стабилизация путем использования местных обратных связей. Жесткие и гибкие обратные связи
- •35. Этапы (работы) предшествующие синтезу системы регулирования. Два варианта постановки задачи синтеза системы регулирования. Синтез систем методом логарифмических амплитудно-частотных характеристик.
- •37. Синтез систем регулирования методом модельного оптимума. Критерий оптимального модуля. Обоснование вида желаемой (базовой) передаточной функции замкнутой системы. Вывод условия оптимизации.
- •41. Синтез двухконтурных каскадных систем регулирования с использованием метода модального оптимума.
- •42. Модификация метода модального оптимума.
- •43. Синтез систем с дифференцированием сигнала из промежуточной точки на основе метода модального оптимума и упредителя Смита.
- •44. Синтез систем регулирования методом симметричного оптимума. Критерий оптимизации. Базовая передаточная функция. Вывод условий оптимизации.
- •47. Сглаживание задающего сигнала в системе синтезированной методом симметричного оптимума.
- •48. Сглаживание и дифференцирование задающего сигнала в системе синтезированной методом симметричного оптимума.
- •49. Оптимальное управление. Цель и задачи оптимального управления. Критерии качества. Формулировка задачи оптимального управления.
- •50. Адаптивное управление. Общие понятия об адаптивном управлении. Адаптация. Классификация адаптивных систем. Принципиальная схема адаптивной системы.
4. Классификация систем автоматического управления в зависимости от: свойств входящих в систему элементов; природы функционирующих в системе сигналов; назначения системы управления.
От свойств входящих в систему элементов:
Линейные
Линейные системы состоят из линейных элементов, модели которых могут быть описаны линейными ДУ. Линейные системы являются идеализированными, поскольку большинство реальных систем являются линейными только для определенного и достаточно узкого диапазона изменения действующего в них сигнала.
Нелинейные
Нелинейные системы включают в себя нелинейные элементы даже в рабочем диапазоне. Динамика нелинейных систем описывается нелинейными ДУ. Нелинейность возникает в силу различных причин (например, трение).
От природы функционирующих в системе сигналов:
Непрерывные
Регулирование в непрерывных системах производится непрерывно в зависимости от текущего значения ошибки регулирования. В непрерывных системах управляющие сигналы являются непрерывными функциями времени.
Дискретные В дискретных системах управляющий сигнал может представлять собой последовательность импульсов (импульсная система), цифровой код (цифровая система).
От назначения системы управления:
Системы автоматической стабилизации
Задающее воздействие – постоянная, заранее известная величина. Пример – система поддержания tº воздуха в холодильнике.
Системы программного управления
Задающее воздействие – переменная, заранее известная величина. На практике используются 2 вида: а) система с временной программой. Задатчик программы непосредственно вырабатывает Хзд(t). Пример – программное управление tº в закалочных печах. б) система с пространственной программой. Движение рабочего органа осуществляется по заданной в пространстве траектории. Пример – управление промышленным роботом.
Следящие системы. Задающее воздействие – переменная, заранее неизвестная величина.
5. Сущность принципа суперпозиции. Преобразование Лапласа. Модель элемента системы регулирования в виде линейного дифференциального уравнения. Передаточная функция элемента. Характеристический полином элемента (системы).
Принцип суперпозиции: Реакция системы Х(t) на линейную комбинацию воздействий (Xзд(t), F(t)) равна той же линейной комбинации реакции системы на каждое из этих воздействий в отдельности.
Преобразование Лапласа:
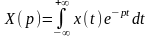
 ,
,
где x(t) – оригинал,
X(p) – изображение.

где L – оператор Лапласа.
Модель элемента:
В общем случае связь между входной x(t) и выходной y(t) величинами линейного элемента может быть описана линейным ДУ следующего вида:

Передаточная функция: Применим к ДУ преобразование Лапласа, при этом используя свойства линейности, дифференцирования и интегрирования.

 – передаточная
функция
– передаточная
функция
ПФ – отношение изображения по Лапласу выходного сигнала к изображению по Лапласу входного сигнала.
Характеристический полином: Многочлен знаменателя ПФ называют характеристическим полиномом элемента. Корни этого полинома определяют решение соответствующего ДУ при нулевых начальных условиях.
6. Временные элементы линейных звеньев аср: переходная функция, переходная характеристика элемента. Обратное преобразование Лапласа. Формула разложения Хэвисайта. Нормированная передаточная функция.
Наряду с дифференциальными уравнениями (ДУ) свойства элементов могут опред-ся их динамич хар-ми. Эти харак-ки определяют поведение элемента при некоторых заранее заданных типовых воздействиях. Наиболее частое воздействие – единичное ступенчатое воздействие.
С тупенчатое
воздействие выбирается по следующим
причинам как типовые:
тупенчатое
воздействие выбирается по следующим
причинам как типовые:
Ступенчатое воздействие относительно легко реализовать.
Считается, что такое воздействие является тяжелым для системы регулирования, ели она хорошо отрабатывает это воздействие, то она вполне нормально отрабатывает и другие воздействия.
Переходная функция: Функция, которая описывает поведение выходной величины элемента y(t), когда на вход подается единичное ступенчатое воздействие при нулевых начальных условиях. Переходная функция – аналитическое выражение для функции y(t), которое является решением ДУ элемента для единичного ступенчатого воздействия при нулевых начальных условиях.
Переходная характеристика элемента: График переходной функции y(t).
Обратное преобразование Лапласа: Если известно ДУ элемента, то можно определить переходную функцию и характеристику путем решения этого ДУ аналитическими методами. Однако в инженерной практике для решения такой задачи используют операционный метод:
 – передаточная
функция
– передаточная
функция

 –
обратное
преобразование Лапласа
–
обратное
преобразование Лапласа

Формула разложения Хэвисайта: Если корни характеристического полинома простые и некратные, то преобразование Лапласа можно выполнить с помощью формулы Хэвисайта:

Нормированная передаточная функция: Пусть
– передаточная функция

где
 – коэффициент усиления разомкнутой
системы.
– коэффициент усиления разомкнутой
системы.
Нормированная передаточная функция характеризуется тем, свободные члены числителя и знаменателя равны 1.
