35. Этапы (работы) предшествующие синтезу системы регулирования. Два варианта постановки задачи синтеза системы регулирования. Синтез систем методом логарифмических амплитудно-частотных характеристик.

(начало смотри вопрос 34).

Синтез систем методом логарифмических амплитудно-частотных характеристик.

Свойства системы регулирования полностью определяются частотными характеристиками разомкнутой цепи, при этом обычно достаточно рассмотреть только логарифмическую амплитудно-частотную характеристику.

Сущность метода заключается в следующем: сначала строится асимптотическая ЛАХ неизменной части системы, затем строится желаемая ЛАХ системы. Разность между этими характеристиками определяет логарифмическую АЧХ характеристику корректирующего устройства (регулятора), который необходимо добавить в систему.

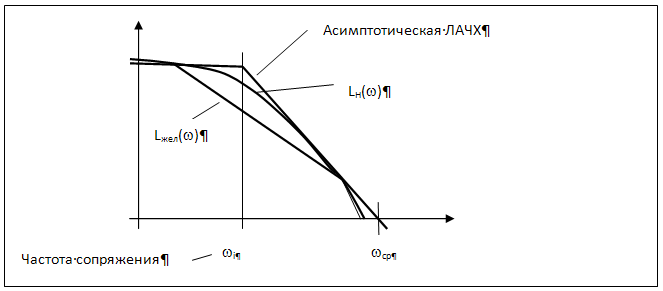
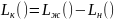
При этом неизменная часть системы включает объект регулирования, исполнительное устройство, датчик регулируемой величины и сравнительное устройство.

Желаемую ЛАХ условно разделяют на 3 части:

Низкочастотную

Среднечастотную

Высокочастотную

Среднечастотная часть является наиболее важной, она определяет устойчивость, запас устойчивости и, следовательно, качество переходного процесса.

Основными параметрами среднечастотной асимптоты является её полигон и частота среза.

Частота среза – частота, при которой желаемая ЛАЧХ пересекает ось частот.

Единицы измерения наклона асимптоты дБ/декада. Чем больше наклон средних частот асимптоты, тем труднее обеспечить хорошие динамические свойства системы. Поэтому наиболее целесообразно выбирать наклон 20 дБ/дек. при этом частота среза определяет быстродействие системы. Чем больше частота среза, тем меньше время регулирования.

Высокочастотная часть ЛАХ желаемой незначительно влияет на динамические свойства системы. Поэтому в ряде случаев при расчёте системы высокочастотная часть ЛАХ вообще не принимается во внимание.

Низкочастотная часть характеристики оказывает наибольшее влияние на статические свойства системы. Требования к статическим свойствам задачи в виде порядка астатизма (количество интегрирующих звеньев) и значением коэффициента усиления разомкнутой системы.

Отметим, что при синтезе метолом ЛАХ требования к системе задаются max допустимыми значениями перерегулирования и временем регулирования.

Метод ЛАХ позволяет определять передаточные функции корректирующих устройств, которые включают параллельно и встречно параллельно.

36. Синтез систем регулирования. Передаточные функции идеальной замкнутой системы регулирования. Критерии оптимизации контура регулирования (критерии синтеза): критерий устойчивости; критерий апериодической устойчивости.

Если данные и свойства объекта регулирования известны, т.е. известны математическая модель, то задача заключается в выборе типа регулятора и параметров его настройки, при которых формируемые регулятором управляющее воздействие будет в состоянии как можно быстрее, точнее и без возникновения колебаний заставить регулируемую величину y(t) следовать за задающим воздействием и нейтрализовать изменение возможного воздействия f₁(t). Идеальный режим контура регулирования достигнет в том случае, если бы регулируемая величина реагировала на задающее воздействие без запаздывания и без колебаний. Такое поведение будет иметь место, если передаточная функция будет равна:

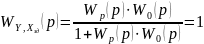
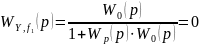
Препятствием для достижения такого идеального является инерционность объекта регулирования, обусловленная всеми его звеньями, поэтому возникает задача разработать и применить для данного объекта регулятор, наиболее подходящего типа с наилучшими параметрами настройки с тем, чтобы ликвидировать влияние инерционности объекта настолько полно, насколько это возможно. Такую задачу и называют организацией контура регулирования. Рассмотрим некоторые характерные варианты графиков переходных процессов при отработке задающего воздействия при разных параметрах настройки регулятора.

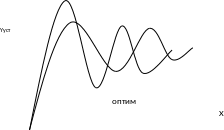
Оптимальным можно назвать вид переходного процесса при отработке задания, когда переход из одного состояния в другое происходит сравнительно быстро, а существенного перерегулирования или затягивания переходного процесса не наблюдается. Именно такой формы пытаются добиться путём правильного выбора типа регулятора и параметров его настройки. Обычно работу контура регулирования оценивают по реакции на ступенчатое задающее воздействие даже в тех случаях, когда в дальнейшем нас будет интересовать и обработка возмущающих воздействий. Реакция регулируемой величины на скачок X_зд позволяет правильно судить о том, насколько хорошо оптимизирован контур и по отношению к возбуждениям.

Выбор критерия оптимизации контура регулирования:

Первые проблемы с которыми сталкиваются при выборе типа регулятора и значение параметров его настройки – это выбор критерия или показателя качества регулирования. Все критерии качества в определённой степени являются произвольными из-за наличия в реальных системах регулирования нелинейностей, возмущений, приложенных к различным точками системы. Это приводит к тому, что более или менее оптимальные расчётные параметры регулятора всегда отличаются от значений, которые являются наилучшими для данной реальной системы. Различают 2 класса критерия в зависимости от того, применимы ли эти критерии при любых сигналах действующих на систему:

1. Универсальные критерии. Относятся:

   1. Критерий устойчивости.

   2. Критерий апериодической устойчивости.

   3. Критерий оптимального модуля и др.

2. Критерии при действии типовых внешних воздействий (ступени). Можно выделить:

   1. Прямые показатели качества

   2. Интегральной оценки качества переходных процессов и др.

Критерий устойчивости. Наиболее простой критерий, который основан на использовании знаменателя передаточной функции замкнутой системы, т.е используется не вся информация о системе, поскольку полином числителя тоже оказывает влияние на форму переходного процесса системы. Этот критерий применим как к системам первой, так и второй группы. Использование этого критерия основывается на таком выборе параметров регулятора, чтобы корни характеристического полинома возможно дальше отстояли от мнимой оси на плоскости корней.

Вопрос: Что этим обеспечивается? Ответ: запас устойчивости.

Этот критерий обеспечивает достаточно хорошую отработку как задающих воздействий, так и быструю ликвидацию отклонений, вызванных возбуждением. Математически доказано, что экстремализация этого критерия приводит к появлению в характеристическом полиноме корней большой кратности. В случае трансцендентных характеристических уравнений, имеющих бесконечное количество корней приводит к другому критерию синтеза, который называется критерием апериодической устойчивости.

Критерий апериодической устойчивости. Этот критерий требует, чтобы ближайший слева к мнимой оси корень был действителен и имел максимальную кратность. Критерий обеспечивает переходные процессы без перерегулирования с минимальным временем регулирования среди аналогичных процессов. Переходные процессы этого типа требуют слабого управления воздействия со стороны регулятора. Пример: Если речь идёт о ПИД регуляторе, то величины коэффициента усиления регулятора К_р и постоянная дифференцирования Т_д имеют маленькие значения, а постоянная интегрирования Т_и – большое.

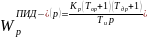
Этот критерий можно применять к таким системам, основная задача которых заключается в парировании внешних возмущений (системы стабилизации), а также к системам, основная задача которых является возможно более точное воспроизведение задающих воздействий (следящие системы). Они также применимы и для систем, которые в равной степени решают обе эти задачи.

Критерий оптимального модуля. Этот критерий использует информацию в числитиле и знаменателе передаточной функции замкнутой системы. Этот критерий обеспечивает выбор параметров настройки регулятора на основании следующих требований:

1. Полоса пропускания системы для полезного сигнала должна быть по возможности более широкой.

2. АЧХ замкнутой системы не должно иметь резонансного пика, а быть по возможности монотонно убывающей.

Переходные процессы в системе регулирования синтезируемые с помощью этого критерия отличаются небольшим временем регулирования и малым перерегулированием.

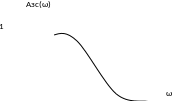
К выбору и обоснованию этого критерия оптимизации: мы сформулировали требования к синтезируемой системе регулирования.

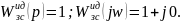
Система с такой формой АЧХ пропускает без искажений все частоты от 0 до бесконечности.

Примечание 1: в наиболее распространённых системах автоматического регулирования максимум АЧХ лежит в области низких частот, поэтому эти системы можно считать фильтрами низких частот.

Примечание 2: помехи и возмущающее воздействие имеют максимум спектра частот в высокочастотной области, которая должна лежать вне границы полосы пропускания системы.

Примечание 3: с точки зрения возможности точной отработки задающего воздействия система должна иметь широкую полосу пропускания, но с точки зрения подавления возмущений полоса пропускания должна быть узкой и согласованной со спектром возмущений таким образом, чтобы максимум этого спектра лежал вне полосы пропускания системы.

В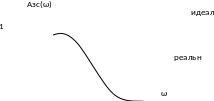 силу этих примечаний реальная система должна иметь такую форму АЧХ:

Вопрос: Что с чем связано, а именно время регулирования и время перерегулирования? Ответ: Время регулирования связано с полосой пропускания (чем шире полоса пропускания, тем меньше время), а перерегулирование связано с отсутствием «горба».

Таким образом в качестве критерия синтеза (оптимизации) при наличии сформулированных требований к системе можно выбрать критерий оптимального модуля.