Виток с током в магнитном поле. Закон ампера. Работа по перемещению проводника с током в магнитном поле.

Зако́н Ампе́ра — закон взаимодействия электрических токов. Впервые был установлен Андре Мари Ампером в 1820 для постоянного тока. Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Сила с которой магнитное поле действует на элемент объёма проводника с током плотности находящегося в магнитном поле с индукцией

Если ток течёт по тонкому проводнику, то где — «элемент длины» проводника — вектор, по модулю равный и совпадающий по направлению с током. Тогда предыдущее равенство можно переписать следующим образом:

Сила с которой магнитное поле действует на элемент проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока в проводнике и векторному произведению элемента длины проводника на магнитную индукцию

Направление силы определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощи правила правой руки.

Модуль силы Ампера можно найти по формуле:

Где — угол между векторами магнитной индукции и тока.

№14

Действие магнитного поля на движущийся заряд. Сила Лоренца.

Сила Лоренца- сила, действующая со стороны магнитного поля на движущуюся электрически заряженную частицу.

где q - заряд частицы;

V - скорость заряда;

B - индукции магнитного поля;

a - угол между вектором скорости заряда и вектором магнитной индукции.

Направление силы Лоренца определяется по правилу левой руки:

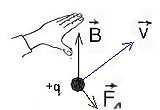
Если заряженная частица движется перпендикулярно силовым линиям магнитного поля, то сила Лоренца является центростремительной

№15

Циркуляция вектора магнитной индукции. Закон полного тока.

Теорема Ампера о циркуляции магнитного поля[5]:

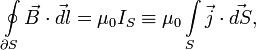
Теорема о циркуляции магнитного поля — одна из фундаментальных теорем классической электродинамики, сформулированная Андре Мари Ампером в 1826 году. В 1861 году Джеймс Максвелл снова вывел эту теорему, опираясь на аналогии с гидродинамикой, и обобщил ее (см. ниже). Уравнение, представляющее собой содержание теоремы в этом обобщенном виде, входит в число уравнений Максвелла. (Для случая постоянных электрических полей - то есть в принципе в магнитостатике - верна теорема в первоначальном виде, сформулированном Ампером и приведенном в статье первым; для общего случая правая часть должна быть дополнена членом с производной напряженности электрического поля по времени - см. ниже). Теорема гласит[1]:

Циркуляция магнитного поля постоянных токов по всякому замкнутому контуру пропорциональна сумме сил токов, пронизывающих контур циркуляции.

Эта теорема, особенно в иностранной или переводной литературе, называется также теоремой Ампера или законом Ампера о циркуляции (англ. Ampère’s circuital law). Последнее название подразумевает рассмотрение закона Ампера в качестве более фундаментального утверждения, чем закон Био — Савара — Лапласа, который в свою очередь рассматривается уже в качестве следствия (что, в целом, соответствует современному варианту построения электродинамики).

Для общего случая (классической) электродинамики формула должна быть дополнена в правой части членом, содержащим производную по времени от электрического поля (см. уравнения Максвелла, а также параграф «Обобщение» ниже). В таком дополненном виде она представляет собой четвёртое уравнение Максвелла в интегральной форме.

При анализе магнитных полей важное значение имеет закон полного тока, который в интегральной форме имеет вид:

и гласит о том, что линейный интеграл по замкнутому контуру l от напряженности магнитного поля равен полному току, протекающему сквозь сечение, ограниченное этим контуром.

Под полным током понимают алгебраическую сумму токов проводимости, переноса и смещения.

В дифференциальной форме закон полного тока можно записать следующим образом:

№16.