Раздел 4. Аэрометрические вычислительные комплексы

План раздела:

4.1. Аэрометрический метод определения параметров движения;

4.2. Системы воздушных сигналов;

4.3. Погрешности систем воздушных сигналов;

4.3.1. Методические погрешности СВС;

4.3.2. Инструментальные погрешности СВС.

4.1. Аэрометрический метод определения параметров движения

Аэрометрический метод определения движения основан на измерениях определенных аэрометрических величин, построении уравнений связи (уравнений метода) определяемых параметров и измеряемых величин и их решении. В соответствии с этим определяется и понятие навигационно-пилотажных систем воздушных сигналов (СВС). Первичными измеряемыми величинами являются: статическое давление атмосферы , динамическое давление набегающего потока воздуха (скоростного напора)и температура заторможенного потока воздуха.

Навигационно-пилотажные системы воздушных сигналов – устройства, предназначенные для определения параметров движения ЛА (самолетов, вертолетов) по отношению к воздушной среде, т.е. барометрической высоты, скорости полета, числа М и отклонений от заданных значений этих параметров, а также температуры наружного воздуха и относительной плотности воздуха.

В качестве уравнений связи в данном случае выступают определенные аэрометрические соотношения.

Скорость полета ЛА измеряют относительно воздушного потока и поверхности Земли. Различают истинную воздушную скорость – скорость полета ЛА относительно воздуха, индикаторную (приборную) скорость в предположении, что плотность воздуха одинакова на всех высотах, и путевую скорость – скорость полета ЛА относительно Земли. Безразмерной характеристикой скорости полета самолета является число , где– истинная скорость,– скорость звука в воздухе,– ускорение свободного падения,м/град – газовая постоянная,– абсолютная температура заторможенного потока воздуха в К,– показатель адиабаты для воздуха.

Уравнение связи для определения числа М при дозвуковой скорости полета

(4.1)

и при сверхзвуковой скорости полета

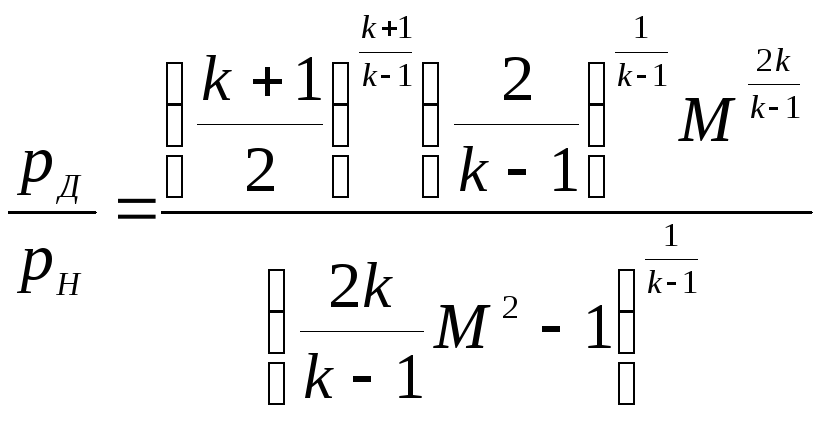, (4.2)

где ,– в Па. При значенииформулы (4.1) и (4.2) соответственно принимают вид

; (4.3)

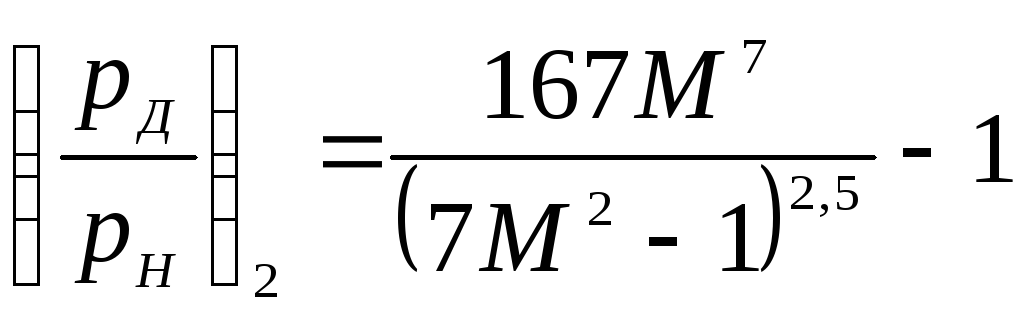. (4.4)

Уравнение связи для определения истинной воздушной скорости:

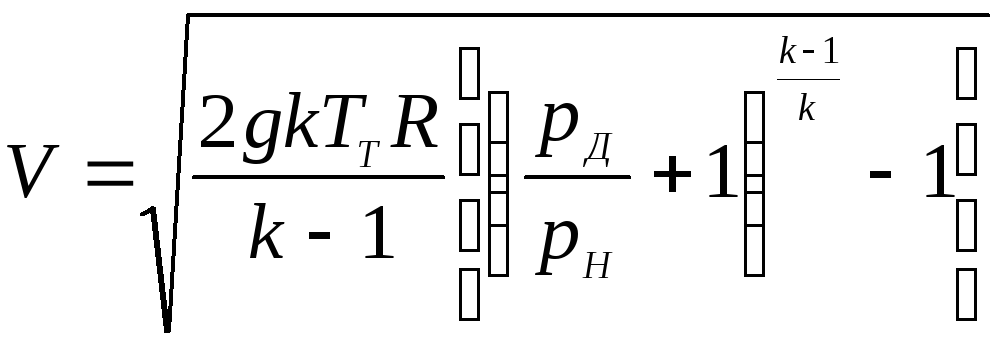(4.5)

или

, (4.6)

где ,– коэффициент торможения воздуха, значение которого в зависимости от конструктивных особенностей приемника и места его установки колеблется в пределах 0,98…1,02.

Уравнение связи для определения температуры наружного воздуха на высоте :

. (4.7)

Уравнение связи для определения барометрической высоты в соответствии с формулой Лапласа

. (4.8)

Величина средней температуры столба воздуха зависит от высоты и на средних широтах определяется зависимостями

для м, (4.9)

для м, (4.10)

где и– давление в Па и абсолютная температура воздуха в К у поверхности Земли,– давление на высоте 11000 м,– температура воздуха на высоте 11000 м.

Соотношение для определения относительной плотности воздуха

, (4.11)

где и– плотность воздуха соответственно а высотеи у поверхности Земли.

В уравнения связи (4.1)…(4.11) входят три переменные величины ,,. В результате измерения эти величины становятся известными функциями времени и в этом случае уравнения связи можно считать уравнениями функционирования СВС. В соответствии с изложенным на рис. 4.1 изображения схема системы СВС, где ИД, ИД, ИД– измерительные датчики соответственно величин,,;и– вводимые значения, соответствующие давлению и температуре атмосферы у поверхности Земли; У, У, У, У– дистанционные указатели соответствующих параметров (,,,); отдельными стрелками показаны выдаваемые электрические сигналы параметров (,,,,) и их приращений по сравнению с заданным режимом (,,).

Рис. 4.1. Схема системы воздушных сигналов

Сигналы измерительных датчиков поступают в вычислительное устройство, при помощи которого осуществляется построение решений уравнений функционирования. В зависимости от типа используемого вычислителя различают СВС аналогового и цифрового типа.