Раздел 9. Радионавигационные системы

План раздела:

9.1 Радионавигационные системы дальней навигации;

9.1.1. Особенности радиосистем дальней навигации;

9.1.2. Фазовые дальномерные РСДН;

9.1.3. Фазовые разностно-дальномерные РСДН;

9.1.4. Точность фазовых РСДН;

9.2. Радиосистемы ближней навигации и посадки;

9.2.1. Особенности радиосистем ближней навигации и посадки;

9.2.2. Канал дальности РСБН;

9.2.3. Канал азимута РСБН;

9.2.4. Радиосистемы посадки.

9.1 Радионавигационные системы дальней навигации

9.1.1. Особенности радиосистем дальней навигации

К радиосистемам дальней навигации (РСДН) относятся позиционные системы определения местоположения подвижных объектов (потребителей навигационной информации), дальность действия которых не ограничена дальностью прямой видимости и составляет тысячи километров. Несущие частоты сигналов РСДН лежат в пределах 10…100 кГц.

Все РСДН представляют собой пассивные многопозиционные системы, основу которых составляет сеть опорных передающих радиостанций, размещаемых в точках с известными координатами (радионавигационные точки РНТ). Опорные станции (ОС) в моменты излучают навигационные сигналы, по которым потребитель, имеющий только приемную аппаратуру и устройства обработки сигналов, находит свое местоположение. При этом он использует собственный эталон времени (опорный генератор), с помощью которого измеряется время приема приходящего от ОС навигационного сигнала. Моменты излучения сигналовсинхронизированы со шкалой Всемирного координированного времени (UTC).

Геометрическим элементом , измеряемым в РСДН, является расстояние от потребителей до ОС или разность таких расстояний до двух ОС, а информационный параметр сигнала – фаза несущей частоты. Поэтому эти системы относятся к классу фазовых дальномерных, квазидальномерных и разностно-дальномерных.

Особенности дальномерных систем. Системы этого класса требуют синхронной работы эталона времени ОС, задающего моменты , и опорного генератора потребителя, задающего моменты, в которые включается измеритель времени приема навигационного сигнала. При синхронной работе этих генераторов измеренное расстояние от потребителя до-й ОС

, (9.1)

где ,,– известные координаты ОС;,,– искомые координаты потребителя в некоторой, например, геоцентрической системе координат. Для вычисления трех координат потребителя необходимы три независимых уравнения, подобных (9.1), т.е. нужно измерить три дальностипо трем опорным станциям (=1, 2, 3). Обычно одна из координат (высота потребителя) известна, например по данным высотомера, и для расчета координат точки П (рис. 9.1,а), где находится потребитель, достаточно найти две линии положения ЛП (окружности) по дальностямидо опорных станцийис базой.

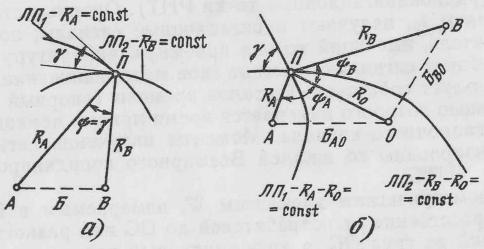
Рис. 9.1. Диаграммы определения местоположения на плоскости дальномерной (а) и разностно-дальномерной (б) системами

Особенности квазидальномерных систем. Такие системы используются при недостаточной стабильности опорного генератора потребителя, когда моменты излучения сигнала ОС и включения измерителя времени потребителя не соответствуют друг другу, т.е. имеется расхождение временных шкал системы и потребителя . Тогда измеренная потребителем дальностьотличается от истинной наи выражение (9.1) принимает вид

. (9.2)

Так как априори не известно, то для определения истинного местоположения необходимо увеличить на единицу число измерений расстояний до опорных станций. Системы, реализующие алгоритм (9.2), называются квазидальномерными, а величина– квазидальностью.

Точность дальномерных и квазидальномерных РСДН. Средняя квадратическая погрешность (СКП) определения местоположения связана с СКПизмерения элементасоотношением, где– геометрический фактор, характеризующий зависимость точности системы от взаимного положения потребителя и опорных станций. В дальномерной (квазидальномерной) системе геометрический фактор

. (9.3)

Особенности разностно-дальномерных систем. В этих системах измеряется разность расстояний до -й и-й опорный станций:

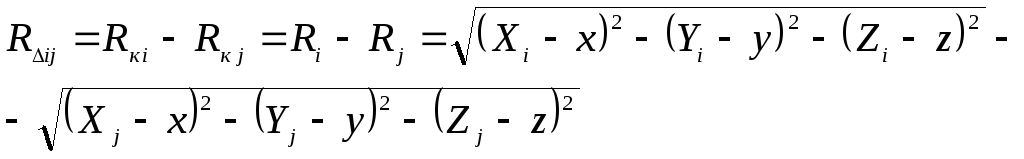(9.4)

Значение не зависит от, а следовательно, и от стабильности опорного генератора потребителя, что является основным преимуществом разностно-дальномерных систем. Для вычисления двух координат потребителя (при известной высоте последнего) нужно измерить две разности расстоянийипо трем ОС (на одну больше, чем в дальномерной системе). Положение точки П, в которой находится потребитель, рассчитывается по пересечению двух линий положения ЛП (гипербол), создаваемых опорными станциями,и(рис. 9.1,б).

Точность разностно-дальномерных систем. Геометрический фактор в системах этого класса

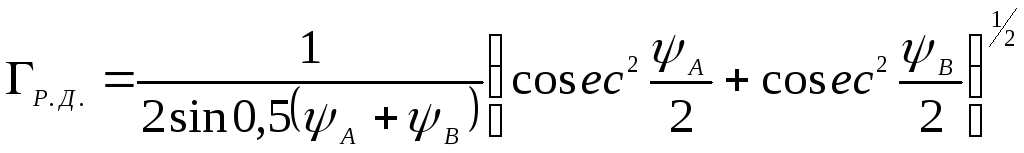. (9.5)

Углы, входящие в (9.5), показаны на рис. 9.1.

Из сравнения (9.3) и (9.5) очевидна большая зависимость геометрического фактора разностно-дальномерной системы от положения потребителя, чем в дальномерной системе, что объясняется расхождением гиперболических линий положения по мере удаления от базы системы, а следовательно, и увеличением линейной погрешности. Минимального значения геометрический фактор достигает при, что соответствует наивысшей точности системы. Дальномерная система обеспечивает требуемую точность (т.е. заданное значение геометрического фактора) в значительно большей зоне.