Раздел 3. Навигационные элементы

План раздела:

3.1. Навигационные системы координат;

3.1.1. Местные навигационные системы координат;

3.1.2. Глобальные системы координат;

3.2. Линии и поверхности положения. Линии пути;

3.3. Карты и картографические проекции;

3.3.1. Классификация и назначение авиационных карт;

3.3.2. Сущность картографических проекций и их классификация;

3.4. Курс и курсовые углы;

3.5. Навигационный треугольник скоростей.

3.1. Навигационные системы координат

В зависимости от масштабов перемещений системы отсчета могут быть местными, глобальными и космическими.

3.1.1. Местные навигационные системы координат

Местные системы координат (СК) используются в качестве систем отсчета при сравнительно небольших перемещениях, когда кривизной Земли можно пренебречь. По своей форме они могут быть:

– декартовы прямоугольные координаты;

– цилиндрические;

– сферические.

По ориентации осей местные СК можно разделить на:

– горизонтальные сферические;

– произвольные в азимуте;

– произвольные в пространстве.

В горизонтальной сферической СК за основную плоскость отсчета принята горизонтальная, перпендикулярная к линии отвеса. Положения ЛА (точка М) в этой СК определяется сферическими координатами; высотой , азимутоми длиной радиуса-вектора(рис. 3.1).

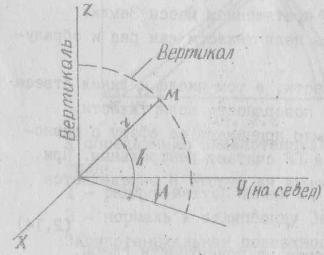
Рис. 3.1. Горизонтальная сферическая система координат

Высота отсчитывается как угол между горизонтальной плоскостью и направлением радиуса-вектора(положительное направление отсчета – вверх на горизонтальной плоскостью, отрицательное – вниз). Азимутотсчитывается в горизонтальной плоскости от северного направления географического меридиана по часовой стрелке до горизонтальной проекции радиус-вектора. Вертикальная плоскость, проходящая через радиус-вектор, называется вертикалом. Данная СК удобна для использования при полетах в районе аэродрома.

В горизонтальной цилиндрической (полярной) положение ЛА определяется в плоскости горизонта полярным (азимутальным) углом, радиусом-вектором и высотой над поверхностью Земли. Использование этой СК в навигационной системе счисления пути позволяет весьма просто осуществлять управление объектом из любой точки пространства непосредственно к заданной цели.

Произвольная в азимуте горизонтальная СК располагается в точке старта или финиша таким образом, чтобы одна из осей (например, ) была направлена в горизонтальной плоскости, например, по предполагаемой линии пути, а другая () – по вертикали.

СК с произвольной ориентацией осей может быть ориентирована относительно земного пространства таким образом, чтобы наиболее полно удовлетворять какой-либо конкретной навигационной задаче.

Местные СК находят широкое применение при счислении пути на небольшие расстояния порядка десятков и сотен километров, при управлении объектами в период взлета или посадки, при определении местонахождения относительно ориентиров, целей и промежуточных пунктов маршрута и т.п.

3.1.2. Глобальные системы координат

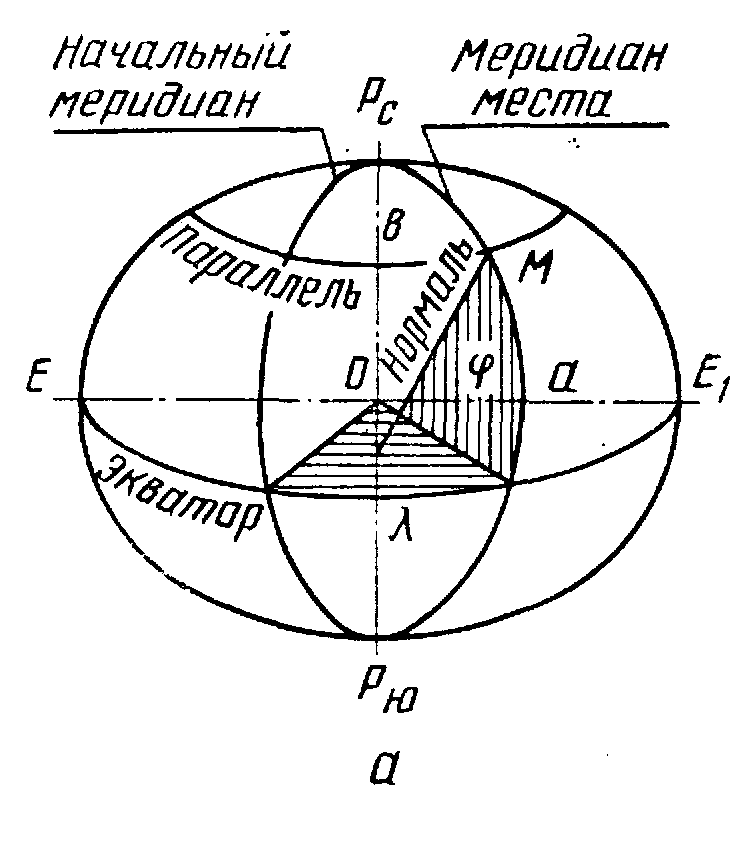
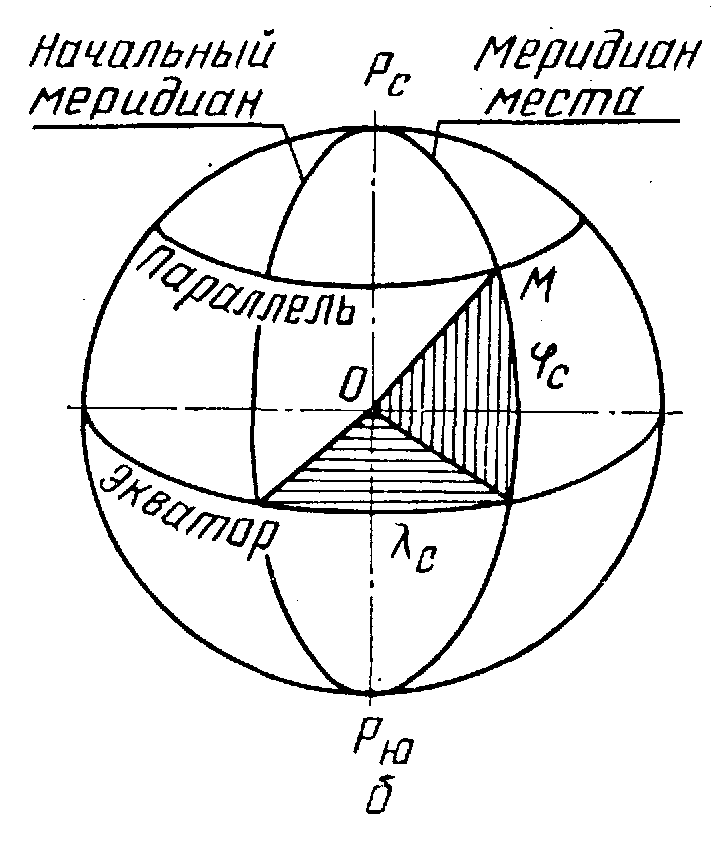
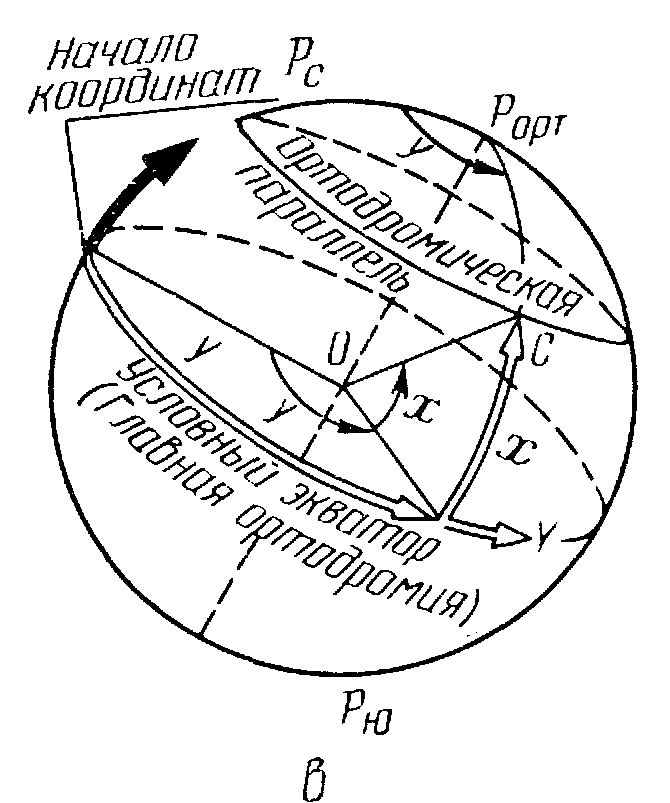
Глобальные СК жестко связаны с Землей и используются для навигации, охватывающей всю земную поверхность и околоземное пространство. Наиболее распространенными СК являются географическая (геодезическая), геоцентрическая (нормально сферическая) и ортодромическая (рис. 3.2).

а – географическая (геодезическая) СК	б – геоцентрическая (нормально сферическая) СК	в – ортодромическая СК

Рис. 3.2. Глобальные системы координат

В географической СК (рис. 3.2,а) используется земной геоид и за основную плоскость отсчета принята плоскость экватора. Географическая (геодезическая) широта определяется как угол между плоскостью экватора и отвесной линией (эта линия не проходит через центр Земли). Долготаопределяется как двугранный угол между плоскостью, образованной Гринвичским меридианом и меридианом, проходящим через точку М местонахождения ЛА.

Геоцентрическая СК отличается от географической способом отсчета широты. В геоцентрической СК Земля принимается за шар, а отсчет геоцентрической широты производится между плоскостью экватора и направлением радиус-вектора. Способ отсчета геоцентрической долготысовпадает со способом отсчета географической долготы.

Переход от географической СК к геоцентрической осуществляется с помощью соотношения

, . (3.1)

В ортодромической СК за основную плоскость отсчета принимают плоскость большого круга (ортодромию), а форму Земли – сферической. По существу эта СК по способу определения места ЛА аналогична геоцентрической, но отличается тем, что ее экватор и ось полюсов повернуты относительно земного экватора на определенный угол. Положение ортодромической системы относительно географической или геоцентрической задается двумя координатами полюса ортодромии. Местонахождение ЛА определяется ортодромической широтой, долготой, геоцентрическим радиусом-вектороми геоцентрической широтой и долготой полюса ортодромии,. Ортодромическая система координат удобна тем, что она позволяет осуществить навигацию от места старта до финиша по кратчайшему расстоянию – ортодромии. Для этого экватор ортодромической СК надо совместить с дугой большого круга, проходящего через точки старта и финиша на земной сфере.

При навигации ряда объектов применяются цилиндрические и прямоугольные декартовы СК, начало которых совмещено с центром Земли. Ориентация их координатных осей может совпадать с основными географическими направлениями (экватор, ось полюсов Земли, Гринвичский меридиан) или быть произвольной, подчиненной задачам навигации. Если навигация осуществляется не относительно Земли, а относительно какой-либо другой планеты или небесного тела, то в этом случае удобно применять аналогичные СК, связанные с этими небесными телами.

При использовании астрономических датчиков навигационной информации используются астрономические СК, основными из которых являются экваториальная и горизонтальная системы координат. Они тоже относятся к сферическим СК.

Кроме них, существует идеализированная СК – инерциальная. Она характеризуется поступательным, равномерным, и прямолинейным движением относительно звездного пространства.