Раскрытие красоты математических закономерностей

Пример 23. Золотое сечение.

С работ Декарта и Ферма алгебра стала широко использоваться в геометрических исследований. Вернемся к задачам на построение. Чтобы решить такую задачу алгебраическим методом, сначала составляют уравнение, связывающее искомую величину с данными. Затем решают это уравнение, т. е. находят формулу выражающую искомую величину через его коэффициенты, и про­изводят построение в соответствии с этой формулой.

В качестве примера решим задачу.

Построить правильный десятиугольник, вписанный в окружность радиуса r. (В «Началах» Евклида эта задача решается геометрически.)

Н ачнем с анализа. Пусть АВ = х – сторона правильного 10 - угольника (рис. 1). Центральный угол BOA составляет 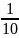часть полного, т.е. ВОА = 36⁰,

а ВАО = ОВА = 72⁰.

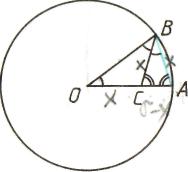
Рис. 1

D

r/2

В

Проведем биссектрису ВС угла ОВА (Получаемые при этом равные углы на рисунке отмечены одинаковыми дугами.) Тогда ОС = СВ = ВА = х, СА = г — х. Треугольники ОВА и ВАС подобны, поэтому

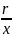= (1), откуда х² + r*x – r² = 0.

Уравнение имеет лишь одно положительное решение:

х=

O r А

Рис.2

Остается построить отрезок такой длины. Покажем, как это делается. Строится треугольник AOD, у которого АО = r, ОD =

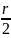
(рис. 2). Тогда AD = 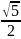r. Из отрезка AD вычитается отрезок BD = OD, в результате получается искомый отрезок

АВ = r - = r.

Заметим, что отношение ω = 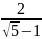= = 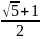1,6180339…

давно интересовало математиков. В Древней Греции деление отрезка длиной r на части х и r — х, для которых выполняется пропорция (1), получило название деления в среднем и крайнем отношении. Гораздо позже Леонардо да Винчи назвал такое деление золотым сечением, а Лука Пачоли — божественной пропорцией. По-видимому, такие названия связаны со многими замечательными свойствами сечения. Не последнюю роль в этом играли эстетические соображения: например, прямоугольник, отношение длин сторон которого равно ср, хорош для вос­приятия. Он называется прямоугольником золотого сечения. Близкими к прямоугольнику золотого сечения делают форматы книг.

Интересно, что если от такого прямоугольника отрезать квадрат максимальной площади, то останется вновь прямоуголь­ник золотого сечения. Это легко видеть из пропорции (1): отношение длины отрезка r к его большей части х равно ω, и отношение длины большей части х к меньшей r — х также равно ω.

Золотое сечение часто встречается в различных задачах. Рассмотрим одну из них.

Пример 24. Вписать в полукруг квадрат так, чтобы одна его сторона лежала на диаметре.

а

а

х

х

B

A

C

D

Рис.3

Для решения задачи, очевидно, достаточно найти точ­ку С (рис. 3). Оказывается, она осуществляет золотое сече­ние диаметра АВ. Покажем это. Обозначим АС =х, CD = a.

Тогда = откуда х² + ах — а² = 0, т. е. приходим к. из­вестному нам уравнению, определяющему золотое сечение.

П

B

B

ример 25. Построить правильный пятиугольник.

A

N

O

M

C

A

N

O

C

M

Рис.4

A

B

K

L

A

B

L

K

C

Рис.5

З ная, как разделить окружность на 10 равных частей, мы сумеем ее разделить и на 5 равных частей. Более Простой спо­соб построения правильного пятиугольника предложил древне­греческий ученый Клавдий Птолемей (ок. 100 — ок. 178). Он писал: «Имеем полукруг ABC (рис. 4), описанный около центра О на диаметре АОС. Проведем ОВ АС в точке О. Разделим отрезок ОС пополам в точке М, проведем прямую MB и отложим отрезок MN = MB. Соединим N с В прямой NB. Я утверждаю, что NO есть сторона правильного десятиуголь­ника, a NB — сторона правильного пятиугольника». (Конечно, Птолемей использовал для обозначения отрезков буквы греческо­го алфавита.)

Чтобы доказать утверждение Птолемея, выразим сторону а пятиугольника через радиус r описанной окружности. Вписан­ный угол, опирающийся на сторону правильного пятиугольника, равен 36°. Поэтому a = 2 r sin36°. Остается выразить в радикалах величину sin 36°. Из равенства

sin 36° = sin 144° = 2 sin 72° cos 72° = = 4 sin 36° cos 36° (2cos²36°— 1).

обозначив cos 36° = t, получаем: 1=4/(2/t²—1) или (2/t+1) (4t² — 2t— 1)=0.

Корнями этого уравнения являются t₁ = — , t_2,3 = .

Из них только один положительный, следовательно, cos36°= 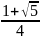откуда sin 36° = 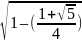² = 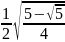, поэтому а = г

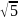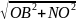Вернемся теперь к построению Птолемея. Так как NM = MB = = r/2 , то NO =NM – OM = ( . Как мы знаем, это сторона правильного десятиугольника, впи­санного в окружность радиуса r. Найдем теперь NB = = г , а это как раз сторона правильного пятиугольника.

Проведем в правильном пятиугольнике диагонали. Они обра­зуют пятиконечную звезду и обладают удивительным свойством: точки пересечения делят диагонали золотым сечением(рис. 5).

По-видимому, в связи с этим замечательным свойством пи­фагорейцы выбрали пятиконечную звезду в качестве своего та­лисмана: она считалась символом здоровья и служила опозна­вательным знаком. Бытует легенда о том, что один из пифаго­рейцев больным попал в дом к незнакомым людям; они старались выходить его, но болезнь не отступала. Не имея средств за­платить за лечение и уход, больной перед смертью попросил хозяина дома нарисовать у входа пятиконечную звезду, объяснив, что по этому знаку найдутся люди, которые вознаградят его. И на самом деле через некоторое время один из путешествующих пифагорейцев заметил звезду и стал расспрашивать хозяина дома, каким образом она появилась. После рассказа хозяина гость щедро вознаградил его.

Пифагорей­цы умели делить окружность циркулем и линейкой на 2^к+1, 2^к*3, 2^к *5,2^к*15 равных частей (k = 0, 1, 2, ...).