
- •Осн.Свойства и мех. Хар-ки жидкостей.
- •Абсол, избыт, атмосф давл и вакуум. Ед.Изм.
- •Приборы для опр давл и скорости течен жид.
- •Гидростат.Давл и его свойства.
- •Основное уравнение гидростатики.
- •9. Сила давл жидкости на плоскую стенку.
- •10. Давление жидкости на цилиндрическую поверхность.
- •Закона Паскаля и его применение
- •18. Энерг смысл ур-я Бернулли
- •19. Осн виды течения жидкости. Число Рейнольдса.
- •21. Кавитация
- •23. Распр. Скор при лам и торб режимах.
- •12. Уравнение неразрывности элементарной струйки идеальной жидкости.
- •40. Явление «Гидравлический удар». Уравнение н.Е. Жуковского.
- •8.Закон архимеда. Его существо и практическое применение.
- •16.Уравнение Бернули для потока реальной жидкости.
- •14. Геометр смысл Бернулли для струйки идеал жидк
- •15. Энерг смысл ур-я Берн для струйки идеальн жидк
- •25. Гидродинам подобие. Число Эйлера
- •24.Основы гидродинамического подобия
- •26. Гидродинам подобие. Число Рейнольдса
- •51. Истечение при несовершенном сжатии
- •29. Классификация трубопроводов
- •50. Истечение под уровень
- •46. Истечение через отверстия. Коэф напора
- •31. Простой трубопровод
12. Уравнение неразрывности элементарной струйки идеальной жидкости.
Рассмотрим элементарную струйку несжимаемой жидкости при установившемся движении. Выделим сечение 1-1 и 2-2, расположенные на расстоянии l одно от другого (рис.1.23). Здесь Δs1 и Δs2 - площади живых сечений соответственно; u 1 и u2 - скорости; ΔQ1 и ΔQ2 - расходы элементарной струйки в сечениях.
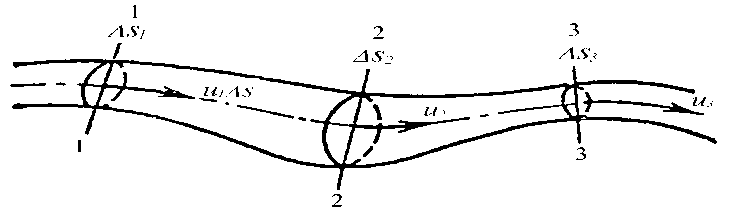
Очевидно, что ΔQ1 = Δs1u1 и ΔQ2 = Δs2u2, причем ΔQ1 втекает в рассматриваемый отсек, а ΔQ 2 - вытекает. Учитывая, что форма элементарной струйки не изменяется с течением времени, поперечный приток и отток невозможен, так как скорости на боковой поверхности струйки направлены по касательным к линиям тока, из которых состоит эта боковая поверхность, получаем, что расходы ΔQ1 и ΔQ2 равны, т.е. Δs1u 1 = Δs2u2. Аналогичные соотношения можно написать для любых двух сечений элементарной струйки, расположенных вдоль нее: u1Δs1 = u2Δs2 =...= uΔs = ΔQ = const. Это и есть уравнение неразрывности для элементарной струйки несжимаемой жидкости при установившемся движении. Если выделить в потоке два любых сечения, отстоящих на некотором расстоянии, то, просуммировав по каждому из живых сечений обе части в уравнении

Таким образом, в отмеченных условиях расход, проходящий через все живые сечения потока, неизменен, несмотря на то что в каждом сечении средняя скорость и площадь живого сечения могут быть различны.
![]() т.е.
средние скорости обратно пропорциональны
площадям живых сечений потока,
которым соответствуют эти средние
скорости.
т.е.
средние скорости обратно пропорциональны
площадям живых сечений потока,
которым соответствуют эти средние
скорости.
Кач-нное влиян темп на вязкость жидк и газа.
В
отличие от жидкостей, вязкость газов
увеличивается с увеличением температуры.
Формула
Сазерленда
может быть использована для определения
вязкости идеального
газа
в зависимости от температуры
![]() где:
μ
= динам вязкость в (Па·с) при заданной
темп T,
μ0
= контрольная вязкость в (Па·с) при
некоторой контрольной темп T0,
T
= заданная темп в К, T0
= контрольная темп в К, C
= постоянная Сазерленда для того газа,
вязкость которого требуется определить.
Эту формулу можно применять для темп
в диапазоне 0 < T
< 555 K и при давлениях менее 3,45 МПа с
ошибкой менее 10%, обусловленной
зависимостью вязкости от давления.
Вязкость
жидкостей
. Динамический
коэффициент вязкости.
Внутреннее трение жидкостей,
возникает при движении жидкости
вследствие переноса импульса в
направлении, перпендикулярном к
направлению движения. Справедлив общий
закон внутреннего трения — закон
Ньютона:
где:
μ
= динам вязкость в (Па·с) при заданной
темп T,
μ0
= контрольная вязкость в (Па·с) при
некоторой контрольной темп T0,
T
= заданная темп в К, T0
= контрольная темп в К, C
= постоянная Сазерленда для того газа,
вязкость которого требуется определить.
Эту формулу можно применять для темп
в диапазоне 0 < T
< 555 K и при давлениях менее 3,45 МПа с
ошибкой менее 10%, обусловленной
зависимостью вязкости от давления.
Вязкость
жидкостей
. Динамический
коэффициент вязкости.
Внутреннее трение жидкостей,
возникает при движении жидкости
вследствие переноса импульса в
направлении, перпендикулярном к
направлению движения. Справедлив общий
закон внутреннего трения — закон
Ньютона:
![]() Коэф вязкости
Коэф вязкости
![]() (динамическая
вязкость) может быть получен на основе
соображений о движениях молекул.
будет
тем меньше, чем меньше время t «оседлости»
молекул. Это приводит к выражению для
коэф вязкости, называемому ур-ем
Френкеля-Андраде:
(динамическая
вязкость) может быть получен на основе
соображений о движениях молекул.
будет
тем меньше, чем меньше время t «оседлости»
молекул. Это приводит к выражению для
коэф вязкости, называемому ур-ем
Френкеля-Андраде:
![]() .
Иная формула, представляющая коэф
вязкости, была предложена Бачинским.
Как показано, коэф вязкости определяется
межмолекулярными силами, зависящими
от среднего расстояния между молекулами;
последнее определяется молярным объёмом
вещества
.
Иная формула, представляющая коэф
вязкости, была предложена Бачинским.
Как показано, коэф вязкости определяется
межмолекулярными силами, зависящими
от среднего расстояния между молекулами;
последнее определяется молярным объёмом
вещества
![]() .
Эксперименты показали, что между
молярным объёмом и коэф вязкости сущ-ет
соотношение
.
Эксперименты показали, что между
молярным объёмом и коэф вязкости сущ-ет
соотношение
![]() где с и b — константы. Это эмпирическое
соотношение называется формулой
Бачинского.
Динамическая вязкость жидкостей
уменьшается с увеличением температуры,
и растёт с увеличением давления.
Кинематическая
вязкость.
В технике, часто приходится иметь дело
с величиной
где с и b — константы. Это эмпирическое
соотношение называется формулой
Бачинского.
Динамическая вязкость жидкостей
уменьшается с увеличением температуры,
и растёт с увеличением давления.
Кинематическая
вязкость.
В технике, часто приходится иметь дело
с величиной![]() и
эта величина получила название
кинематической вязкости. Здесь
и
эта величина получила название
кинематической вязкости. Здесь
![]() —
плотность
жидкости;
—
динамическая вязкость. Кинематическая
вязкость в старых источниках часто
указана в сантистоксах (сСт). В систему
СИ
эта величина переводится следующим
образом: 1 сСт = 1мм2
—
плотность
жидкости;
—
динамическая вязкость. Кинематическая
вязкость в старых источниках часто
указана в сантистоксах (сСт). В систему
СИ
эта величина переводится следующим
образом: 1 сСт = 1мм2![]() 1c
= 10-6
м2
c.
Ньютоновские
и неньютоновские жидкости.
Ньютоновскими называют жидкости, для
которых вязкость не зависит от скорости
деформации. В уравнении
Навье — Стокса
для ньютоновской жидкости имеет место
аналогичный вышеприведённому закон
вязкости (по сути, обобщение закона
Ньютона, или закон
Навье):
1c
= 10-6
м2
c.
Ньютоновские
и неньютоновские жидкости.
Ньютоновскими называют жидкости, для
которых вязкость не зависит от скорости
деформации. В уравнении
Навье — Стокса
для ньютоновской жидкости имеет место
аналогичный вышеприведённому закон
вязкости (по сути, обобщение закона
Ньютона, или закон
Навье):![]() где
где
![]() —
тензор
вязких напряжений. Среди неньютоновских
жидкостей,
по зависимости вязкости от скорости
деформации различают псевдопластики
и дилатантные
жидкости.
Моделью с ненулевым напряжением сдвига
(действие вязкости подобно сухому
трению)
является модель
Бингама.
Если вязкость меняется с течением
времени, жидкость называется тиксотропной.
—
тензор
вязких напряжений. Среди неньютоновских
жидкостей,
по зависимости вязкости от скорости
деформации различают псевдопластики
и дилатантные
жидкости.
Моделью с ненулевым напряжением сдвига
(действие вязкости подобно сухому
трению)
является модель
Бингама.
Если вязкость меняется с течением
времени, жидкость называется тиксотропной.
|
Неустановившимся (нестационарным) движением жидкости называется такое движение, при котором в каждой данной точке основные элементы движения жидкости – скорость движения и и гидродинамическое давление р – постоянно изменяются, т.е. зависят не только от положения точки в пространстве, но и от времени
Примером установившегося движения может быть: движение жидкости в канале, в реке при неизменных глубинах, истечение жидкости из резервуара при постоянном уровне жидкости в нем и др. Неустановившееся движение – это движение жидкости в канале или реке при переменном уровне или при опорожнении резервуара, когда уровень жидкости в нем непрерывно изменяется.
