Вопрос 1

1) Площадь треугольника

2. Формула Герона.

П лощадь треугольника равна , где p - полупериметр и a, b, c - стороны  этого треугольника.

Условие:

Δ ABC

Доказательство:

Проведём высоту AD.

Пусть BC=a, AC=b, AB=c, AD=h, BD=x, тогда CD=a-x.

  ПотеоремеПифагора AD²=AB²-CD² и AD²=AC²-CD² => AB²-BD²=AC²-CD², т. е. с²-x²=b²-(a-x)² => 2ax=a²+c²-b².

По теореме Пифагора AD²=AB²-BD² => h²=c²-x²

Последовательно разложив на множители как разности квадратов в числителе, получаем, что

Пусть периметр (a+b+c) треугольника АВС будет равен 2р =>

=>

a+b-c=2p-2c

 a+c-b=2p-2b

b+c-a=2p-2a

Мы знаем, что S= =>S=

Вопрос 2

Пусть О(х;у) – середина отрезка А(х₁;у₁)В(х₂;у₂)

Если отрезок параллелен прямой ОХ, то у₁=у₂=у.

Если отрезок параллелен прямой ОУ, то х₁=х₂=х.

Билет №18 1. Вывод формулы площади параллелограмма. 2. Вывод формулы радиуса описанной и вписанной окружности (для треугольника).

Вопрос 1

Пусть АВСD – данный параллелограмм. Если он не является прямоугольником, то один из его углов острый или тупой. Пусть он будет острым.

Опустим перпендикуляр АЕ на прямую СD. Тогда площадь трапеции АВСЕ равна сумме площадей параллелограмма АВСD и треугольника АDЕ.

Опустим перпендикуляр ВF на прямую СD. Тогда площадь трапеции АВСЕ равна сумме площадей параллелограмма АВFE и треугольника ВСF.

Треугольник ADE и BCF равны, значит, имеют равную площадь, отсюда следует, что площадь параллелограмма равна площади прямоугольника ABFE, значит она равна АВ*ВF. Отрезок BF называется высотой параллелограмма, соответствующей сторонам АВ и СD.

Площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне.

Вопрос 2

Доказательство: 

По свойству 2 площади простой фигуры имеем

Отсюда имеемr=S/p.

Доказательство: По формуле 1   по теореме синусов   т. е. 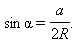  Подставляя выражение для   в формулу для площади треугольника, получим искомую формулу. Т.е. .

Билет №19 1. Трапеция (определение).Вывод формулы площади трапеции. Теорема о средней линии трапеции.

2. Уравнение окружности (вывод). Взаимное расположение прямой и окружности в координатах. Вопрос 1

Трапеция – это четырёхугольник, у которого одна пара противолежащих сторон параллельна.

Пусть АВСD – данная трапеция. Диагональ АС разбив. Её на два данных треугольника: АВС и СDА. Следовательно, площадь трапеции рвана сумме их площадей. Высоты СЕ и AF этих треугольников равны расстоянию между параллельными прямыми АВ и СD. Это расстояние называется высотой трапеции.Значит, площадь трапеции равна произведению её средней линии на высоту.

Теорема 6.8: Средняя линия треугольника и трапеции параллельна основании и равна её половине.

Доказательство: Пусть АВСD – данная трапеция. Проведём через вершину В и середину Р боковой стороны СD прямую. Л на пересекает прямую АD в некоторой точке Е. Треугольники РВС и РЕD равны по второму признаку. Из равенства треугольников следует равенство их сторон: РВ=РЕ, ВС=ED.Значит, средняя линия трапеции PQ является средней линией АВУ, а значит PQ||AE и PQ=0.5(AD+BC).