
- •Вопрос 1.
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
Вопрос 2
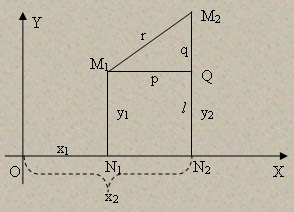
Расстояние между двумя точками в координатах Лобачевского. Пусть даны две точки M1(x1,y1) и M2(x2,y2). Опустим из этих точек перпендикуляры M1N1 и M2N2 на ось X и M1Q┴M2N2 (рис. 10). Введём обозначение: M1Q=p, M1M2=r, M2Q=q, N2Q=l. Пусть y2>y1. Тогда из прямоугольного треугольника M1M2Q получаем на основании формулы (2)
![]()
но так как q=y2–l, то

Из четырёхугольника Ламберта N2N1M1Q на основании формулы (19) находим
![]()
на основании формулы (18)
![]()
Подставив эти выражения в предыдущие равенства, получим
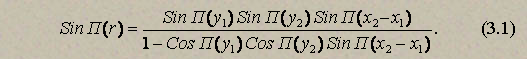
Так как SinП(x2–x1)=SinП(x1–x2), то это выражение симметрично относительно координат обеих точек, и условие y2>y1 не является обязательным.
Формулу (3.1) на основании равенства (12) можно привести к виду
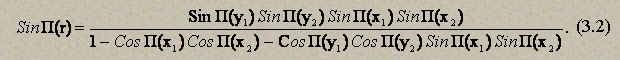
Формула расстояния между двумя точками значительно упрощается в бельтрамиевых координатах.
Билет №9 1. Признаки равенства прямоугольных треугольников (доказательство всех признаков). 2. Окружность (определение). Формула для вычисления длины окружности (без вывода).Вывод формулы длины дуги окружности.
Вопрос 1
Так
как в прямоугольном треугольнике угол
между двумя катетами — прямой, а любые
два прямых угла равны, то из первого
признака равенства треугольников
следует, что:
если катеты одного прямоугольного
треугольника соответственно равны
катетам другого прямоугольного
треугольника, то такие треугольники
равны.
Из
второго признака равенства треугольников
следует, что:
если катет и прилежащий к нему острый
угол одного прямоугольного треугольника
соответственно равны катету и прилежащему
к нему острому углу другого прямоугольного
треугольника, то такие треугольники
равны.
Рассмотрим еще два признака равенства
прямоугольных треугольников:
если гипотенуза и острый угол одного
прямоугольного треугольника соответственно
равны гипотенузе и острому углу другого
прямоугольного треугольника, то такие
треугольники равны.
Доказательство. Из теоремы о сумме углов
треугольника следует, что в этих
треугольниках два других острых угла
также равны, поэтому они равны по второму
признаку равенства треугольников, т.
е. по стороне (гипотенузе) и двум прилежащим
к ней углам.
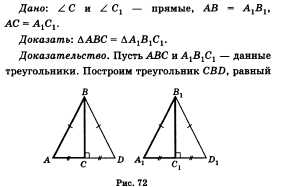
[П] Если гипотенуза и катет одного
прямоугольного треугольника равны
гипотенузе и катету другого прямоугольного
треугольника, то такие треугольники
равны.

 Вопрос
2
Вопрос
2
Окружность – это геометрическое место точек, равноудалённых от данной.
Длина окружности.
Периметр любого правильного вписанного в окружность многоугольника является приближенным значением длины окружности. Чем больше число сторон такого многоугольника, тем точнее это приближенное значение, так как многоугольник при увеличении числа сторон все ближе и ближе «прилегает» к окружности. Точное значение длины окружности — это предел, к которому стремится периметр правильного вписанного в окружность многоугольника при неограниченном увеличении числа его сторон.
Выведем формулу, выражающую длину окружности через ее радиус. Пусть С и С' — длины окружностей радиусов К и К'. Впишем в каждую из них правильный n-угольник и обозначим через Рn и Р'n их периметры, а через ап и а их стороны. Используя формулу (2) (см. «Подробнее», «Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности.»), получаем:
Рn = n•аn = n•2Rsin180/n,
Р'n =n•а’n = n•2R’sin180/n.
Следовательно,
Pn/P’n = 2R/2R’ (1)
Это равенство справедливо при любом значении n. Будем теперь неограниченно увеличивать число n. Так как Рn →С, Р' →C’ при n → ∞, то предел отношения Pn/P’n равен С/С’. С другой стороны, в силу равенства (1) этот предел равен 2R/2R’. Таким образом, С/С’ = 2R/2R’. Из этого равенства следует, что С/2R = C’/2R’, т.е. отношение длины окружности к ее диаметру есть одно и то же число для всех окружностей. Это число принято обозначать греческой буквой π..
Из равенства С/2R = π получаем формулу для вычисления длины окружности радиуса R.
С = 2πR.
Выведем теперь формулу для вычисления длины l дуги окружности с градусной мерой α. Так как длина всей окружности равна 2πR, то длина дуги в 1˚ равна 2πR/360 = πR/180. Поэтому длина l выражается формулой
l = πR/180 • α
Билет №10 1. Признаки параллелограмма с доказательствами.
2. Построение треугольника по трем сторонам.
