
- •Вопрос 1.
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
Вопрос 1
Теорема 4.5: Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Доказательство: Пусть АВС – данный треугольник. По теореме о сумме углов треугольников сумма углов А, В, и С равна 180, значит А+В=180-С, а 180-С ни что иное, как градусная мера внешнего угла при вершине С. Теорема доказана.
Внешним углом выпуклого многоугольника при данной вершине называется угол, смежный внутреннему углу многоугольника при этой вершине. В общем случае внешний угол это разность между 180° и внутренним углом.
Сумма внешних углов n-угольника равна 360°.
Сумма всех углов n-угольника равна 180°*n, а сумма внутренних углов n-угольника равна (n-2)*180°.
Значит, сумма внешних углов равна: 180n-(n-2)180=360°.
Вопрос 2
Рассмотрим
прямоугольный равнобедренный треугольник
с углом при основании, равным 45°. Пусть
катеты его равны a . Тогда по теореме
Пифагора его гипотенуза будет
равна ![]() Поэтому
Поэтому 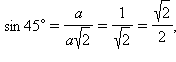
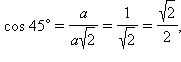

Билет №7 1. Геометрическое место точек. Теорема о геометрическом месте точек, равноудаленных от двух данных точек, в геометрической и аналитической формах. 2. Круг(определение). Формула для вычисления площади круга(без вывода). Вывод формулы площади кругового сектора.
Вопрос 1
Геометрическое место точек – фигура, которая состоит из всех точек на плоскости, обладающим определённым свойством.
Теорема: Геометрическое место точек, равноудаленных от двух данных точек, есть прямая, перпендикулярная к отрезку, соединяющему эти точки, и проходящая через его середину.
Вопрос 2
Круг — геометрическое место точек плоскости, расстояние от которых до заданной точки, называемой центром круга, не превышает заданного неотрицательного числа, называемого радиусом этого круга.
Теорема 1
Площадь
круга радиуса
![]() равна
равна
![]() .
.
Теорема 2
Площадь сектора равна произведению длины дуги сектора на половину радиуса.
Площадь
сектора с центральным углом в
![]() равна
равна
![]() ,
а площадь сектора
,
а площадь сектора
![]() с
углом
с
углом
![]()
![]() .
Выделим в этой формуле длину дуги
сектора
.
Выделим в этой формуле длину дуги
сектора
![]() ;
;
![]() .
.
Теорема доказана.
Билет №8 1. Треугольник (определение). Теорема о сумме углов треугольника.
2. Выражение расстояния между двумя точками через координаты этих точек (рассмотреть все случаи).
Вопрос 1
Треугольник – это три точки, не лежащие на одной прямой, и отрезки, попарно пересекающие их.
Сумма углов треугольника равна 180°. Доказательство : Пусть ABC' — произвольный треугольник. Проведем через вершину B прямую, параллельную прямой AC (такая прямая называется прямой Евклида). Отметим на ней точку D так, чтобы точки A и D лежали по разные стороны прямой BC.Углы DBC и ACB равны как внутренние накрест лежащие, образованные секущей BC с параллельными прямыми AC и BD. Поэтому сумма углов треугольника при вершинах B и С равна углу ABD.Сумма всех трех углов треугольника равна сумме углов ABD и BAC. Так как эти углы внутренние односторонние для параллельных AC и BD при секущей AB, то их сумма равна 180°. Теорема доказана.
