- •Вопрос 1.
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
Вопрос 2
Анализ. Если A ![]() a,
то задача не имеет решения, поэтому,
пусть A лежит
вне прямой a,
и b || a –
искомая прямая. Через точку A проведем
секущую (AB), B
a.
По свойству параллельных прямых
внутренние накрест лежащие углы при
параллельных прямых и секущей равны.
Верно и обратное: если внутренние накрест
лежащие углы при прямыхa и b и
секущей AB равны,
то a || b.
Отсюда способ построения.
a,
то задача не имеет решения, поэтому,
пусть A лежит
вне прямой a,
и b || a –
искомая прямая. Через точку A проведем
секущую (AB), B
a.
По свойству параллельных прямых
внутренние накрест лежащие углы при
параллельных прямых и секущей равны.
Верно и обратное: если внутренние накрест
лежащие углы при прямыхa и b и
секущей AB равны,
то a || b.
Отсюда способ построения.
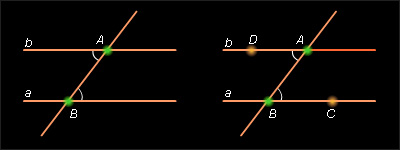
Построение. Через заданную точку A и произвольную точку B прямой a проведем прямую AB. Пусть C – произвольная, отличная от B точка прямой a. Построим от луча AB в полуплоскость, не содержащую точку C, угол, равный углу (ABC). Пусть [AD) – сторона построенного угла. Тогда прямая AD || a.
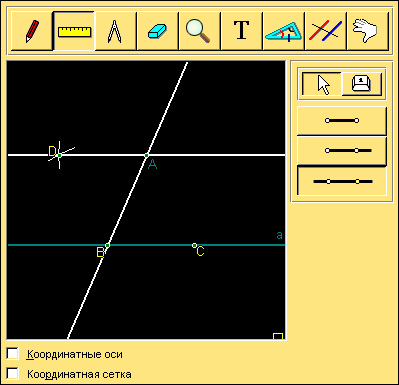
Через точку A проведите прямую, параллельную данной.
|
Модель 8.9. Построение прямой, параллельной данной. |
Доказательство:
Доказательство следует из признака параллельности прямых (теорема 3.1), ввиду равенства углов (ABC) и (BAD) как внутренних накрест лежащих при прямых a, (AD) и секущей (AB).
|
Билет №22
1. Теорема косинусов. 2. Деление отрезка пополам (два способа).
Вопрос 1
Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон без их удвоенного произведения на угол косинус угла между ними.
Доказательство:
Докажем, что втреугольнике АВС
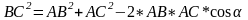
Имеем
векторное равенство
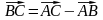 .
Возводя его в квадрат, и проводя некоторые
преобразования, используя теорему о
скалярном произведении векторов, мы
получаем искомый результат.
.
Возводя его в квадрат, и проводя некоторые
преобразования, используя теорему о
скалярном произведении векторов, мы
получаем искомый результат.
Вопрос 2
Первый способ:
Пусть
AB данный отрезок. Описываем окружность
радиусом AB с центром в точках A и B. Пусть
эти окружности пересекаются в точках
С1 и С2.
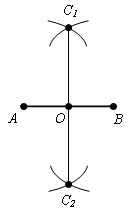 Точки
С1 и С2 лежат в разных полуплоскостях от
прямой AB. Проведем через точки С1 и С2
прямую. Пусть она пересекает прямую AB
в некоторой точке О. Точка О – средина
отрезка AB.
Точки
С1 и С2 лежат в разных полуплоскостях от
прямой AB. Проведем через точки С1 и С2
прямую. Пусть она пересекает прямую AB
в некоторой точке О. Точка О – средина
отрезка AB.
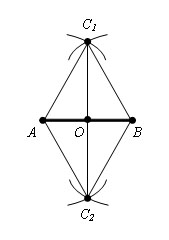 Доказательство.
Δ C1AC2 = Δ C1BC2 по третьему признаку равенства
треугольников (AC1 = BC1, AC2 = BC2, по построению
и С1С2 - общая). Поэтому ∠
AC1C2 = ∠
BC1C2. ОтсюдаследуетΔ
AC1O = Δ
BC1O повторомупризнакуравенстватреугольников
(∠
AC1C2 = ∠
BC1C2, AC1 = BC1 по построению, OC1 – общая).
Следовательно AO = OB и O – середина отрезка
AB.
Доказательство.
Δ C1AC2 = Δ C1BC2 по третьему признаку равенства
треугольников (AC1 = BC1, AC2 = BC2, по построению
и С1С2 - общая). Поэтому ∠
AC1C2 = ∠
BC1C2. ОтсюдаследуетΔ
AC1O = Δ
BC1O повторомупризнакуравенстватреугольников
(∠
AC1C2 = ∠
BC1C2, AC1 = BC1 по построению, OC1 – общая).
Следовательно AO = OB и O – середина отрезка
AB.
Второй способ: Построение Шаг 1. Проведём окружность радиуса AB с центром в точке B. Тем же раствором циркуля отмерим на этой окружности три дуги, начиная от точки A. Получим точку C.
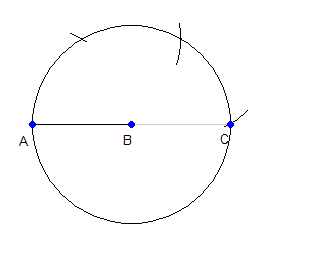
Шаг 2. Проведём окружность радиуса AB с центром в точке A и окружность радиуса AC с центром в точке C. Одну из точек пересечения этих окружностей обозначим D. Шаг 3. Проведём окружность радиуса AB с центром в точке D. Она пересечёт отрезок AB в точках A и E, причём точка E делит отрезок AB пополам.
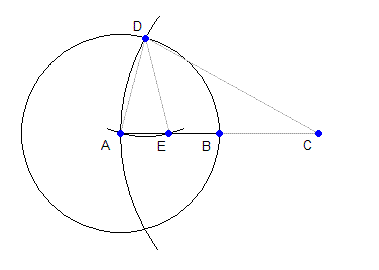
Доказательство Очевидно, что точка C лежит на прямой AB, причём AB=BC, т.е. AC=2*AB По построению треугольники ACD и ADE - равнобедренные, поэтому углы DAE, AED и ADC равны. Отсюда следует, что треугольники ACD и ADE подобны. Запишем отношения сторон: AE/AD = AD/AC, следовательно AE = AD*AD/AC = AB*AB / (2*AB) = AB/2. Доказательство закончено.
Билет №23 1. Теорема о соотношениях между сторонами и углами треугольника. 2. Вертикальные углы (определение). Свойства Вертикальных углов. Смежные углы.