14. Спектры атомов. Боровское представление атома водорода. Правило частот Бора

П остулаты Бора:

1. Электроны в атоме вращаются по строго определенным орбитам без излучения. Такие орбиты называются стационарными и определяются условием

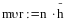
2. Переход с одной стац орбиты на другую соправаждается излучением кванта энергии.

- энергия e находящегося на стационарной орбите.

- радиус стац орбиты

31. Квантовое состояние. Гипотеза де Бройля. Волны де Бройля. Задание состояния движения микрочастицы

Л уи де Бройль перположил, что ЭМ волны можно рассматривать как частицу, но и частицы мргут обладать св-ми волн.

- импульс фотона ф-ла де6 Бройля ( устанавливает зависимость длины волны, связанной с движущейся частицей в-ва от импульса частица р.

Длина волны де Бройля для частицы с массой m, имеющей кинетич энергию Wk

32. Соотношение неопределенностей. Уравнение Шредингера

Соотношениями неопределенностей Гейзенберга называются неравенства: ; ; . В атоме водорода , , отсюда . Момент импульса , поэтому . Энергия E: , r~10^-10 м, E~23·10^-19 Дж~15 эВ. .

Ψ(x,y,z,t) – волновая функция. Плотность вероятности . Условие нормировки .

Волновая функция для реальной волны

Волновое уравнение для описания состояния микрочастицы в пространстве и времени (уравнение Шредингера) - полное уравнение Шредингера – уравнение Шредингера со временем – уравнение для мнимой волны – частицы.

- стационарное уравнение Шредингера. U – потенциальная энергия, Е – полная энергия частицы.

32. Волновая функция. Ее статистический смысл в квантовой механике

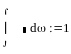-волновая функция (опис вероятностью), - плотность вероятности, - условие нормирования

В случае, когда функция U не зависит от времени dU/dt = 0, ψ(x,y,z) J удовлетворяет стационарному уравнению Шредингера: - стационарное уравнение Шредингера. U – потенциальная энергия, Е – полная энергия частицы.

- оператор Лапласа.

32. Частица в одномерной потенциальной яме

Пусть имеется некая микрочастица, которая находится в пределах одномерного пространства (0,ℓ), а потенциальная энергия U=0 при 0≤x≤ℓ, а при x≤0 и x≥ℓ U=∞.

Такая система называется потенциальной ямой с бесконечно высокими стенками.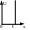 , ψ(0)=0, ψ(ℓ)=0 – частица в положении при х=0 и x=ℓ находится не может. Тогда решение уравнения: , где . => α=0; => =π·n, n=1, 2, 3…

Итак , =π²·n², , отсюда , где n – целое число => энергия может принимать только ряд каких либо значений кратных n, т.е. квантуется.

Из условия нормировки. Условие нормировки => . Значит, волновая функция имеет вид: 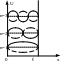n – показывает кратность энергии. n – главное квантовое число.

32. Квазиклассическое приближение. Прохождение частицы под барьером. Туннельный эффект

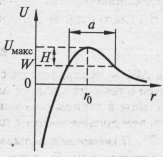
Е сли потенц энергия имеет вид U=U(r), рис, то для перехода частицы из обл. 1 (r<r0) в 2 (r>r0) или обратно частице с энергией W, удовл условию 0<W<Umax, нужно преодолеть потенциальный барьер. H=Umax-W – высота барьера, а его ширина a зависят от W. В квант механике есть отличная от 0 вероятность D (прозрачность) того, что частица, энергия которой W<Umax, может пройти сквозь потенц борьер. Это явление называется туннельным эффектом.

П розрачность барьера для прямоугольного ПБ высотой U0 и шириной L . Для ПБ сложной формы