14. Эффект Доплера.

Эффектом Доплера называется изменение частоты волн регистрируемых приемеником которое происходит в следствии движения источника этих волн и приемника. Например, при приближении к неподвижному наблюдате­лю быстро движущегося поезда тон звукового сигнала последнего выше, а при удалении поез­да - ниже тона сигнала, подавае­мого тем же поездом, когда он стоит на станции. 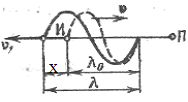Пусть приемник П звуковых волн в газообразной (или жидкой) среде неподвижен относительно нее, а источник И удаляется от приемника со скоростью υ₁ вдоль соединяющей их прямой. X= υ₁·T, – длина волны, где Т₀ – период его колебаний источника, ν₀ — частота коле­баний источника. υ — фазовая скорость волны в среде, Частота волны, регистри­руемая приемником, . При одновременном движении источника и приемника регистрируемая частота будет равна 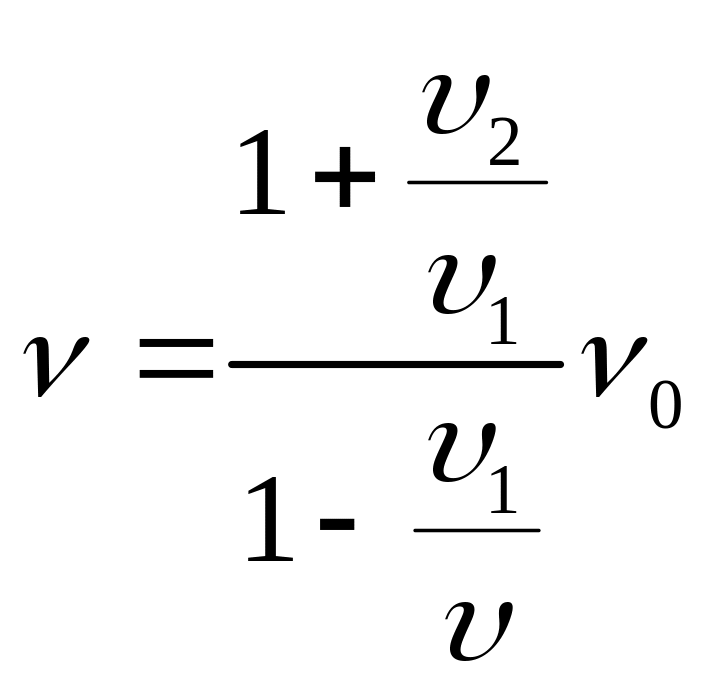, где υ₁ – скорость источника, υ₂ – скорость приемника, ν₀ – частота источника, ν – частота принимаемая приемником.

14. Продольные волны в твердом теле. Энергетические соотношения. Вектор Умова.

Поперечными называются волны, у которых направление колебаний перпендикулярно направлению распространения.

Продольными называются волны, у которых направление распространения совпадает с направлением колебаний.

В твердых телах – продольные и поперечные, а в жидкостях и газах – только продольные.

Пусть в некоторой твердой упругой среде распространили плоскую продольную волну.

мы можем найти величину деформации: , согласно закону Гука и учета модуля юнга: . Пусть эта дифформация имеет единичную площадку, тогда согласно основному поступательному движению: F=m·a, m=ρV= ρS₀∆x= ρ·∆x, тогда , S – функция перемещения волны. F=F_x+∆x-F_x, σ=F/S₀; ; . Итак , , тогда - скорость распространения продольной волны в твердом теле. , где σ – модуль сдвига.

Выделим в упругой среде, где распространияется плоская волна малый объем, в котором скорость движения и деформация будут одинаковы. , , . ∆W=∆W_П+∆W_K; , E=ρυ² – модуль Юнга. - потенциальная энергия. , ; , уравнение волны S=a·sin(ω·t-k·x), , , тогда , , Единица объема волны прямопропорциональна квадрату амплитуды и частоты.

Энергия переносимая через некоторую площадку в единицу времени равна . Энергия переносимая в единицу времени

- вектор Умова показывает поток энергии . .

Интенсивностью волны называется среднее значение вектора Умова . , J~A².

14. Волны в газах и жидкостях.

Если частота волны небольшая, то сжатие будет близко к изотермическому, тогда скорость распространения продольной волны в газе.

- изотермическое сжатие - адиабатическое сжатие. В жидкости

14. Электромагнитные волны. Вектор Пойнтинга

Электромагнитные волны н-возмущения электромагнитного поля (т, е. переменное электромагнитное поле), распространяющиеся в пространстве. Утверждение о существова­нии электромагнитных волн является непосредственным следствием уравнений Максвелла. Для электромагнитного поля вдали от порождающих его свободных электрических зарядов и макроскопических токов эти уравнения имеют вид: , , ,

При распространении волны в одном направлении ,

Энергия электромагнитного поля ,

Плотность энергии , , .

Если , то , тогда , отсюда , , - вектор Пойнтинга. Вектор плотности потока энергии электромаг­нитной волны называется вектором Пойнтинга. Вектор Пойнтинга связывает электрические и магнитные возмущения. [E]=В/м; [H]=А/м; [П]=В·А/м².