41.Распределение 2. (“хи-квадрат”).

Пусть Z_i ~N(0;1) , i=1,2…k, тогда 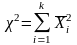–называется СВ распределенной по закону ² с k степенями свободны.

, .

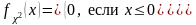
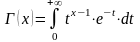
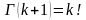
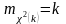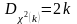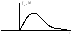
Распределение ² определяется одним параметром числом степеней свободы. С увеличением степеней свободы распределение ² медленно приближается к нормальному. На практике при k > 30 считают, что 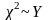, где 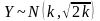.Для СВ, имеющей ² распределение существуют таблицы квантилей.

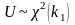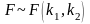
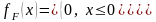
43. Распределение Фишера.Если U и V независимые СВ, распределенные по закону ², , , тогда имеет распределение, которое называется F–распределением или распределением Фишера со степенями свободы k₁ и k₂. ( 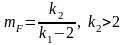F–распределение определяется двумя параметрами k₁ и k₂ и существует таблица квантилей. .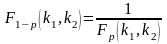

44. Неравенства Чебышева. Следующие два неравенства называют неравенствами Чебышева. Сформулируем их в виде теорем. Теорема: x>0 имеют место неравенства: .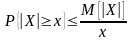

Доказательство:

Разложим X в сумму двух слагаемых

,

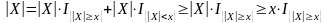
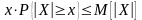так как x > 0, получаем

.

.

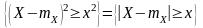
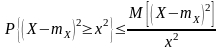
Замечание. Очень часто второе неравенство Чебышева дают в такой форме

.

Второе неравенство Чебышева показывает, что при малой дисперсии с вероятностью близкой к 1 СВ Х концентрируется около своего МО.

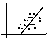
48.Статистическое описание и вычисление оценок параметров распределения системы двух СВ. Пусть исход некоторого эксперимента описывается двумя СВ (X; Y).Предварительное представление о зависимости между X и Y можно получить, нанося элементы двумерной выборки (x_i , y_i ) , i=1,..,n, в виде точек на плоскость с выбранной системой координат. Такое представление называется диаграммой рассеяния.

Опр. Распределением двумерной выборки называется распределение двумерного дискретного СВ случайного вектора, принимающего значения (x_i,, y_i) с вероятностями 1/n. Выборочные числовые характеристики вычисляются как соответствующие числовые характеристики двумерного дискретного случайного вектора. Если объем выборки небольшой, то тогда вычисления проводятся в следующей последовательности:

1. .

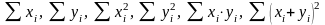Контроль .

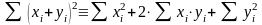2. Суммы квадратов отклонений от среднего и произведения отклонений от среднего

.

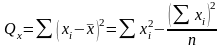
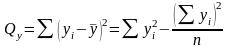
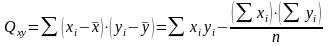3. ; ; .

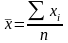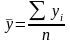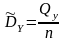
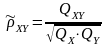49. Линии регрессии Для СВ X и Y.

Регрессией Y на X называется условное МО .

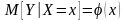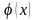используется для предсказания значения СВ Y по фиксированному значению СВ X.

Если 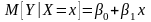, то говорят о линейной регрессии Y на X.

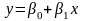– прямая регрессии.

Оценки параметров линейной регрессии по выборке (x_i , y_i ) , i=1,..,n можно получить, используя МНК из условия минимума суммы

.

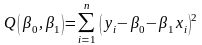–выборочные коэффициенты регрессии.

; .

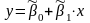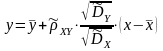Выборочная линейная регрессия Y на X. Аналогично рассматривается X на Y.

; ;

.

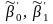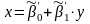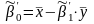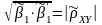
Обе прямые регрессий пересекаются в точке с координатами 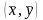. Угол между этими двумя прямыми уменьшается при увеличении коэффициента корреляции. При обе прямые совпадают. Замечание Прямые и должны быть различны.

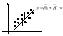
52. Интервальные оценки. Доверительный интервал. Доверительная вероятность.

В ряде задач требуется не только найти для параметра 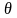подходящую оценку , но и указать к каким ошибкам может привести замена параметра его оценкой , т.е. требуется оценить точность и надежность оценки.

Для определения точности оценки в статистике пользуются доверительными интервалами.

Для определения надежности оценки в статистике пользуются доверительной вероятностью.

Опр. Доверительным интервалом для параметра называется интервал 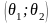, содержащий истинное значение параметра с заданной вероятностью .

.

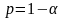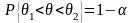Опр. Число называется доверительной вероятностью, а значение  – уровнем значимости.

Замечание. Нижняя 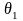и верхняя 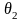граница доверительного интервала определяется по результатам наблюдений и следовательно является СВ. Поэтому так и говорят, что доверительный интервал «накрывает» оцениваемый параметр с вероятностью .

Выбор доверительной вероятности каждый раз определяется конкретной постановкой задачи. Обычно р = 0,9; р = 0,95; р = 0,99.

Часто применяют односторонние доверительные интервалы

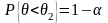(левосторонний), 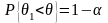(правосторонний).

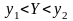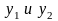В простейших случаях метод построения доверительных интервалов состоит в следующем –оценка , . Предположим, что существует непрерывная и монотонная функция Y, зависящая от и , но такая, что ее распределение не зависит от и других параметров. Для нахождения границ доверительного интервала по заданной доверительной вероятности . В этом случае можно использовать неравенство , где числа , определяются из условия

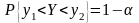
Рассмотрим нахождение доверительного интервала для среднего и дисперсии нормально распределенной генеральной совокупности.