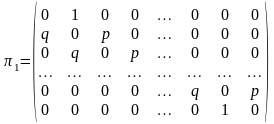55.Доверительный интервал для оценки дисперсии при неизвестном мо.

3) Доверительный интервал для оценки дисперсии при неизвестном МО нормально распределенной генеральной совокупности. Пусть – выборочный вектор n–наблюдений СВ . В этом случае в качестве оценки дисперсии используют .

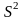В литературе по математической статистике доказано, что 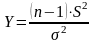имеет распределение .

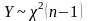По таблице распределения 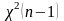определяются квантил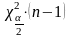и и .

.

.

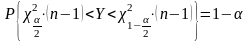
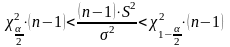
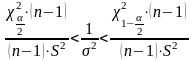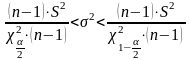58. Марковская зависимость испытаний.

Определение цепи Маркова.

Непосредственным обобщением схемы независимых испытаний является схема цепей Маркова.

Пусть производится последовательность испытаний, в каждом из которых может осуществляться одно и только одно из k несовместных событий.

верхние индексы обозначают номер испытания.

Опр. Последовательность испытаний образует простую цепь Маркова, если условная вероятность в испытании, где S=1,2,3,K осуществится событию , зависит только от того, какое событие произошло при S-ом испытании и не изменяется от добавочных сведений о том, какие события происходили в более ранних испытаниях. Замечание. Часто при изложении теории цепей Маркова придерживаются иной терминологии и говорят о некоторой физической системе S, которая в каждый момент времени может находиться в одном из состояний A₁ ,A₂ ,K,A_k и меняет свое состояние только в моменты t₁ ,t₂ ,K,t_n ,K . 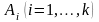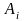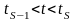Для цепей Маркова вероятность перейти в какое-либо состояние , в момент времени t_S зависит только от самого и того, в каком состоянии система находилась в момент времени и не изменяется оттого, что становятся известными ее состояния в более ранние моменты времени.

Пример 1. В модели Бора атома водорода, электрон может находиться на одной из допустимых орбит. Обозначим, через – электрон находится на i орбите и предположим, что изменение состояние атома может наступать только в моменты (в действительности эти моменты представляют собой СВ), то тогда вероятности перехода с i орбиты на j орбиту в момент времени t_S зависит только от i и j и не зависит от того на каких орбитах находился электрон в «прошлом».

Разность (i–j) зависит от количества энергии, на которую изменился заряд атома в момент времени t_S.

Это пример цепи Маркова с бесконечным числом состояний.

59. Переходные вероятности.

Матрица перехода. Далее будем рассматривать только однородные цепи Маркова, в которых условная вероятность появления события 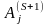при условии, что в предыдущем S-ом испытании осуществилось 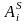не зависит от номера испытания.

Назовем эту вероятность – вероятностью перехода и обозначим .

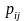Полную вероятностную картину возможных изменений, осуществляющихся при переходе от одного испытания к следующему можно задать с помощью матрицы

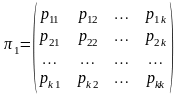– матрица перехода

Замечание.

1. Очевидно, что .

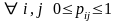2. Из того, что при переходе из состояния 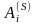система обязательно переходит в одно из состояний , следовательно, в матрице перехода .

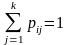Опр. Любая квадратная матрица, элементы которой удовлетворяют следующим требованиям:

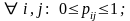
, называется стохастической.

Одной из главных задач в теории цепей Маркова является задача определения вероятности перехода .

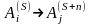
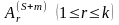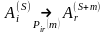Рассмотрим какое-нибудь промежуточное испытание с номером (S+m). В этом испытании осуществится какое-либо одно из возможных событий , тогда вероятность перехода , а вероятность перехода .

По формуле полной вероятности получим

(*)

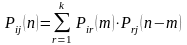Обозначим через

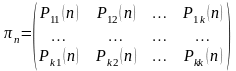
Согласно формуле (*) получаем, что .

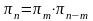
В частности, когда n = 2, получаем

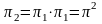
n = 3

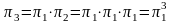
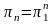
Отметим частный случай формулы (*), когда m = 1

.

Пример 2 Процесс блуждания с отражением.

Пусть частица, находящаяся на прямой, движется по этой прямой под влиянием случайных толчков, происходящих в моменты времени Частица может находиться в точках с целочисленными координатами . В точках a, b находятся отражающие стенки, каждый толчок перемещает частицу вправо с вероятностью p, а влево с вероятностью q, если только частица не находится у стенки. Если частица находится у стенки, то любой толчок переводит ее на 1 внутрь промежутка между стенками.

Получается цепь Маркова с конечным числом состояний.