Лекция № 2. Функции комплексной переменной.

Вопрос 2.1. Гармонические и аналитические функции.

Вопрос 2.2. Геометрический смысл модуля и аргумента производной аналитической функции.

Вопрос 2.3. Конформные отображения.

Вопрос 2.4. Интегрирование по комплексной переменной. Регулярность первообразной.

Лекция № 3. Функции комплексной переменной.

Вопрос 3.1. Теорема Коши. Интегральная формула Коши.

Вопрос 3.2. Формулы для производных. Теорема Морера.

Вопрос 3.3. Функциональные последовательности и ряды. Степенные ряды.

Вопрос 3.4. Ряды Тейлора.

Начнем с обобщения на функции комплексного переменного формулы Тейлора. С ее помощью докажем, что всякая однозначная аналитическая в точке функция представляется в окрестности этой точки в виде суммы ряда Тейлора с центром в точке

.

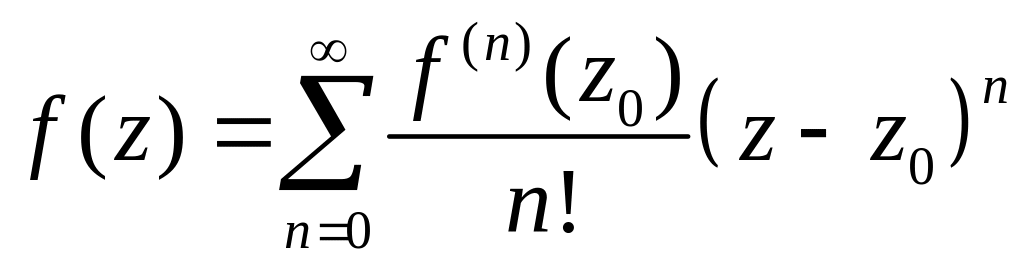Пусть q некоторое комплексное число, тогда воспользуемся формулой суммы конечной арифметической прогрессии

,

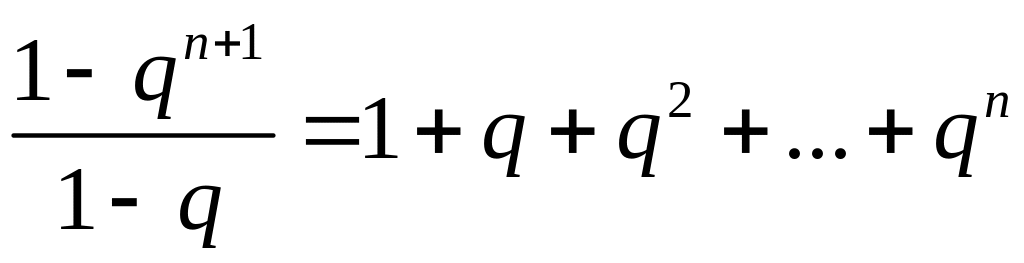переписав ее в виде

,

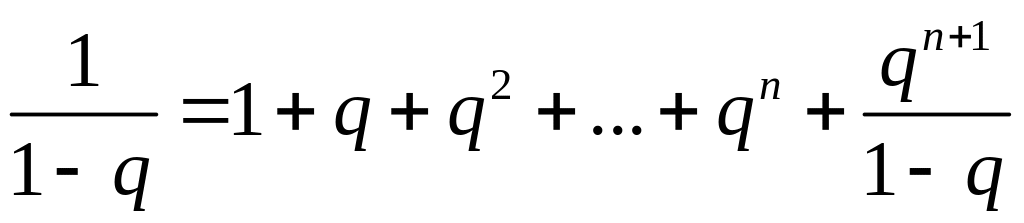для преобразования функции

.

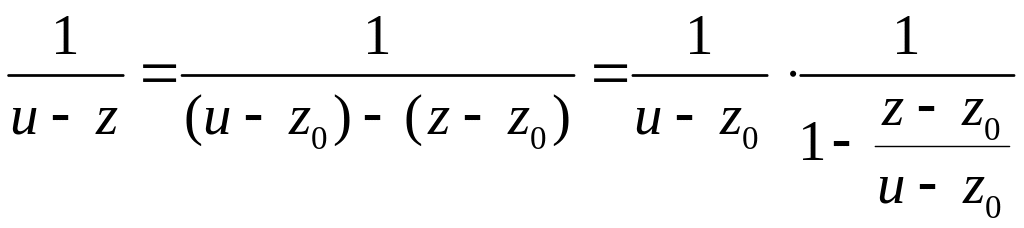Положив 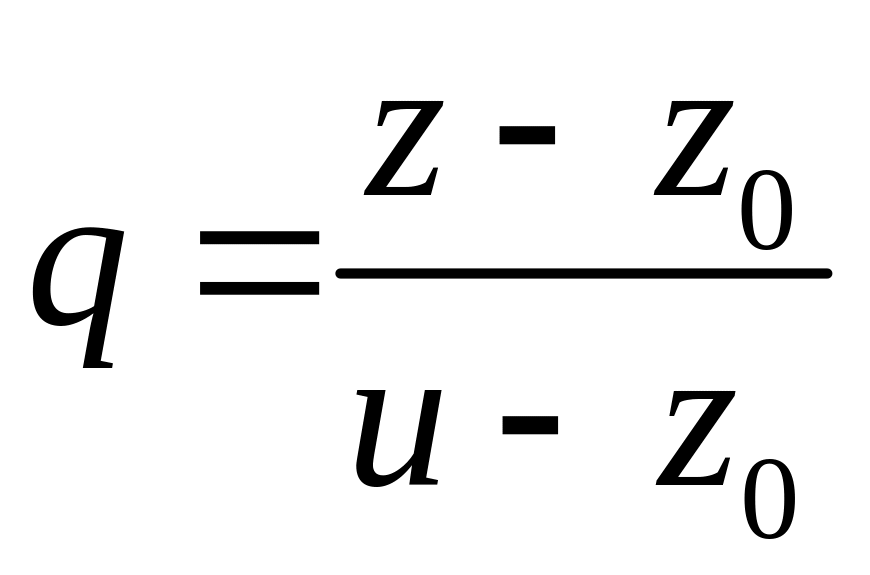, находим

.

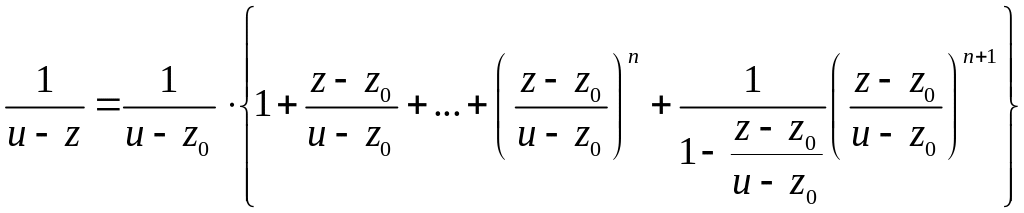Умножим теперь обе части этого равенства на множитель и проинтегрируем его по u вдоль некоторого замкнутого кусочно-гладкого контура С, целиком лежащего в области D и содержащего внутри себя точки z и , обходя его один раз против часовой стрелки. Тогда получим

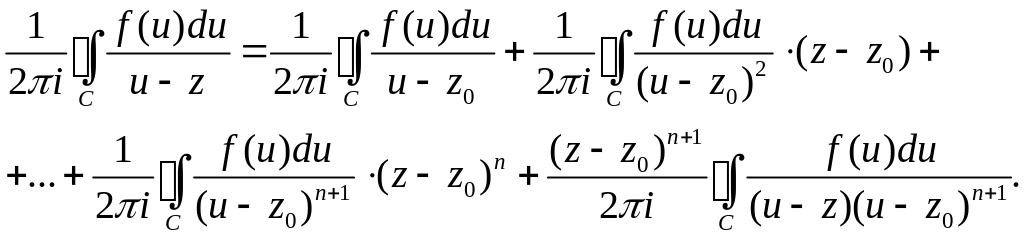
Применяя формулу Коши и формулы для высших производных

,

,

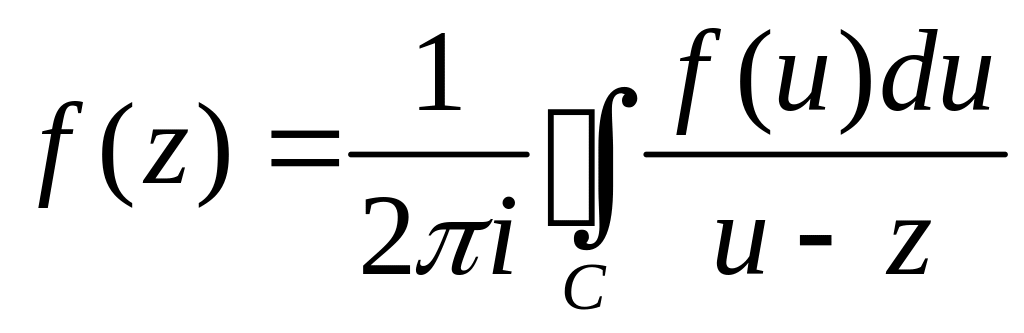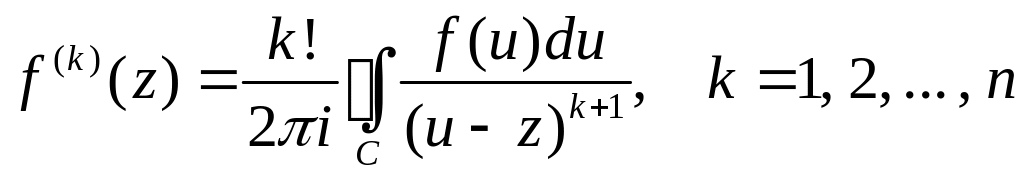получим формулу Тейлора n-го порядка

где остаточный член имеет вид

.

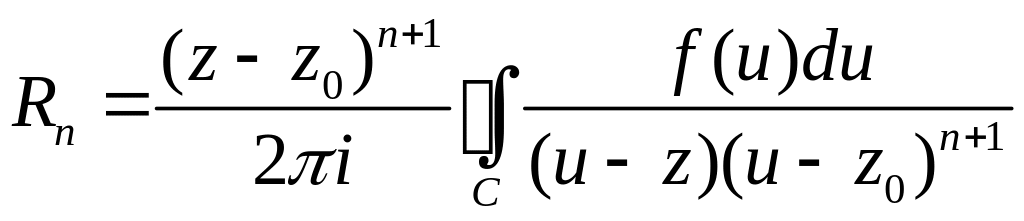Пусть однозначная аналитическая функция задана на области D и пусть внутренняя точка этой области. Тогда всегда найдется некоторый открытый круг с центром в точке и радиусом R, целиком принадлежащий области D ( ). Обозначим границу окружность

Вопрос 3.5. Ряды Лорана. Лекция № 4. Функции комплексной переменной.

Вопрос 4.1. Изолированные особые точки, их классификация.

Вопрос 4.2. Вычеты, их вычисление.

Вопрос 4.3. Основная теорема о вычетах.

Пусть однозначная аналитическая функция определена на области D, и содержит внутри области D конечное число изолированных особых точек . Пусть в области D задан простой замкнутый контур Г (т.е. замкнутая, без точек самопересечения, кусочно-гладкая кривая), содержащий внутри себя все особые точки (см. рис. 4.1). И пусть простой замкнутый контур обходится в положительном направлении (т.е. против часов часовой стрелки) один раз. Тогда справедлива теорема:

Теорема 4.1. (Основная теорема Коши о вычетах). Интеграл от функции , взятый по замкнутому простому контуру Г, проходимому в положительном направлении один раз, содержащемуся в области D, где функция является однозначной и аналитической, за исключением конечного числа изолированных особых точек, и не проходящему через особые точки, равен умноженной на сумме вычетов функции относительно всех особых точек, заключенных внутри контура Г:

.

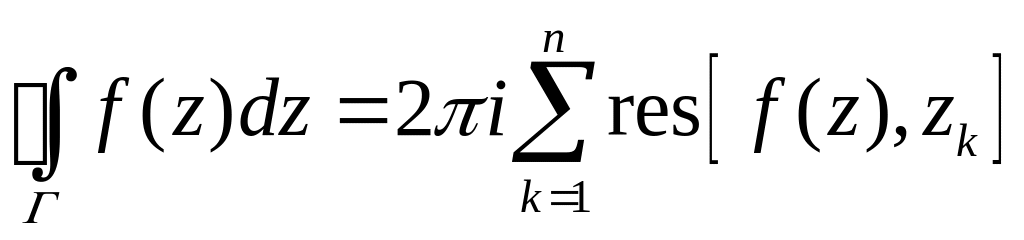Доказательство.

Конец доказательство.

Вопрос 4.4. Применение вычетов к вычислению интегралов. Лекция № 5. Операционное исчисление.

Вопрос 5.1. Преобразование Лапласа, его свойства. Оригинал и изображение.

Вопрос 5.2. Основные теоремы операционного исчисления.