Вопрос 1. Элементы математической статистики. Выборка и ее представление.

Математическая статистика изучает методы и способы обработки результатов наблюдений массовых явлений и их анализ. Теоретической основой математической статистики является теория вероятностей.

Задачи математической статистики можно разбить на три класса:

1) обработка массовых результатов наблюдений

2) проверка гипотез

3) оценка параметров законов распределений.

ОПРЕДЕЛЕНИЕ 1. Множество значений, которые может принимать случайная величина X называется генеральной совокупностью.

ОПРЕДЕЛЕНИЕ 2. Выборкой случайной величины X объема n называется n ее значений , полученных в результате n независимых измерений. Эти значения называются элементами выборки.

Таким образом выборка получается из генеральной совокупности путем регистрации значений случайной величины. Выборку можно представить разными способами: в виде вариационного и статистического ряда.

ОПРЕДЕЛЕНИЕ 3. Вариационным рядом называется выборка объема n, в которой элементы выборки расположены в порядке возрастания, то есть .

Если объем выборки велик, то вариационный ряд не очень удобен как форма представления выборки.

ОПРЕДЕЛЕНИЕ 4. Статистическим рядом называется выборка объема n записанная в виде таблицы

				...
				...

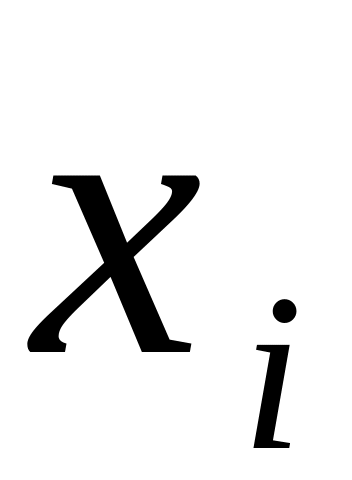
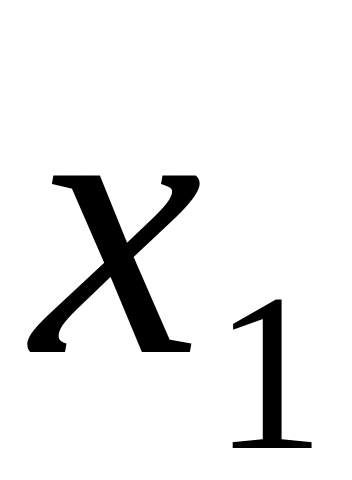
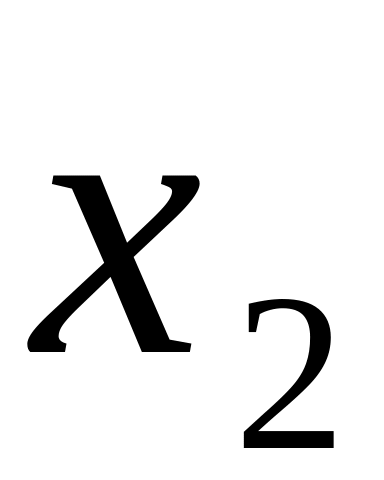
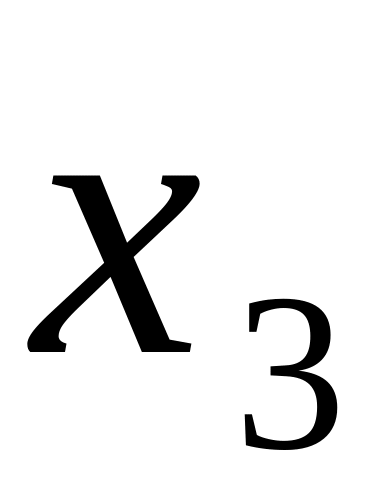
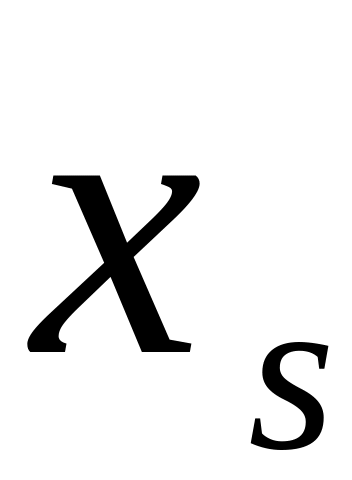
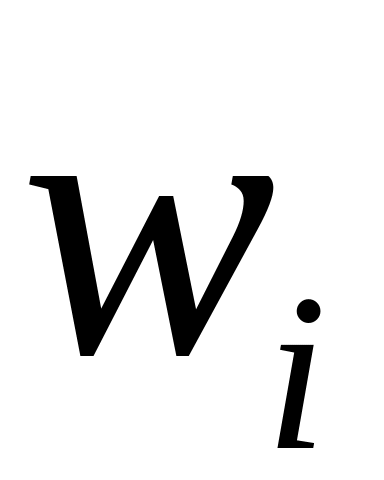
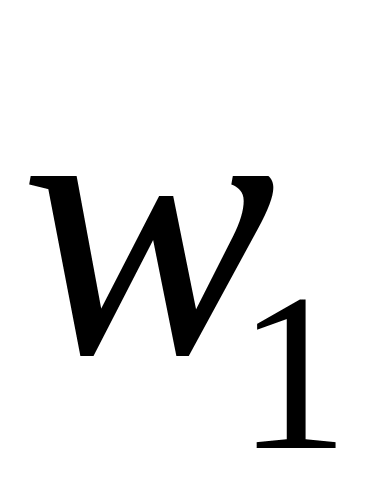
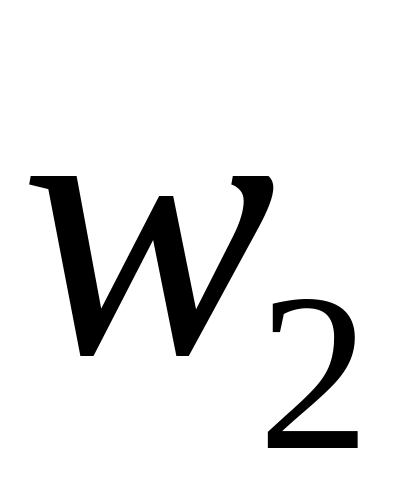
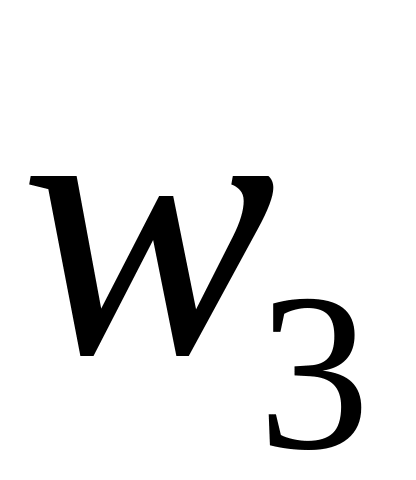
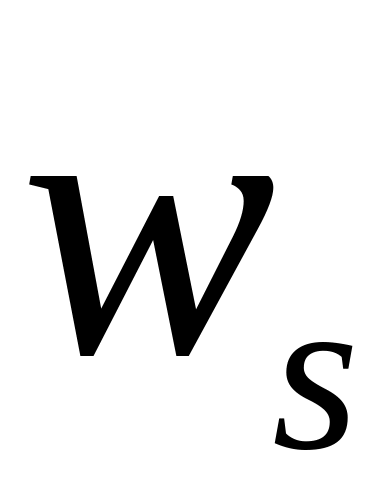
где - различные по величине элементы, а их частоты ( есть число повторений элемента в выборке). Очевидно, что сумма всех частот должна равняться объему выборки.

ПРИМЕР 1. Пусть дана выборка 3, 4, 2, 2, 4, 5, 7, 3, 5, 4, 3 объема n=11. Требуется представить ее в виде вариационного и статистического ряда.

Вариационный ряд имеет вид 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 7

Статистический ряд

	2	3	4	5	7
	2	3	3	2	1

Сумма всех частот равна 2+3+3+2+1=11

КОНЕЦ ПРИМЕРА.

Статистический ряд можно представить и как ряд относительных частот, если подставить их во вторую строку таблицы.

				...
				...

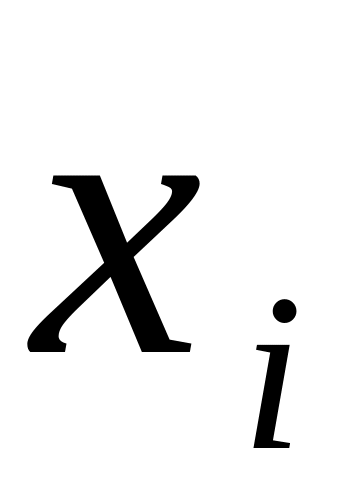
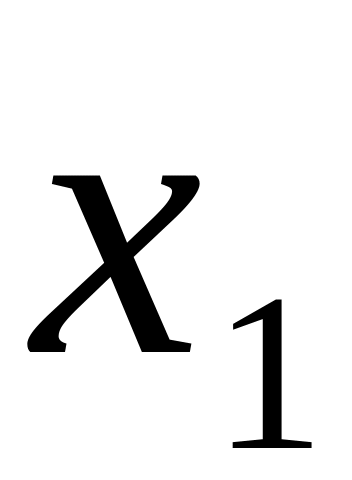
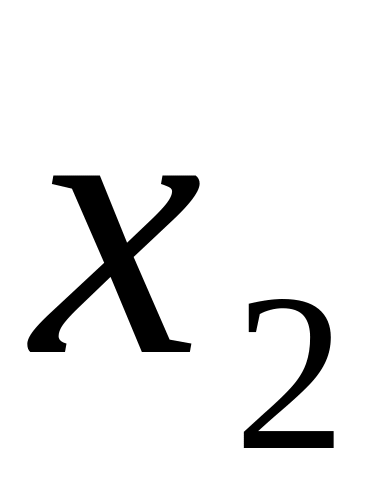
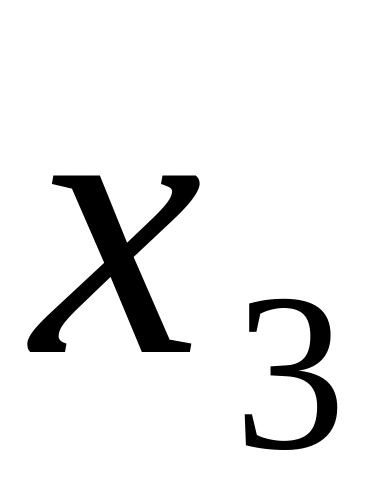
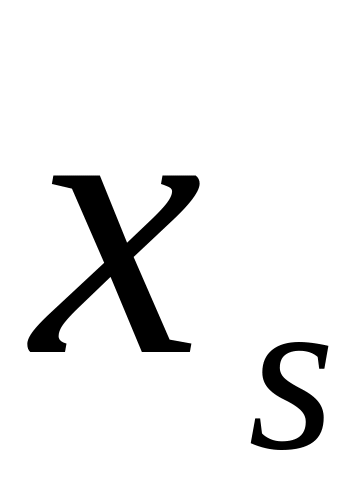
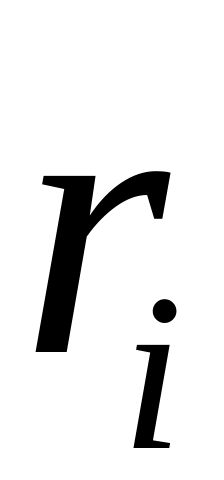
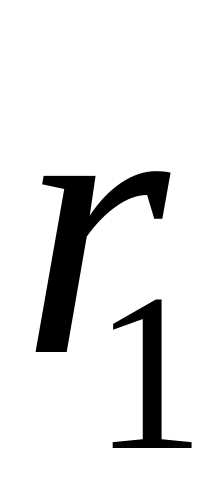
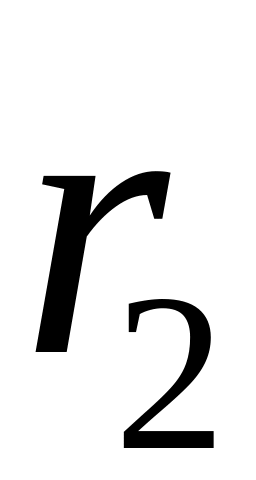
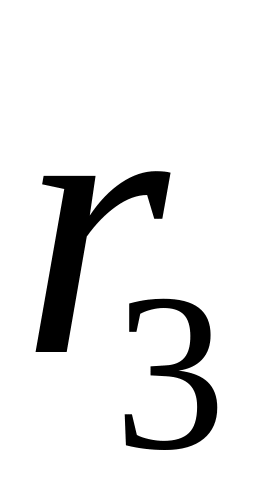
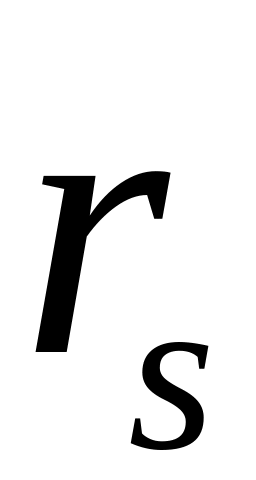
где . В этом случае нужно указывать объем выборки. Очевидно, что сумма всех относительных частот теперь равна 1.

ПРИМЕР 2. Представить статистический ряд из примера 1 в виде статистического ряда по частотам.

Статистический ряд

	2	3	4	5	7
	2/11	3/11	3/11	2/11	1/11

n=11.

Сумма всех частот равна 1.

КОНЕЦ ПРИМЕРА.

Выборку можно представить графически в виде группированного статистического ряда. Для этого определяют максимальный и минимальный элемент выборки и разбивают интервал на некоторое число интервалов группировки. Количество этих интервалов обычно берут в пределах от 5 до 20. Длины этих интервалов обычно равны, хотя это необязательно. Далее подсчитывают количество элементов попавших в первый интервал , во-второй и т.д.. Если обозначить интервалы через , и т.д., то получаем группированный статистический ряд

				...
				...

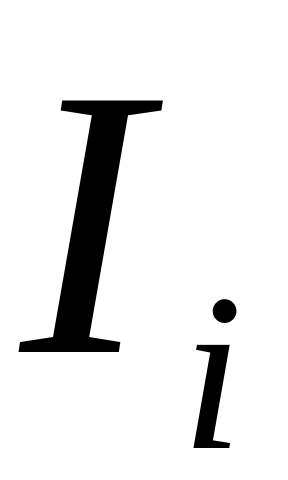
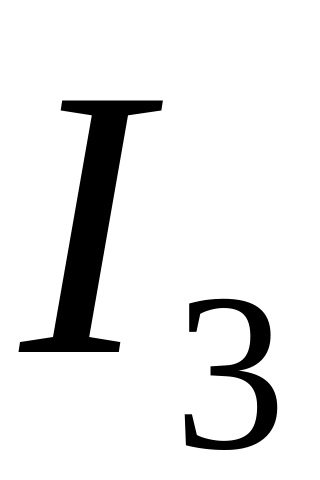
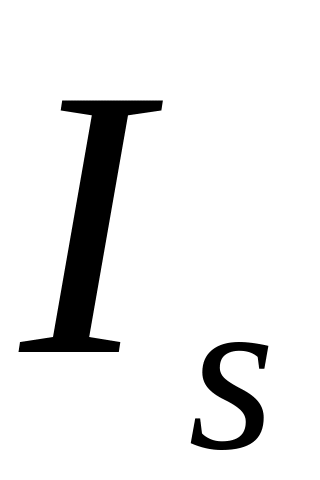
Вместо частот можно использовать число элементов, деленное на объем выборки n. Группированный статистический ряд можно представить графически в виде гистограммы или полигона. Гистограмма представляет из себя плоскую фигуру, составленную из прямоугольных треугольников. Основанием прямоугольника является интервал группировки , а высота равна . Полигон представляет из себя ломаную, вершины которой имеют абсциссу равную середине интервала группировки, а ординату равную частоте или относительной частоте. В математической статистике показано, что с ростом объема выборки до бесконечности полигон или гистограмма все лучше и лучше приближаются к графику функции распределения вероятности. Таким образом, график этой функции можно восстановить приближенно по результатам измерений.