Вопрос 2. Функция распределения вероятностей.

Из определения случайной величины следует, что для любого вещественного x определена вероятность события . Рассмотрим свойства функции распределения:

1) (событие является достоверным)

2) (событие является невозможным

3) (простое следствие )

4) Если , то (следует из того факта, что

5) (непрерывность слева, будем записывать это так )

Рассмотрим теперь, как вероятности некоторых событий, связанных со случайными величинами, выражаются через функцию распределения случайной величины X.

ТЕОРЕМА 2. Пусть X некоторая случайная величина и ее функция распределения вероятностей. Тогда справедливы равенства

1)

2)

3)

4)

5)

6)

7)

8)

ДОКАЗАТЕЛЬСТВО. Равенство 1) следует из определения функции распределения. Равенства 2) вытекает из простого факта или . Равенство 3) следует из соотношения , которое можно записать в виде . Соотношения 7) и 8) выводятся аналогично.

КОНЕЦ ДОКАЗАТЕЛЬСТВА.

Вопрос 3. Классификация случайных величин. Числовые характеристики случайных величин.

Случайные величины можно разделить на три класса: дискретные, непрерывные и сингулярные. Величины последнего типа, то есть сингулярные, в широкой инженерной практике не встречаются и в дальнейшем рассматриваться не будут.

ОПРЕДЕЛЕНИЕ 3. Дискретной случайной величиной X называется случайная величина, принимающая счетное число значений . с вероятностями . Так как события несовместны (это элементарные исходы), то сумма их вероятностей равна 1, то есть .

Для дискретной случайной величины функция распределения вероятностей имеет вид . Эта формула непосредственно следует из определения. Отсюда нетрудно получить формулу .

ОПРЕДЕЛЕНИЕ 4. Непрерывной случайной величиной X непрерывного типа называется случайная величина, функция распределения которой имеет вид

где p(t) - кусочно-непрерывная функция, называемая плотностью распределения вероятностей.

Из определения следуют следующие свойства плотности распределения вероятности непрерывной случайной величины :

1) (условие нормировки, оно является простым следствием соотношения )

2) непрерывна на всей вещественной оси X. Отсюда несложно доказать, что для непрерывных случайных величин

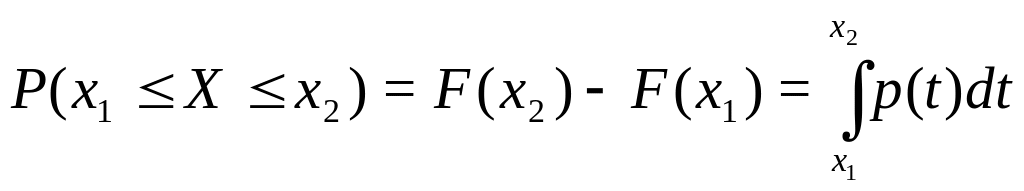
3) в точках непрерывности p(x).

Рассмотрим теперь числовые характеристики случайных величин- математическое ожидание дисперсию.

ОПРЕДЕЛЕНИЕ 5. Математическим ожиданием (средним значением) случайной величины X называется число

если случайная величина является дискретной или

если случайная величина является непрерывной.

В случае дискретной случайной величины нетрудно определить смысл математического ожидания. Для этого предположим, что в N измерениях случайная величина принимала значения раз, раза, ... , раз. Тогда среднее арифметическое результатов измерений равно

при

ОПРЕДЕЛЕНИЕ 6. Дисперсией случайной величины X называется число

если случайная величина является дискретной или

если случайная величина является непрерывной. Дисперсия характеризует разброс случайной величины около ее среднего значения.

Л Е К Ц И Я N 16