Области применения

• Детекторы пересечения нуля

• Детекторы перенапряжений

• Широтно-импульсные модуляторы

• Прецизионные выпрямители

• Аналого-цифровые преобразователи

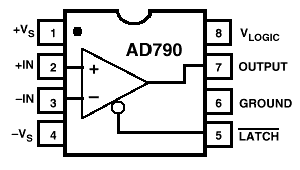
Цоколевка (вид сверху)

Назначение выводов: +IN - неинвертирующий вход -IN - инвертирующий вход +V - положительное напряжение питания -V - отрицательное напряжение питания OUT - выход BAL - балансировочные входы GND - общий +VL - напряжение питания выходной логики

Технические характеристики аналогового компаратора AD790

• Время задержки распространения не более 45 нс

• Работа от одного +5 В или двух +/-15 В источников

• ТТЛ и КМОП совместимый выход

• Смещение нуля не более 250 мкВ

• Гистерезис переходной характеристики не более 500 мкВ

• Допустимо входное дифференциальное напряжение до 15 В

• Внутренняя защелка выхода

• Мощность потребления 60 мВт

• Выпускается в 8-выводных пластиковом и керамическом DIP-корпусах и в 8-выводном SOIC

Области применения

• Детекторы пересечения нуля

• Детекторы перенапряжений

• Широтно-импульсные модуляторы

• Прецизионные выпрямители

• Аналого-цифровые преобразователи

• Дельта-сигма модуляторы для АЦП

Цоколевка (вид сверху)

DIP	SOIC
Назначение выводов: +IN - неинвертирующий вход -IN - инвертирующий вход +VS - положительное напряжение питания -VS - отрицательное напряжение питания OUTPUT - выход VLOGIC - напряжение питания логического выхода GROUND - общий LATCH - вывод управления защелкой

Технические характеристики аналогового компаратора СМР-02

• Смещение нуля не более 0,8 мВ

• Входной ток не более 50 нА

• Разность входных токов не более 3 нА

• Температурный дрейф смещения нуля 1 мкВ/°С, 4 пА//°С

• Коэффициент усиления не менее 200 000

• Коэффициент ослабления синфазного сигнала не менее 94 дБ

• Входное сопротивление не менее 16 МОм

• Задержка распространения не более 270 нс

• Питание +5 или +/-5…+/-18 В

• ТТЛ совместимый выход

• Выпускается в 8-выводных пластиковом DIP-корпусе и металлическом ТО-99

Области применения

• Детекторы пересечения нуля

• Детекторы перенапряжений

• Широтно-импульсные модуляторы

• Прецизионные выпрямители

• Аналого-цифровые преобразователи

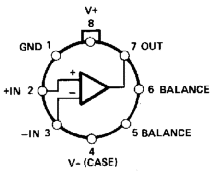
Цоколевка (вид сверху)

ТО-99	DIP
Назначение выводов: +IN - неинвертирующий вход -IN - инвертирующий вход V+ - положительное напряжение питания V- - отрицательное напряжение питания (корпус ТО-99) OUT - выход BALANCE - балансировочные входы GND - общий

МОДЕЛИРОВАНИЕ МСК-ДАТЧИКА-КОМПAРАТОРА С ТРЕМЯ СТЕПЕНЯМИ СВОБОДЫ.

Кривобоков Д.Е.(аспирант)

АлтГТУ г. Барнаул.

Малый интерес, проявляемый к связанным колебательным системам с тремя и более степенями свободы, объясняется значительными трудностями при математическом моделировании, так чтобы описать поведение системы трёх автогенераторов с двумя элементами связи необходимо решать систему из трёх дифференциальных нелинейных уравнений второй степени. Однако с помощью ряда упрощений можно привести к системе из двух дифференциальных уравнений первого порядка. Упрощения следующие (рисунок 1): крайние автогенераторы заменяются генераторами, т.е. имеют стабильные амплитуды и частоты. При этом, воздействие со стороны генераторов оказывается только на автогенератор.

Рисунок 1Система с тремя степенями свободы, приведённая к двум.

Сиситема дифференциальных уравнений при условии равенства амплитуд колебаний генераторов имеет вид:

; (1)

где А – амплитуда свободных автоколебаний;

А₀ – амплитуда стационарных колебаний автогенератора;

U – амплитуда колебаний генераторов;

 - характеризует степень возбуждения автогенератора АГ;

 - средняя частота собственных колебаний автогенератора;

 - разность фаз между первым генератором Г1 и автогенератором;

1 = ₁- - абсолютная расстройка частот Г1;

2 = ₂- - абсолютная расстройка частоты АГ относительно средней частоты колебаний;

- эквивалентный коэффициент связи;

- разность фаз вносимая вторым генераторов Г2;

_г = ₁-₃ абсолютная расстройка генераторов.

На первый взгляд система, представленная на рисунок 1 соответствует двум ступеням свободы, однако относительно автогенератора АГ реализуется полноценный режим связанных колебаний с тремя степенями свободы. Работа в режиме компаратора предполагает высокую чувствительность. Очевидно, что максимальная чувствительность достигается при работе системы на границе устойчивости. В МСК – датчиках это граница синхронизма. Принимая во внимание что колебательная система работает на границе устойчивости, вид системы (1) значительно упрощается. Так именно в момент синхронизации амплитуда автогенератора АГ достигает нулевого значения в области противофазных колебаний, а так как эта точка является минимумом, то и скорость изменения амплитуды равно нулю. Это очевидно из соображений симметрии системы относительно автогенератора. Так в синхронном режиме синхронизирующий генератор стремиться компенсировать потери в автогенераторе за счёт собственной энергии. На границе синхронизма оба генератора в одинаковой степени воздействуют на АГ, и при противофазных колебаниях происходит полное подавление амплитуды колебаний автогенератора. Ширина области противофазных колебаний быстро стремиться к нулю, и в короткое время (относительно периода биений генераторов) достигает разности фаз 2. При принятых упрощениях решение системы (1)относительно коэффициента связи ₂ имеет вид:

; (2)

Результаты экспериментов хорошо согласуются с (2), причём, как для рассмотренной системы двух генераторов и одного автогенератора, так и для трёх автогенераторов. Это позволяет утверждать о возможности эквивалентной замены параметров сложных систем, и сведение их к более простым видам. Однако, следует отметить, что в данном случае подобное стало возможным лишь благодаря введению третьей степени свободы и выбранному режиму колебаний, которые обеспечивают дифференциальный режим работы системы на границе устойчивости.

Используемые источники информации:

1. В.Н. Седалищев, нелинейные пьезорезонансные датчики. Учебное пособие. АлтГТУ им Ползунова – Барнаул: 1999 – 85 с.