Министерство образования Российской Федерации

Уфимский Государственный Авиационный Технический Университет

Лабораторная работа 4

РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ ДЛЯ ЛИНЕЙНОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ВТОРОГО ПОРЯДКА МЕТОДОМ ПРОГОНКИ

Выполнила студентка

группы ВМ-226 т:

Курамшина А.Р.

Проверил

преподаватель:

Шерыхалина Н.М.

Уфа 2006

1 Краткая теория:

Пусть на отрезке [a,b] требуется найти решение дифференциального уравнения

, (1)

удовлетворяющее следующим краевым условиям:

, , (2)

Численное решение задачи состоит в нахождении приближённых значений y₀, y₁, …, y_n искомого решения y(x) в точках x₀, x₁, …, x_n. Точки x₀, x₁, …, x_n называются узлами сетки. Используем равномерную сетку, образованную системой равноотстоящих узлов i=0, 1, 2, …, n. При этом x₀=a, x_n=b, h=(b-a)/n. Величина h – шаг сетки. Пусть p(x_i)=p_i, q(x_i)=q_i, f(x_i)=f_i, y(x_i)=y_i, y(x_i)=y_i, y(x_i)=y_i. Аппроксимируем y(x_i) и y(x_i) в каждом внутреннем узле центральными разностными производными

и на концах отрезка – односторонними производными

Используя эти формулы, получаем разностную аппроксимацию исходной задачи (1) – (2):

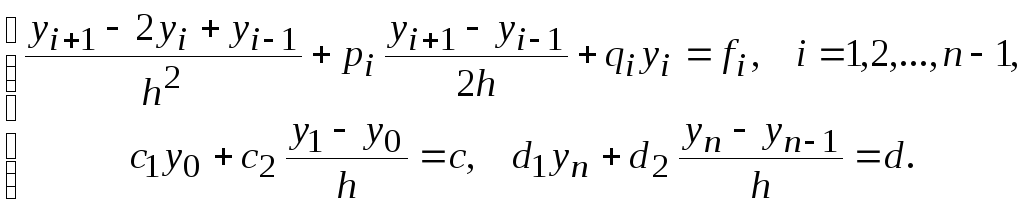(3)

Чтобы найти приближённые значения y₀, y₁, …, y_n искомого решения, необходимо решить систему n+1 линейных уравнений (2) с n+1 неизвестными. Эту систему можно решить одним из стандартных методов решения линейных систем. Однако матрица системы (3) трёхдиагональная, поэтому для её решения применим специальный метод, называемый методом прогонки.

Перепишем систему (3) следующим образом:

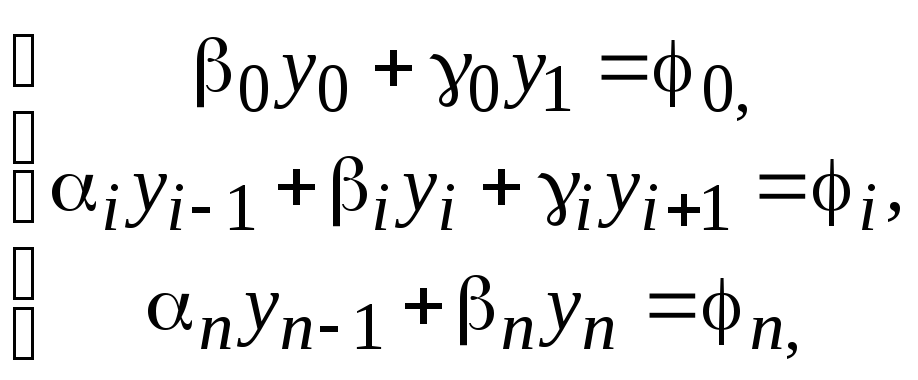
(4)

где b₀=c₁h–c₂, g₀=c₂, j₀=hc, j_i=f_ih², a_i=1–(1/2)p_ih, b_i=q_ih²–2, _i=1+(1/2)p_ih, i=1, 2, …, n–1, a_n=–d₂, b_n=hd₁+d₂, j_n=hd.

Будем искать решение системы (4) в виде

. (5)

тогда для u_i и v_i получаем следующие рекуррентные формулы:

.

Чтобы сделать схему счёта однородной, положим a₀=0, g_n=0. Прямой ход прогонки состоит в последовательном вычислении коэффициентов u_i и v_i, исходя из значений

v₀=–g₀/b₀, u₀=j₀/b₀.

При обратном ходе прогонки по формуле (5) последовательно определяются величины y_n, y_n-1, …, y₀. Так как g_n=0, то v_n=0 и y_n=u_n, т.е. в прямом ходе прогонки вычисляются величины v_n, u_n и приближённое значение решения y_n на правом конце отрезка. Остальные величины y_n-1, y_n-2, …, y₀ вычисляются в обратном ходе прогонки по рекуррентной формуле (5). Таким образом, метод прогонки позволяет найти точное решение системы (3).

Погрешность решения краевой задачи (1)–(2) определяется только погрешностью разностной аппроксимации O(h^k) исходной задачи системой (3). Порядок аппроксимации k равен 2, если с₂=d₂=0, или 1 в противном случае. Так как h=(b-a)/n, то выбирая n достаточно большим, можно добиться уменьшения погрешности ценой увеличения объёма вычислений при решении системы (3).

При практической оценке погрешности найденного решения обычно используют правило Рунге. Если y(x_i) – точное значение решения в узле x_i, а y_i и – приближённые значения решения в том же узле, полученные соответственно с шагом h и h/2, то оценка погрешности решения y_i определяется формулой

, .

Задание:

На отрезке [a,b] решить методом прогонки линейную краевую задачу

Здесь

p(x)	Q(x)	a	b	c	d	a1	a2	b
		0	0,8	-0,5	0,5	2	0	6

_{Листинг программы:}

_{#include <iostream.h>}

_{#include <stdio.h>}

_{#include <math.h>}

_{#include <stdlib.h>}

_{#include <windows.h>}

_{#include <iomanip.h>}

_{void main()}

_{

_{int n,i,k;}

_{float h,c1,c2,c,d1,d2,d,fx,a,b,k1,k2,m,H,runge;}

_{float p[9999],q[9999],betta[9999],gamma[9999],fi[9999],alfa[9999];}

_{float y[9999],u[9999],v[9999],x[9999],Y[9999];}

_c1=d1=1.0;

_c2=d2=1.0;

_fx=0.0;

_{cout<<"Vvedite kraia otrezka [a,b] i 4islo uzlov n"<<endl;}

_{cout<<endl<<"a=";}

_cin>>a;

_{cout<<endl<<"b=";}

_cin>>b;

_{cout<<endl<<"n=";}

_{cin>>n; cout<<endl<<"A tak ge parametri c,d,k1,k2,m"<<endl;}

_{cin>>c>>d>>k1>>k2>>m;}

_x[0]=a;

_h=(b-a)/n;

_{betta[0]=c1*h-c2;}

_gamma[0]=c2;

_fi[0]=h*c;

_alfa[0]=0;

_{for(i=1;i<n;i++)}

_{

_{x[i]=x[i-1]+h;}

_{p[i]=(k1+k2*x[i])/(x[i]*x[i]-1);}

_{q[i]=m/sqrt(1-x[i]*x[i]);}

_{fi[i]=fx*h*h;}

_{alfa[i]=1-(1/2)*p[i];}

_{betta[i]=q[i]*h*h-2;}

_{gamma[i]=1+(1/2)*p[i]*h;}

_}

_alfa[n]=-d2;

_{betta[n]=h*d1+d2;}

_fi[n]=h*d;

_{v[0]=gamma[0]/betta[0];}

_{u[0]=fi[0]/betta[0];}

_{for(i=1;i<n;i++)}

_{

_{v[i]=-gamma[i]/(betta[i]+alfa[i]*v[i-1]);}

_{u[i]=(fi[i]-alfa[i]*u[i-1])/(betta[i]+alfa[i]*v[i-1]);}

_}

_y[n]=u[n];

_{for(i=n-1;i>0;i--)}

_{y[i]=u[i]+v[i]*y[i+1];}

_{cout<<" i"<<" x "<<" y"<<endl;}

_{for(i=0;i<n;i++)}

_{

_{cout.width(4);}

_cout<<i;

_{cout.width(5);}

_cout<<x[i];

_{cout.width(14);}

_{cout<<y[i]<<endl;}

_}

_{H=(b-a)/(2*n);}

_{betta[0]=c1*H-c2;}

_gamma[0]=c2;

_fi[0]=H*c;

_alfa[0]=0;

_k=2*n;

_{for(i=1;i<k;i++)}

_{

_{x[i]=x[i-1]+H;}

_{p[i]=(k1+k2*x[i])/(x[i]*x[i]-1);}

_{q[i]=m/sqrt(1-x[i]*x[i]);}

_{fi[i]=fx*H*H;}

_{alfa[i]=1-(1/2)*p[i];}

_{betta[i]=q[i]*H*H-2;}

_{gamma[i]=1+(1/2)*p[i]*H;}

_}

_alfa[k]=-d2;

_{betta[k]=H*d1+d2;}

_fi[k]=H*d;

_{v[0]=gamma[0]/betta[0];}

_{u[0]=fi[0]/betta[0];}

_{for(i=1;i<k;i++)}

_{

_{v[i]=-gamma[i]/(betta[i]+alfa[i]*v[i-1]);}

_{u[i]=(fi[i]-alfa[i]*u[i-1])/(betta[i]+alfa[i]*v[i-1]);}

_}

_Y[k]=u[k];

_{for(i=2*n-1;i>0;i--)}

_{Y[i]=u[i]+v[i]*Y[i+1];}

_{cout<<" i"<<" x "<<" Y"<<endl;}

_{for(i=0;i<k;i++)}

_{

_{cout.width(4);}

_cout<<i;

_{cout.width(5);}

_cout<<x[i];

_{cout.width(14);}

_{cout<<Y[i]<<endl;}

_}

_{cout<<"pogre6nost' po pravily runge:"<<endl;}

_{for(i=0;i<n;i++)}

_{

_{runge=(Y[2*i]-y[i]);}

_{cout<<runge<<endl;}

_}

_{system("PAUSE");}

_}

_{результаты выполнения программы:}

_{Vvedite kraia otrezka [a,b] i 4islo uzlov n}

_a=0

_b=0.8

_n=10

_{A tak ge parametri c,d,k1,k2,m}

_-0.5

_0.5

₂

₀

₆

_{i x y}

_{0 0 -1.07374e+008}

_{1 0.08 -1.17093e+007}

_{2 0.16 -3.56949e+007}

_{3 0.24 -5.8292e+007}

_{4 0.32 -7.85832e+007}

_{5 0.4 -9.56894e+007}

_{6 0.48 -1.08786e+008}

_{7 0.56 -1.17122e+008}

_{8 0.64 -1.20028e+008}

_{9 0.72 -1.16936e+008}

_{i x Y}

_{0 0 -1.07374e+008}

_{1 0.04 -6.11385e+006}

_{2 0.08 -1.85376e+007}

_{3 0.12 -3.07827e+007}

_{4 0.16 -4.27302e+007}

_{5 0.2 -5.42622e+007}

_{6 0.24 -6.52625e+007}

_{7 0.28 -7.56174e+007}

_{8 0.32 -8.52161e+007}

_{9 0.36 -9.39513e+007}

_{10 0.4 -1.0172e+008}

_{11 0.44 -1.08423e+008}

_{12 0.48 -1.13967e+008}

_{13 0.52 -1.18264e+008}

_{14 0.56 -1.21231e+008}

_{15 0.6 -1.22794e+008}

_{16 0.64 -1.22884e+008}

_{17 0.68 -1.21438e+008}

_{18 0.72 -1.18402e+008}

_{19 0.76 -1.13728e+008}

_{pogre6nost' po pravily runge:}

₀

_{-6.82829e+006}

_{-7.03533e+006}

_{-6.97049e+006}

_{-6.63286e+006}

_{-6.03042e+006}

_{-5.18041e+006}

_{-4.10966e+006}

_{-2.85524e+006}

_{-1.46519e+006}

_{Для продолжения нажмите любую клавишу . . .}