2.4. Лучевой и волновой эллипсоиды Френеля

Как было показано ранее - см. выражение (2.6), - в системе главных диэлектрических осей объемная плотность электрической энергии поля определяется двумя аналогичными выражениями:

.

Введя новые переменные ; ; и ; ; , где , получим уравнения двух эллипсоидов

, (2.21)

, (2.22)

и

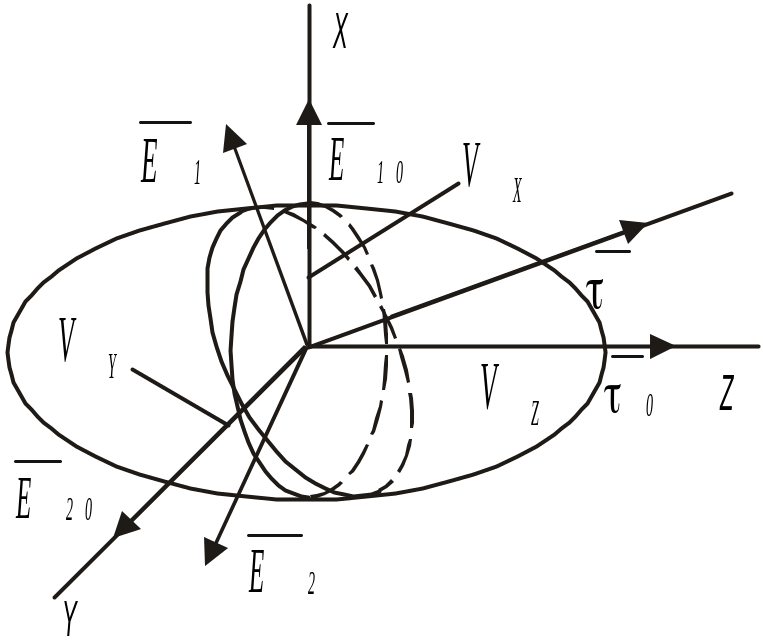Рис. 11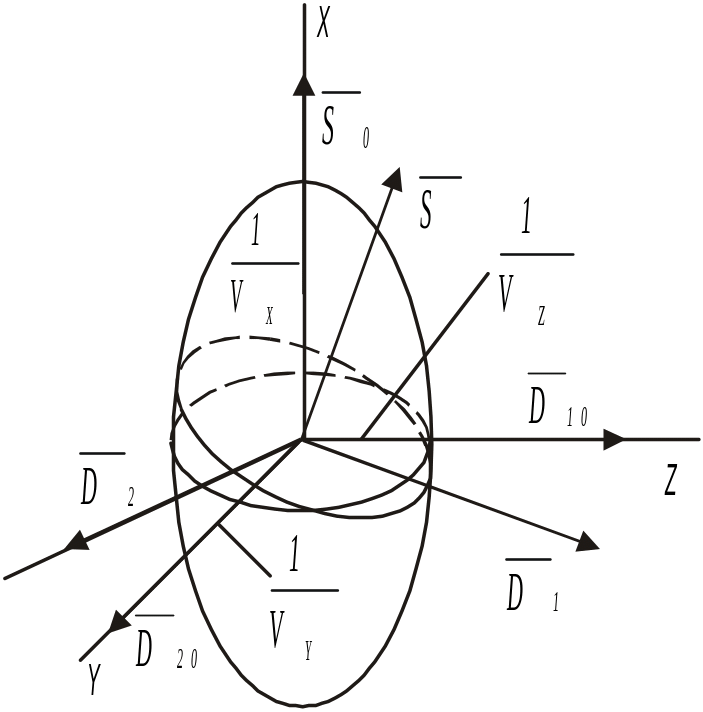

Рис. 12

з которых первый называется лучевым (рис. 11), а второй - волно­вым (рис. 12) эллипсоидами Френеля. Координаты точек на поверх­но­стях эллипсоидов представляют собой с точностью до постоянной зна­чения компонент векторов и соответственно. Отметим, что полуоси лучевого эллипсоида пропорциональны соответствующим главным ско­ростям распространения , , а полуоси волнового эллипсоида об­ратно пропорциональны им.

Рассмотрим решение волнового уравнения Френеля для волны, распространяющейся вдоль одной из координатных осей, например вдоль оси . В этом случае , . Из (2.17) получим

.

Решения этого уравнения очевидны: , . С другой сто­роны, из рассмотрения частных случаев мы ужe знаем, что с главной ско­ростью распространяется волна, поляризованная вдоль оси , со ско­ростью - волна, поляризованная вдоль оси . Из рис. 12 следует, что указанные направления колебаний векторов и совпадают с полу­осями эллипса центрального сечения волнового эллипсоида Френеля плоскостью, ортогональной , т.е. плоскостью . Аналогично для волны, распространяющейся вдоль оси из (2.20) для групповой скоро­сти получим

,

т.е. . Направления колебаний векторов и совпадают с осями и ,т.е. с полуосями эллипса центрального сечения лучевого эллипсоида (см. рис. 11). Рассмотренный алгоритм определе­ния направлений колебания векторов , и , можно распростра­нить и на общий случай положения векторов и в пространстве. Этот алгоритм формулируется следующим образом: для того чтобы опреде­лить направление колебаний векторов при заданном зна­чении вектора распространения луча (волнового фронта) в кри­сталле, необходимо построить центральное сечение лучевого (волно­вого) эллипсоида Френеля плоскостью, ортогональной вектору . Тогда направления колебаний векторов будут совпадать с полу­осями полученного эллипса сечения. Лучевые (фазовые) скорости соот­ветствующих волн будут прямо (обратно) пропорциональны длинам по­луосей.

Указанный алгоритм нагляден (см. рис. 11 и 12) и очень удобен для анализа особенностей распространения световых волн в кристаллах. Подробное доказательство его приведено в работе [2]. Как известно из аналитической геометрии, в любом эллипсоиде общего вида могут быть найдены не более двух центральных сечений, представляющих собой ок­ружность; это означает, что в любом кристалле существуют не более двух направлений , ортогональных соответствующим сечениям, в ко­торых кристалл проявляет себя как изотропная среда. Такие направления называют лучевыми (волновыми) оптическими осями, а соответствующий кристалл - двухосным. При равенстве двух из трех значений главных ди­электрических проницаемостей эллипсоиды Френеля являются эллип­соидами вращения. В этом случае оптические оси вырождаются в одну оптическую ось - ось вращения, а кристалл называется одноосным.